מודל חצי המישור של פואנקרה

קרניים מקבילות במודל חצי המישור של פואנקרה.

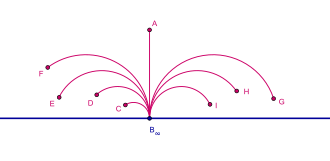
בגאומטריה לא אוקלידית, מודל חצי המישור של פואנקרה הוא חצי המישור העליון, המסומן בדרך כלל $\mathbb {H} =\{\langle x,y\rangle \mid y>0;x,y\in \mathbb {R} \}$, יחד עם המטריקה שמאפיינת אותו, והופכת אותו למודל של גאומטריה היפרבולית דו-ממדית. באופן שקול, מודל חצי המישור העליון של פואנקרה מתואר לעיתים כמישור מרוכב שבו החלק המדומה הוא חיובי.

מודל חצי המישור של פואנקרה נקרא על שם אנרי פואנקרה, אבל המקור שלו הוא בעבודותיו של אאוג'ניו בלטרמי אשר נעזר בו, יחד עם מודל קליין ומודל הדיסק של פואנקרה, כדי להוכיח שהגאומטריה ההיפרבולית היא עקבית אם ורק אם הגאומטריה האוקלידית היא עקבית.

מודל זה הוא קונפורמי, מה שאומר שזוויות בין עקומות כפי שהן נמדדות בנקודת החיתוך שלהן הן בדיוק אותן הזוויות כמו במישור ההיפרבולי האמיתי.

טרנספורם קיילי מספק איזומטריה בין מודל חצי המישור העליון ומודל הדיסק של פואנקרה.

מטריקה

קווים ישרים

המטריקה של המודל על חצי המישור העליון, $\{\langle x,y\rangle \mid y>0\},$, היא:

$(ds)^{2}={\frac {(dx)^{2}+(dy)^{2}}{y^{2}}}$

כאשר s מודד את המרחק לאורך הקו (שעשוי להיות עקום). "הקווים הישרים" במישור ההיפרבולי (גאודזות עבור המטריקה הזאת, כלומר עקומים שממזערים את המרחק בין שתי נקודות) מיוצגים במודל זה באמצעות קשתות מעגליות שפוגשות את ציר ה-x בזוויות ישרות (חצי מעגלים שמרכזיהם נחים על ציר ה-x) בתוספת הקרניים הישרות המאונכות לציר ה-x.

ישנן כמה דרכים שקולות להיווכח בכך שהקו הישר שמחבר בין שתי נקודות A ו-B בחצי המישור העליון הוא תמיד חצי מעגל שאורתוגונלי לציר ה-x: דרך אחת, שעושה שימוש בחשבון הווריאציות, היא פשוט לרשום את פונקציונל האורך של מסילות שמתחילות ב-A ונגמרות ב-B בהתאם למטריקה הנתונה, ואז למצוא את המסלול שממזער את האורך לפי משוואות אוילר-לגראנז'.

דרך שנייה, וברורה יותר קונספטואלית, היא לחשוב על "ישר" של חצי המישור העליון בתור התמונה של נקודה שנעה במהירות קבועה ובכיוון קבוע במישור ההיפרבולי "האמיתי" (לא במודל שמייצג אותו). מכיוון שנקודה נעה כזאת גומעת מרחקים שווים בזמנים שווים, הייצוג של הנקודה במודל חצי המישור העליון (תמונת הנקודה) צריך גם הוא לגמוע מרחקים שווים בזמנים שווים. מכיוון שהמרחקים במודל יחסיים הפוך לקואורדינטה האנכית y, תמונת הנקודה נעה בקצב שיחסי לקואורדינטה האנכית שלה, כך שניתן לחלק את חצי המישור בכללותו לפרוסות שוות-מהירות המקבילות לציר ה-x. המעבר הגיאודזי בין נקודה A לנקודה B מתקבל אז בקלות מעקרון הזמן המינימלי – ניתן לדמות את חצי המישור העליון לתווך אופטי שבו מקדם השבירה יחסי הפוך לקואורדינטה y, ואז שימוש ישיר בחוק סנל מאפשר למצוא את צורת מסלולה של קרן אור. חישוב פשוט מראה שאם $\varphi$ היא הזווית בין כיוון ההתקדמות המקומי של הקרן לאנך, אז $\mathbb {sin} \varphi \cdot n(y)=const\implies {\frac {y}{\mathbb {sin} \varphi }}=const$, וקבוע זה הוא למעשה רדיוס העקמומיות של קשת המעגל. מכיוון ש-$n\rightarrow \infty$ כאשר $y\rightarrow 0$, קשת מעגל זו תמיד חותכת את ציר ה-x – המייצג את "הנקודות באינסוף" – בזוויות ישרות.

חישוב מרחק

אם שתי נקודות ${\textstyle p_{1}}$ ו-${\textstyle p_{2}}$ נחות על ישר היפרבולי (חצי מעגל אוקלידי) אשר חותך את ציר ה-x בנקודות האידיאליות ${\textstyle p_{0}=\langle x_{0},0\rangle }$ ו-${\textstyle p_{3}=\langle x_{3},0\rangle ,}$, המרחק בין ${\textstyle p_{1}}$ ל-${\textstyle p_{2}}$ הוא:

$$\operatorname {dist} (p_{1},p_{2})=\left|\ln {\frac {\|p_{2}-p_{0}\|\|p_{1}-p_{3}\|}{\|p_{1}-p_{0}\|\|p_{2}-p_{3}\|}}\right|.$$

כלומר זהו הערך המוחלט של הלוגריתם הטבעי של היחס הכפול של רביעיית הנקודות $p_{0},p_{1},p_{2},p_{3}$.

מספר מקרים פרטיים פשוטים של נוסחת מרחק זו ראויים לציון. עבור שתי נקודות עם אותה קואורדינטת x המרחק הוא:

$$\operatorname {dist} (\langle x,y_{1}\rangle ,\langle x,y_{2}\rangle )=\left|\ln {\frac {y_{2}}{y_{1}}}\right|=\left|\ln(y_{2})-\ln(y_{1})\right|.$$

ועבור שתי נקודות עם אותה קואורדינטת y המרחק מקיים:

$$\operatorname {dist} \left(\langle x_{1},y\rangle ,\langle x_{2},y\rangle \right)=2\operatorname {arsinh} {\frac {|x_{2}-x_{1}|}{2y}}.$$

נקודות ועקומות מיוחדות

• נקודות אידיאליות (נקודות באינסוף) במודל חצי המישור של פואנקרה הן משני סוגים:

• הנקודות על ציר ה-x, ו-:
• נקודה דמיונית אחת ב-$y=\infty$ שהיא הנקודה האידיאלית אליה כל הקווים הניצבים לציר ה-x מתכנסים.

• קווים ישרים, או גאודזות (הנתיבים הקצרים ביותר בין הנקודות שנחות עליהם) מיוצגים על ידי:

• חצי מעגלים שמרכזם נח על ציר ה-x
• קווים ישרים אנכיים הניצבים לציר ה-x.

• מעגל (עקומה בעל מרחק קבוע מנקודה נתונה) בעל מרכז $(x,y)$ ורדיוס $r$ ייוצג על ידי:

מעגל עם מרכז $(x,y\cosh(r))$ ורדיוס $y\sinh(r)$.

• היפר-מעגל (עקום שווה מרחק מישר נתון, שהוא הציר שלו) מיוצג על ידי:

• קשת מעגל שחותכת את ציר ה-x באותן שתי נקודות אידיאליות כמו חצי המעגל שמייצג את הציר שלו אך בזווית חדה או קהה.
• קו ישר שחותך את ציר ה-x באותה נקודה כמו הקו הישר האנכי שמייצג את הציר שלו, אך בזווית חדה או קהה.

• מעגל גבולי (עקום אשר כל הקווים הנורמליים לו מתכנסים אסימפטוטית באותו כיוון) מיוצג על ידי:

• מעגל המשיק לציר ה-x (אך ללא הנקודה האידיאלית של ההשקה, המייצגת את הנקודה האידיאלית אליה מתכנסים כל הקווים הנורמליים)
• ישר המקביל לציר ה-x, ובמקרה זה מרכז המעגל הגבולי הוא הנקודה האידיאלית ב-$y=\infty$.

היחס למודל הדיסק של פואנקרה

טרנספורם קיילי של חצי המישור העליון לדיסק היחידה. כמוראה באיור, הטרנספורם מעתיק קווים המקבילים לציר ה-x (כאמור לעיל, קווים אלו הם מעגלים גבוליים) למעגלים המשיקים למעגל היחידה, ואת ציר ה-x למעגל היחידה עצמו (מודגשים בצבע צהוב).

טרנספורם קיילי, שהוא סוג של העתקת מביוס, מהווה איזומטריה בין מודל חצי המישור העליון למודל הדיסק של פואנקרה. טרנספורם זה מעתיק את הישר הממשי של חצי המישור העליון (שהוא השפה של מודל חצי המישור) למעגל היחידה (שהוא השפה של מודל הדיסק). מכיוון שהעתקת מביוס מעתיקה מעגלים למעגלים, והיא קונפורמית, הקווים הישרים במודל חצי המישור העליון, אשר הם קשתות מעגל החותכות את הישר הממשי בזוויות ישרות, יועתקו תחת טרנספורם קיילי לקשתות מעגליות החותכות את השפה של מודל הדיסק בזוויות ישרות, בתוספת כל הקטרים של דיסק היחידה. כלומר נקודת המבט של טרנספורם קיילי מספקת מסגרת להבנת קווי הדמיון בין שני המודלים.

ראו גם

• מודל הדיסק של פואנקרה
• גאומטריה היפרבולית

מקורות

• Eugenio Beltrami, Teoria fondamentale degli spazi di curvatura constante,Annali di Matematica Pura ed Applicata, ser II 2 (1868), 232–255
• Henri Poincaré (1882) "Théorie des Groupes Fuchsiens", Acta Mathematica v.1, p. 1. מאמר ראשון בסדרת מאמרים על מודל חצי המישור. עותק מאורכב נגיש באופן חופשי. בעמוד 52 ניתן למצוא תרשים של קשת חצי מעגלית (המייצגת ישר) האופייני למודל.

קישורים חיצוניים

מדיה וקבצים בנושא מודל חצי המישור של פואנקרה בוויקישיתוף

• Upper Half-Plane Model
• Half-plane Model