ויקיפדיה:הכה את המומחה/שאלות במדעים מדויקים/ארכיון 12
| דפי ארכיון של הכה את המומחה - שאלות במדעים מדויקים | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ארכיון כללי | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
דף זה הוא דף ארכיון של דיון או הצבעה שהסתיימו. את המשך הדיון יש לקיים בדף השיחה של הערך או הנושא הנידון. אין לערוך דף זה.
הערכת כמות הגורמים של מקדם בינומי
[עריכת קוד מקור]איך אפשר להראות שמתקיים
עבור כל ראשוני אי־זוגי ?--אדי פ' - שיחה
- זה דורש חישוב זהיר. כצעד ראשון, כתוב את k בבסיס p. עוזי ו. - שיחה 21:13, 22 בדצמבר 2015 (IST)
- איך להמשיך?
- (מוטיבציה לטענה: היא מראה שמתקיים )--אדי פ' - שיחה
- סמן , כאשר היא חבורת אוילר של m (למעשה A הוא הגרעין של ההטלה הטבעית ). אז , ומכיוון ש-A חבורה מסדר , התוצאה נובעת ממשפט לגרנז'. עוזי ו. - שיחה 21:07, 26 בדצמבר 2015 (IST)
- תודה.
- סקיצת הוכחה. המרחב הווקטורי פועל כחבורה על התת־קבוצות בגודל k שלו לפי חיבור. יש תת־קבוצות כאלה. מספיק להוכיח שהסדר של כל מסלול מתחלק ב־. נשים לב שאוסף המייצבים של קבוצה נתונה הוא תת־מרחב וקטורי של , כי כפל בסקלר t הוא חיבור t פעמים.
- טוענים שכמות הווקטורים הבת"ל שמייצבים תת־קבוצה נתונה S בגודל k היא לכל היותר ההערכה ה־p־אדית של k. לכן כמות המייצבים של S היא חזקה של p שהיא לכל היותר , ומכך שגודל המסלול הוא מנת גודל החבורה בכמות המייצבים נובע שגודל כל מסלול מתחלק ב. נותר להוכיח ש, כלומר , וזה נכון.
- איך מנמקים את החלק המוטה בהוכחה?--אדי פ' - שיחה 23:05, 23 בינואר 2016 (IST)
- תודה.
- סמן , כאשר היא חבורת אוילר של m (למעשה A הוא הגרעין של ההטלה הטבעית ). אז , ומכיוון ש-A חבורה מסדר , התוצאה נובעת ממשפט לגרנז'. עוזי ו. - שיחה 21:07, 26 בדצמבר 2015 (IST)
מה עונים האתאיסטים על הטור של פיבונאצ'י ומספר פי?
[עריכת קוד מקור]איך זה נמצא בכל כך הרבה מקומות בטבע ללא יד מכוונת? (חסרה חתימה של השואל)
- .היכן זה נמצא בטבע? למיטב זכרוני הטור היה במקור מודל לתיאור אוכלוסיית ארנבים. כלומר- חישוב תיאורטי מספר הארנבים כפונקציה של הזמן, למרות שבפועל זה לאו דווקא כך.
- .מה בעצם השאלה? אם בטבע פרח ועוד פרח זה שני פרחים ועכבר ועוד עכבר זה שני עכברים (ולא שלושה וגם לא אחד וחצי) וכך הלאה, אזי יש מאחורי זה יד מכוונת ומתבקש שגם האתיאיסטים יקיימו מצוות בעקבות כך? גרי רשף - שיחה 22:06, 24 בדצמבר 2015 (IST)
- די בדיון שמתקיים בויקיפדיה:הכה את המומחה#מה עונים האתאיסטים על הטור של פיבונאצ'י ומספר פי?, אין צורך לדון בשאלה זו בשני מקומות. דוד שי - שיחה 23:50, 24 בדצמבר 2015 (IST)
אני מעונין לקבל כאן תשובה מדעית ושם תשובה פשוטה ―אנונימי לא חתם
- התשובה המדעית היא זו שאמורה להיות יותר פשוטה במקרים כאלה. אבל השאלה אינה מדעית כפי שהוסבר שם. ביקורת - שיחה 12:18, 25 בדצמבר 2015 (IST)
- לא ברור לי הקשר לאתאיזם, אבל הנה תשובה "מדעית".
- יצורים מתמטיים כמו סדרת פיבונאצ'י (ויחס הזהב), פאי או הלוגריתם הטבעי מופיעים בטבע משום שהם תוצאות של תהליכים פשוטים, ולכן נפוצים. סדרת פיבונאצ'י מוגדרת לפי היחס , והיא מופיעה בתהליכים שבהם העתיד תלוי בהווה ובעבר המיידי, או כתוצאה של סידור זוויתי לפי יחס הזהב (הסידור של זרעי חמניה הוא דוגמא מפורסמת - ראה הסבר כאן למשל). פאי מופיע במתמטיקה יותר מאשר בטבע; הוא לא רק היחס בין היקף המעגל לקוטרו, אלא גם נקודת האפס הראשונה של פונקציית הסינוס, ובגלל המבנה של טורי טיילור הוא מתגנב לנוסחת אוילר ודרכה לכל המספרים המרוכבים (שהם דרך טבעית לתאר תופעות פיזיקליות). עוזי ו. - שיחה 12:48, 25 בדצמבר 2015 (IST)
תכנון קואדרטי (quadratic programming)
[עריכת קוד מקור]שלום, אני עובד עם הפונקציה quadprog במטלב שממזערת פונקציות ריבועיות קמורות עם אילוצים לינאריים. איך אני יכול בעזרתה למזער פונקציות ריבועיות קעורות/ למקסם פונקציות ריבועיות קמורות, עם אילוצים לינאריים? תודה! 213.8.204.40 12:44, 25 בדצמבר 2015 (IST)
- אי אפשר למקסם פוקנציה ריבועית קמורה - היא גדלה כשמתרחקים. עוזי ו. - שיחה 12:50, 25 בדצמבר 2015 (IST)
- אבל יש אילוצים (לינאריים במקרה זה), ולכן היא פונקציה רציפה על קבוצה סגורה, אז יש לה מקסימום. 213.8.204.40
- לפונקציה רציפה יש מקסימום על קבוצה קומפקטית; אילוצים לינאריים מגדירים קבוצה סגורה, אבל היא אינה קומפקטית. עוזי ו. - שיחה 13:52, 25 בדצמבר 2015 (IST)
- אני מניח שהאילוצים הלינאריים מגדירים קבוצה חסומה, ולכן קומפקטית. תחת הנחה זאת, איך אני יכול למצוא את המקסימום של פונקציה קמורה בעזרת הפונקציה המובנית של מטלב שמוצאת מינימום של פונקציה קמורה? 213.8.204.40 14:10, 25 בדצמבר 2015 (IST)
- אילוצים לינאריים מגדירים הזזה של תת-מרחב; הוא לא חסום. עוזי ו. - שיחה 20:37, 26 בדצמבר 2015 (IST)
- אני מניח שהאילוצים הלינאריים מגדירים קבוצה חסומה, ולכן קומפקטית. תחת הנחה זאת, איך אני יכול למצוא את המקסימום של פונקציה קמורה בעזרת הפונקציה המובנית של מטלב שמוצאת מינימום של פונקציה קמורה? 213.8.204.40 14:10, 25 בדצמבר 2015 (IST)
- לפונקציה רציפה יש מקסימום על קבוצה קומפקטית; אילוצים לינאריים מגדירים קבוצה סגורה, אבל היא אינה קומפקטית. עוזי ו. - שיחה 13:52, 25 בדצמבר 2015 (IST)
- אבל יש אילוצים (לינאריים במקרה זה), ולכן היא פונקציה רציפה על קבוצה סגורה, אז יש לה מקסימום. 213.8.204.40
"תופעה אינשטיינית" צילום מהיר
[עריכת קוד מקור]מישהו יכול להסביר לי את התופעה שבלינק[1] (מדקה 9:45). איך בדיוק מהירות הצילום משפיעה על התמונה. תודה Meni111 - שיחה 06:47, 29 בדצמבר 2015 (IST)
- הדבר לא מוסבר היטב בסרטון. בהתחלה הוא מסביר שכל תמונה מורכבת מחיבור סדרת תמונות "חשוכות" שמסוכרנות היטב עם פולסים של אור שמאירים את החפץ. האדוות שנראות בתמונה עשויות לנבוע מהתאבכות של רכיבי הצבע השונים ו/או מתבנית מוארה(אנ') שמקורה בחיבור התמונות. המדען טוען שהתמונה מראה היפוך בסדר הזמני של אירועים, דבר שאפשרי בתורת היחסות הפרטית. לי זה נשמע כמו ארטיפקט סטרובוסקופי, והקישור לתורת היחסות מוגזם. ―אנונימי לא חתם
- תודה. אתה אומר שאולי מדובר בהתאבכות+האפקט. אבל אי אפשר לבדוק מה הגורם לזה? לא מכיר היפוך זמנים (איך קוראים לזה באנגלית? אני אשמח לקרוא), אבל גם "מהסוף להתחלה" אני מצפה שתהיה אותה תבנית. כמו שאתה מריץ סרטון מהסוף להתחלה ולא מקבל "נגטיב" אלא את אותה תזוזה, אחורה... תודה Meni111 - שיחה
- כדי להבין מה קורה בניסוי צריך למצוא את המאמר הרלוונטי של הפרופ' (google scholar) ולקרוא את ההסבר על המערכת; הדבר לא מוסבר היטב בסרטון. המדען לא אומר שיש היפוך של כיוון הזמן. הזמן ממשיך לנוע "קדימה" ולא לאחור. הוא מקשר את תוצאת הניסוי שלו לכך שביחסות הפרטית הזמן הוא יחסי לצופה, וכך ייתכן שאירועים המתרחשים בו-זמנית במערכת יחוס אחת, יתרחשו זה אחרי זה במערכת יחוס אחרת (צופה אחר). שינוי כלשהו בסדר הזמנים של אירועים לא יכול להפר קשר סיבתי בינהם. לקריאה נוספת ראה (אנ'). ―אנונימי לא חתם
- היי, גם אם הזמנים שונים בין המערכות, איך זה גורם לכך שיתקבל סידור שונה כל כך של הגלים? תודה Meni111 - שיחה 17:24, 1 בינואר 2016 (IST)
- איך זה יכול שלא? ―אנונימי לא חתם
- היי, גם אם הזמנים שונים בין המערכות, איך זה גורם לכך שיתקבל סידור שונה כל כך של הגלים? תודה Meni111 - שיחה 17:24, 1 בינואר 2016 (IST)
- כדי להבין מה קורה בניסוי צריך למצוא את המאמר הרלוונטי של הפרופ' (google scholar) ולקרוא את ההסבר על המערכת; הדבר לא מוסבר היטב בסרטון. המדען לא אומר שיש היפוך של כיוון הזמן. הזמן ממשיך לנוע "קדימה" ולא לאחור. הוא מקשר את תוצאת הניסוי שלו לכך שביחסות הפרטית הזמן הוא יחסי לצופה, וכך ייתכן שאירועים המתרחשים בו-זמנית במערכת יחוס אחת, יתרחשו זה אחרי זה במערכת יחוס אחרת (צופה אחר). שינוי כלשהו בסדר הזמנים של אירועים לא יכול להפר קשר סיבתי בינהם. לקריאה נוספת ראה (אנ'). ―אנונימי לא חתם
- תודה. אתה אומר שאולי מדובר בהתאבכות+האפקט. אבל אי אפשר לבדוק מה הגורם לזה? לא מכיר היפוך זמנים (איך קוראים לזה באנגלית? אני אשמח לקרוא), אבל גם "מהסוף להתחלה" אני מצפה שתהיה אותה תבנית. כמו שאתה מריץ סרטון מהסוף להתחלה ולא מקבל "נגטיב" אלא את אותה תזוזה, אחורה... תודה Meni111 - שיחה
פירוק לגורמים
[עריכת קוד מקור]- האם אני צודק שפירוק לגורמים של פולינום היא בעיה קלה חישובית (ב-), בעוד שפירוק לגורמים של מספרים היא בעיה קשה חישובית (לא ב-)? אם אני צודק - מה הסיבה להבדל ביניהם?
- האם אני צודק שמציאת שורש של פולינום עם משתנים, ודרגה , כאשר k הוא שלם כלשהו, מעל שדה סופי בגודל ניתנת לביצוע ביעילות (כלומר, בזמן פולינומי ב-n)?
213.8.204.30 20:54, 30 בדצמבר 2015 (IST)
- 1. בפירוק לגורמים של פולינום (מעל הרציונליים) אפשר להעזר בהטלות מודולו מספרים ראשוניים קטנים, ובתוצאות מתורת גלואה ותורת המספרים, כמו משפט פרובניוס. בפירוק לגורמים של מספר שלם אין כלים דומים שיכולים לסייע. עוזי ו. - שיחה 00:48, 31 בדצמבר 2015 (IST)
מורפיזם מתפקטר דרך כל מורפיזם עם גרעין קטן יותר?
[עריכת קוד מקור]יהיו שני הומומורפיזמים של חבורות. נניח שמתקיים. האם תמיד יש הומומורפיזם עבורו ?
ערכי על מוגדרים היטב לפי התנאי, אבל האם אפשר להרחיב את h להומומורפיזם על כל B? --אדי פ' - שיחה 22:43, 30 בדצמבר 2015 (IST)
- ראשית, אפשר לחלק את A ב-ker g, ולהניח ש-g חד-חד-ערכי. קיומו של המורפיזם שאתה מבקש הוא תכונה של C, שנקרא (בהנחה שמדובר בחבורות אבליות) מודול אינג'קטיבי, בדיוק אם קיימת השלמה כזו לכל g:A->B חד-חד-ערכי ולכל f:A->C. דוגמא שבה ההשלמה אינה אפשרית: , כאשר f,g הם השיכונים הטבעיים. עוזי ו. - שיחה 00:53, 31 בדצמבר 2015 (IST)
- תודה. מתברר שאין אף חבורה כזאת. כלומר לכל C יש דוגמה נגדית.
- האם יש סיבה טובה למונח "אובייקט חד־חד־ערכי"? אפשר לראות מודול כזה כפונקציה חח"ע, או שהשם סתם משקף את ההצטמצמות בהגדרה לפונקציות g שהן 1-1? --אדי פ' - שיחה 21:43, 31 בדצמבר 2015 (IST)
- הקשר הרבה יותר מרומז, ובוודאי שאינו מצדיק את התרגום של "מודול אינג'קטיבי" ל"מודול חד-חד-ערכי". אפשר לפרש את התכונה הזו כאפשרות להרים העתקות חד-חד-ערכיות אל המודול עצמו. אם מרשים ל-A,B להיות חבורות אבליות (בלבד), אז כן מקיים את הדרישה. עוזי ו. - שיחה 01:25, 1 בינואר 2016 (IST)
רקורסית שכנים
[עריכת קוד מקור]נתונה לי מטריצה גדולה NXN. אני צריכה למצוא את כל השכנים (כולל האלכסוניים) של הנקודה שהערך שלהם זהה לנקודה, ואת השכנים שלהם (רקורסיה).
- בצורה שהצגת את זה אין לך מה לעשות פה רקורסיה - פשוט תבדקי את שמונת השכנים וזהו.
- אם התכוונת שאת צריכה למצוא אברים כלשהם של המטריצה (לאו דווקא שכנים), אז יש מקום לרקורסיה: תעברי על כל אחד משכנייך באופן רקורסיבי, ותסמני כל תא במטריצה שכבר ביקרת בו (ותעבירי את המטריצה עם הסימונים האלו ברקורסיה, כלומר תדאגי שהפונקציה הרקורסיבית תקבל כקלט מטריצה כזאת). תנאי העצירה הוא שכל שכנייך מסומנים ככאלה שכבר ביקרת בהם. 213.8.204.22 09:22, 2 בינואר 2016 (IST)
אם הבנתי נכון, את בעצם רוצה להתחיל מתא מסוים במטריצה ולמצוא רצף של תאים עם אותו ערך. בפסאדו קוד הזה, האיקס והוואי הם הערכים של הנקודה. יש משתנה כללי List שהוא מבנה נתונים, שבסופו של דבר יכיל את כל הנקודות ששייכות לרצף.
rec(x, y)
- add (x, y) to List
- if x-1>=0 and y-1>=0 and (x-1, y-1) not exist in List
- if (x,y) == (x-1,y-1)
- rec(x-1,y-1)
- if (x,y) == (x-1,y-1)
- if x-1>=0 and (x-1, y) not exist in List
- if (x,y) == (x-1,y)
- rec(x-1,y)
- if (x,y) == (x-1,y)
- if y-1>=0 and (x, y-1) not exist in List
- if (x,y) == (x,y-1)
- rec(x,y-1)
- if (x,y) == (x,y-1)
- if x+1<=N and y+1<=N and (x+1, y+1) not exist in List
- if (x,y) == (x+1,y+1)
- rec(x+1,y+1)
- if (x,y) == (x+1,y+1)
- if x+1<=N and (x+1, y) not exist in List
- if (x,y) == (x+1,y)
- rec(x+1,y)
- if (x,y) == (x+1,y)
- if y+1<=N and (x, y+1) not exist in List
- if (x,y) == (x,y+1)
- rec(x,y+1)
- if (x,y) == (x,y+1)
- if x-1>=0 and y+1<=N and (x-1, y+1) not exist in List
- if (x,y) == (x-1,y+1)
- rec(x-1,y+1)
- if (x,y) == (x-1,y+1)
- if x+1<=N and y-1>=0 and (x+1, y-1) not exist in List
- if (x,y) == (x+1,y-1)
- rec(x+1,y-1)
- if (x,y) == (x+1,y-1)
אפשר לעשות את זה יותר יעיל (תגידי אם את צריכה). כרגע הסיבוכיות היא לא משהו אם באמת משתמשים ברשימה. Badidipedia - שיחה 20:09, 3 בינואר 2016 (IST)
צפיפות של גלידה.
[עריכת קוד מקור]מה הצפיפות ביחחדות של גרם לסמק של גלידה קשה (לא אמריקאית)?
הירח שאין לנוגה
[עריכת קוד מקור]גונבה שמועה לאוזני כי מזג האוויר בנוגה הוא תוצא ישיר של מחסור בירח כגורם מיצב, כדוגמת כדוה"א. האם יש אמת בשמועה או שאגדה היא? אם כן, האם ניתן להרחיב?A_Holy_Bartender - שיחה 19:12, 3 בינואר 2016 (IST)
ניוטון רפסון בהרבה ממדים
[עריכת קוד מקור]שלום, תהי פונקציה חלקה. נניח גם שמטריצת הסיאן, H (של f) מקיימת: (כאשר || מסמן ערך מוחלט). האם תחת הנחות אלה שיטת ניוטון רפסון בהרבה ממדים מתכנסת? או אולי צריך עוד הנחות (למשל, שמטריצת הסיאן מוגדרת חיובית)? 213.8.204.4 08:25, 4 בינואר 2016 (IST)
פונקציה אפינית
[עריכת קוד מקור]האם פונקציה מהצורה (כאשר ) חייבת להיות אפינית? 213.8.204.4 13:31, 4 בינואר 2016 (IST)
- זו פחות או יותר ההגדרה. עוזי ו. - שיחה 14:08, 4 בינואר 2016 (IST)
חידה מתמטית
[עריכת קוד מקור]אותה חידה כמו זו, רק שלאיש הראשון אסור להחליף פתקים אך הוא יכול לענות על שאלה אחת בתשובה של כן/לא והוא חייב לתת תשובה (אפשר להסתכל עליו בתור רובוט). בנוסף, כאן מניחים שהפתקים הוגרלו באופן אקראי, וכך גם המספר אותו צריך האיש השני לחפש, שיוגרל לאחר קבלת התשובה מהראשון.
מה האסטרטגיה הטובה ביותר לקבלת הסיכוי המרבי להצלחה?
יש 100 קופסאות. ההסתברות שקיים מעגל באורך עבור היא . (קומבינטוריקה פשוטה, זה כמובן לא נכון עבור כי אז סופרים מצבים מספר פעמים, אם קיים מעגל באורך של 51 ומעלה הוא היחיד באורכו).
בעזרת קירוב לטור ההרמוני וכללי לוגריתמים מקבלים שההסתברות שקיים מעגל שאורכו גדול או שווה ל-51 הוא בערך שזה בערך 69%.
אם השאלה שהאיש יבחר תהיה "האם קיים מעגל שאורכו גדול או שווה ל-51?" אפשר יהיה להגיע להסתברות של שזה בערך 65%. (אם יש מעגל כזה הוא יפתח 50 תיבות באקראי, אחרת הוא יישם את פתרון החידה המקורית).
האם יש דרך להשיג תוצאה טובה יותר? כגדש - שיחה 15:12, 4 בינואר 2016 (IST)
פונקציה קמורה
[עריכת קוד מקור]תהי פונקציה חלקה, עם מינימום גלובלי. האם f בהכרח קמורה? 213.8.204.4 18:15, 4 בינואר 2016 (IST)
- בעצם מצאתי בסוף דוגמה שלא: . 213.8.204.4 20:30, 4 בינואר 2016 (IST)
- הטענה נכונה בסביבה של נקודת המינימום. עוזי ו. - שיחה 20:40, 4 בינואר 2016 (IST)
פולינומים שמגדירים נקודה
[עריכת קוד מקור]נתונים שני פולינומים p,q ב־n משתנים מעל שדה סגור אלגברית. נניח שיש להם רק אפס משותף אחד, r. האם כל פולינום h שמתאפס בנקודה r ניתן להביע בצורה , עבור פולינומים מתאימים f,g? משפט האפסים אומר רק שיש m עבורו .
(המוטיבציה: להוכיח . אז מספיק להראות שהמכנה הוא אוסף הפולינומים שמתאפסים ב, ולהשתמש במשפט האיזומורפיזם הראשון.)--אדי פ' - שיחה 23:06, 9 בינואר 2016 (IST)
- 1. הטענה הראשונה לא נכונה אפילו בשני משתנים: קח p=x^2 ו-q=y. האפס המשותף היחיד הוא בראשית, והפולינום x, שמתאפס שם, אינו צירוף של p,q.
- 2. ביותר משני משתנים, הטענה הראשונה לא *יכולה* להיות נכונה משום שהיא מבקשת להציג אידיאל מקסימלי על-ידי שני יוצרים.
- 3. האיזומורפיזם נכון, משום שהפתרון היחיד למשוואות הוא x=-1 ו-y=0. עוזי ו. - שיחה 23:38, 9 בינואר 2016 (IST)
- 1. תודה.
- 2. אידיאל מקסימלי של דורש 3 יוצרים? למה?
- 3. בדוגמה , עבור f ההצבה, ובכל זאת
?
- 2. זה נובע ממשפט האידיאל הראשי המוכלל: אידיאל מגובה n אינו יכול להיות מינימלי מעל אידיאל הנוצר על-ידי פחות מ-n אברים. 3. הגרעין נוצר על-ידי שני הפולינומים: ההצבה x=-iy-1 הופכת את המשוואה השניה ללינארית. עוזי ו. - שיחה 02:34, 10 בינואר 2016 (IST)
הגרדיאנט מאונך לקווי הגובה
[עריכת קוד מקור]נתבונן בפונקציה (כאשר בין a לבין x יש מכפלה סקלרית). ידוע כי הגרדיאנט בכל נקודה מאונך לקוי הגובה של f. נתבונן בקו הגובה . יהי . אז בבירור . אולם כי הנחנו . ולכן ז"א שהגרדיאנט אינו מאונך ל x! (בהנחה ו ). איך זה מסתדר? 80.246.137.67 09:04, 11 בינואר 2016 (IST)
- וקטור הגרדיאנט המאונך לקו הגובה הוא זה שיוצא מ-x. בחישוב שהדגמת, אתה מחשב את הזווית עם הוקטור המוזז לראשית - וזו לא אותה זווית. עוזי ו. - שיחה 14:34, 11 בינואר 2016 (IST)
- הבנתי. תודה!
- ומה החישוב הנכון? כלומר, איזה אנך עובר מהראשית לקו הגובה A הנ"ל? 80.246.137.11 18:35, 11 בינואר 2016 (IST)
- בחר נקודה x_0 שבה אתה מעוניין. הזז x_0 לראשית עם קבוצת קווי הגובה: , ובמקרה שלנו . הקבוצה הזו אכן אורתוגונלית לגרדיאנט a. עוזי ו. - שיחה 19:34, 11 בינואר 2016 (IST)
- תודה רבה! 185.32.179.113 10:00, 13 בינואר 2016 (IST)
- בחר נקודה x_0 שבה אתה מעוניין. הזז x_0 לראשית עם קבוצת קווי הגובה: , ובמקרה שלנו . הקבוצה הזו אכן אורתוגונלית לגרדיאנט a. עוזי ו. - שיחה 19:34, 11 בינואר 2016 (IST)
BFS מטלב
[עריכת קוד מקור]נתון לי קטע הקוד הבא, שמחשב מסלול אופטימלי עבור מפה בגודל 5*5 שיש בה מכשולים. אילו שינויים צריך לערוך כדי להפוך את זה לפונקציה שפותרת את אותה הבעיה עבור מפה בגודל N*N כלשהו? ―אנונימי לא חתם
הסרתי מכאן 80 שורות קוד. לשואל: אם אתה מצפה לתגובה מועילה, הראה שאתה עושה מאמץ מינימלי למקד את השאלה. עוזי ו. - שיחה 13:24, 12 בינואר 2016 (IST)
הקוד נדרש בשביל הבנת השאלה, כיוון שהיא מבקשת לערוך את הקוד הנתון. אנסה להעתיק רק שורות רלוונטיות בכל זאת. מה שניסיתי לעשות הוא להפוך את המספר 5 לN בכל מקום שהוא מופיע, ולאפיין את הסקריפט הזה כפונקציה. עדיין לא עזר.
clear all
close all
clc
%%% THIS IS WHERE THE STARTING POSITION %%%
%%% AND GOAL LOCATION ARE DEFINED %%%
startingPosition=[5,5];
goal=[0,5];
%Define the colors for plotting the results
obstacleColor=[1,0,0]; %red
nodeColor=[0,1,0]; %green
expandColor=[0,0,0]; %black
goalColor=[0,0,1]; %blue
pathColor=[0,1,1]; %cyan
%Plot the grid and obstacles
scatter(obstacles(:,1),obstacles(:,2),100,obstacleColor,'filled');
grid ;
axis([0 5 0 5]);
hold on;
%Plot the goal position
scatter(goal(1,1),goal(1,2),100,goalColor,'filled');
%Initialize variables
fringeCount=1; %Used for stepping through the fringe set (keeps track of the current node in the fringe set)
tempCount=1; %Used for expanding the fringe set (keeps track of the end of the fringe set)
%Initialize the fringe set. the structure is:
%fringe(xPosition, yPosition, parentNode)
fringe(fringeCount,:)=[startingPosition,fringeCount];
%This loop executes until the goal is found
while (~((fringe(fringeCount,1)==goal(1,1)) & (fringe(fringeCount,2)==goal(1,2))))
%Plot the current node
scatter(fringe(fringeCount,1),fringe(fringeCount,2),100,nodeColor,'filled');
%Expand the fringe set to the left, right, top and bottom of the current node
for x=-1:1
for y=-1:1
%This is a simple test to ensure that the fringe set isn't
%expanded diagonally as the robot can not move diagonally
if (x*y==0)
%'failsTest' is used to determine when a node can not be
%expanded because it is outside the grid, on an obstacle,
%or it has already been expanded.
failsTest=0;
%'tempNode' is the current node that is trying to be
%expanded
tempNode=[fringe(fringeCount,1)+x,fringe(fringeCount,2)+y, fringeCount];
%Test to see if the node is outside grid
if ( (tempNode(1,1)<0) | (tempNode(1,2)<0) ) | ( (tempNode(1,1)>5) | (tempNode(1,2)>5) )
failsTest=failsTest+1;
end
%If it did not fail the first test, test to see if node is
%already in fringe set.
if (failsTest<1)
for i=1:size(fringe,1)
if (tempNode(1,1)==fringe(i,1)) & (tempNode(1,2)==fringe(i,2))
failsTest=failsTest+1;
end
end
end
%If it did not fail the other tests, test to see if node is
%an obstacle
if (failsTest<1)
for i=1:size(obstacles,1)
if (tempNode(1,1)==obstacles(i,1))&(tempNode(1,2)==obstacles(i,2))
failsTest=failsTest+1;
end
end
end
%If it doesn't fail any tests, add to end of fringe set.
%In breadth first search, nodes are removed from the end of
%the fring set, so to make things easy we add new nodes to
%the end.
if (failsTest<1)
fringe(fringeCount+tempCount,:)=tempNode;
scatter(tempNode(1,1),tempNode(1,2),100,expandColor,'filled');
tempCount=tempCount+1;
end
end
end
end
%Increment to the next node. When you increment, you must also
%decrement tempCount since it is defined as a position in the fringe
%set relative to fringeCount
fringeCount=fringeCount+1;
tempCount=tempCount-1;
pause(5);
end
%Initialize a counter
i=1;
%Trace back through the parent nodes to receover the path
while ~(fringeCount==1)
path(i,:)=[fringe(fringeCount,1),fringe(fringeCount,2)];
fringeCount=fringe(fringeCount,3);
i=i+1;
end
%Add the start position to the path
path(i,:)=startingPosition;
%Plot the path
plot(path(:,1),path(:,2));
scatter(path(:,1),path(:,2),100,pathColor,'filled');
זמן ריצה של יצירה באיחוד קבוצות זרות
[עריכת קוד מקור]שלום,
כתוב בערך איחוד קבוצות זרות שבמקרה של יער של קבוצות זרות, זמן הריצה של יצירה הוא . לכאורה ברור, לפי הפסודו קוד שבערך, שזה אמור להיות להיות . מה אני מפספס כאן?
תודה
- אני מקווה שהתשובה בערך באנגלית סיפקה אותך. תרגיש חופשי לשנות גם אצלנו. (אם יהיה לי זמן אז אולי אני אעשה את זה). Badidipedia - שיחה 19:48, 17 בינואר 2016 (IST)
הגדרת גרף בתורת הגרפים
[עריכת קוד מקור]שלום,
האם גרף מוגדר חד חד ערכית ע"י קבוצת הקודקודים שלו וקבוצת הקשתות, ללא תלות בייצוג הוויזואלי שלו? בפרט, מהערך גרף מישורי קיבלתי את הרושם שהקשתות חייבות להיות מצוירות כקווים ישרים - האם זה נכון, או שגרף שאפשר לצייר אותו במישור באופן שהקשתות הן עקומות שלא נחתכות, הוא גם גרף מישורי? תודה, 31.154.159.174 07:44, 18 בינואר 2016 (IST)
- 1. המושג "גרף" מתייחס בקומבינטוריקה לקודקודים והקשתות. הייצוג הויזואלי אינו רלוונטי. כשרוצים לטפל בייצוג הויזואלי מדברים על "גרף משוכן" וכדומה. 2. גרף מישורי הוא גרף שאפשר לשכן במישור באופן כזה שהקשתות הן עקומות חלקות (לאו דווקא קוים ישרים), שאינן נחתכות. עוזי ו. - שיחה 09:30, 18 בינואר 2016 (IST)
- שתי ההגדרות לגרף מישורי שהוזכרו הן שקולות. --אדי פ' - שיחה 20:57, 18 בינואר 2016 (IST)
התפשטות המרחב
[עריכת קוד מקור]שמעתי שנטען כי המרחב מתפשט ב 70 ק"מ בערך למגה פארסק בכל שניה. כך נראה שגלקסיות מתרחקות מאיתנו בתאוצה כפונקציה של מרחק. אך אם זה נכון, מדוע איננו רואים את המרחב מתפשט בתוך כדור הארץ, בתוך גופינו וכו'?A_Holy_Bartender - שיחה 08:53, 20 בינואר 2016 (IST)
- לפי הקצב שנתת, כדור הארץ כולו מתרחב בחצי מילימטר לשנה. עוזי ו. - שיחה 11:52, 20 בינואר 2016 (IST)
- כיווץ עקב כוחות פנימיים של גוף (חשמלי וכובד) חזק בהרבה מהתרחבות בעקבות ניפוח היקום. כדור הארץ נמצא בשיווי משקל הידרוסטטי בו הכוחות הפנימיים מאזנים את החיצוניים (לחץ נגד כבידה). התרחבות היקום היא הפרעה זניחה ביחס לגדלים אלו. Corvus-TAU - שיחה
- אם החישוב של עוזי ו. הוא נכון (ואני אכן מניח כך) הרי שכמות הזמן שכדור הארץ קיים 4.54 מיליארד שנים, משמעה כי בזמן זה הוא התרחב כ-22700 ק"מ שזה כמעט כפול מקוטרו הנוכחי. אם אקח את המסה הנוזלית הלוהטת מלפני 4.54 מיליארד שנים, וארחיב אותה ברדיוס של 11350 ק"מ הרי שכדוה"א היה צריך להיות יותר מכפול ברדיוסו כיום.A_Holy_Bartender - שיחה 14:09, 20 בינואר 2016 (IST)
- אולי אם יוצאים מתוך הנחה שזהו באמת גיל היקום... ואגב, הקצב שמובא בראשית הערך גיל היקום (ככל הראה עם מקור אמין, לא בדקתי) הוא 67.11 קילומטר בשנייה למיליון פרסק, אז אני מניח שזה קירוב מספיק טוב. חיים ק • שיחה • תרמו לערך הזה • י"ד בשבט ה'תשע"ו • 01:18, 24 בינואר 2016 (IST)
- אם החישוב של עוזי ו. הוא נכון (ואני אכן מניח כך) הרי שכמות הזמן שכדור הארץ קיים 4.54 מיליארד שנים, משמעה כי בזמן זה הוא התרחב כ-22700 ק"מ שזה כמעט כפול מקוטרו הנוכחי. אם אקח את המסה הנוזלית הלוהטת מלפני 4.54 מיליארד שנים, וארחיב אותה ברדיוס של 11350 ק"מ הרי שכדוה"א היה צריך להיות יותר מכפול ברדיוסו כיום.A_Holy_Bartender - שיחה 14:09, 20 בינואר 2016 (IST)
- כיווץ עקב כוחות פנימיים של גוף (חשמלי וכובד) חזק בהרבה מהתרחבות בעקבות ניפוח היקום. כדור הארץ נמצא בשיווי משקל הידרוסטטי בו הכוחות הפנימיים מאזנים את החיצוניים (לחץ נגד כבידה). התרחבות היקום היא הפרעה זניחה ביחס לגדלים אלו. Corvus-TAU - שיחה
- התפשטות המרחב מתקיימת רק כשצפיפות המאסה נמוכה מכדי לבלום אותה. לא רק שכדור הארץ אינו מתפשט, גלאקסייות אינת מתפשטות. אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 22:30, 27 בינואר 2016 (IST)
רזולטנט
[עריכת קוד מקור]- ידוע שהרזולטנט של 2 פולינומים הוא 0 אםם יש שורש משותף לשני הפולינומים. בחלק מהמקומות כתוב שזה נכון רק עבור פולינומים הומוגניים, ובחלק כתוב שזה נכון תמיד. מה הסיבה לסתירה?
- מה הרזולטנט של כמה פולינומים? כלומר, איזה פולינום במקדמים שלהם מתאפס כשיש להם שורש משותף?
213.8.204.77 11:22, 20 בינואר 2016 (IST)
- 1. ראה הערך שלנו רזולטנט - אין צורך להניח שהפולינום הומוגני.
- 2. מצאתי את זה. עוזי ו. - שיחה 12:18, 20 בינואר 2016 (IST)
- תודה!
- בקישור שהפנית אליו, יש התייחסות למשוואות הומוגניות. מה במקרה שהן לא הומוגניות? 213.8.204.77 13:09, 20 בינואר 2016 (IST)
- בדרך כלל אפשר לעבור בין המקרים על-ידי הצבות: אם f(x,y) הומוגני אז f(x,1) הוא פולינום כללי לא הומוגני, ואם g(t) לא הומוגני אז g(x/y) (כפול חזקה מתאימה של y) הוא הומוגני. עוזי ו. - שיחה 13:44, 20 בינואר 2016 (IST)
- הבנתי. תודה!
- בדרך כלל אפשר לעבור בין המקרים על-ידי הצבות: אם f(x,y) הומוגני אז f(x,1) הוא פולינום כללי לא הומוגני, ואם g(t) לא הומוגני אז g(x/y) (כפול חזקה מתאימה של y) הוא הומוגני. עוזי ו. - שיחה 13:44, 20 בינואר 2016 (IST)
האם גם הדרך הבאה לחישוב הרזולטנט של קבוצת פולינומים נכונה: ניקח את 2 הפולינומים הראשונים, ונחליף אותם ברזולטנט שלהם. את הרזולטנט שלהם נחשב על ידי זה שנקבע את כל המשתנים פרט לאחד, ואז פשוט נחשב את הרזולטנט הרגיל של 2 פולינומים במשתנה אחד. קיבלנו עכשיו קבוצת פולינומים קטנה יותר. נחזור על התהליך עד שנקבל קבוצת פולינומים בגודל אחד (כלומר, קבוצה המכילה פולינום יחיד). הפולינום שקיבלנו לבסוף הוא הרזולטנט של קבוצת הפולינומים. האם פתרון זה נכון? 213.8.204.77 15:21, 20 בינואר 2016 (IST)
- אני לא רואה איך זה יעבוד. אם מדובר בפולינומים במשתנה אחד, הרזולטנט של שני הראשונים הוא מספר - ומה עכשיו? עוזי ו. - שיחה 15:53, 20 בינואר 2016 (IST)
- מממ... צודק... 213.8.204.77 17:57, 20 בינואר 2016 (IST)
- אני לא רואה איך זה יעבוד. אם מדובר בפולינומים במשתנה אחד, הרזולטנט של שני הראשונים הוא מספר - ומה עכשיו? עוזי ו. - שיחה 15:53, 20 בינואר 2016 (IST)
חישוב מכפלה בצורה יעילה
[עריכת קוד מקור]נסמן . מהו כפונקציה של b ושל c? כלומר, בהינתן שאנחנו יודעים את b ואת c, מה הדרך היעילה ביותר לחשב את d (כלומר, לחשב אותו בסיבוכיות נמוכה)? 213.8.204.77 11:45, 21 בינואר 2016 (IST)
- בלי ידיעת הפירוק, d אינו מוגדר היטב. אם מניחים שהגורמים a_i ראשוניים, אז d מוגדר היטב אבל חישובו שקול (לפחות במקרה של שני גורמים) לפירוק, וזו כידוע בעיה קשה. עוזי ו. - שיחה 13:32, 21 בינואר 2016 (IST)
שאלה קומבינטורית
[עריכת קוד מקור]כמה מטריצות קיימות מעל עד כדי סדר השורות והעמודות (כלומר, 2 מטריצות שניתן להגיע מאחת לשנייה באמצעות סדרה של פרמוטציות על השורות ו/או העמודות ייחשבו לאותה מטריצה)? עברית - שיחה 18:18, 23 בינואר 2016 (IST)
- אפשר לחשב בעזרת הלמה של ברנסייד: , כאשר הוא מספר המחזורים בתמורה. הפונקציה יוצרת המומנטים של האורך ידועה, אבל מכיוון שכאן מדובר בחזקה של מכפלה, לא הייתי מצפה לתשובה פשוטה יותר. עוזי ו. - שיחה 20:33, 23 בינואר 2016 (IST)
- וואו! לא הייתי מגיע לזה לבד! תודה!! :) עברית - שיחה 21:57, 23 בינואר 2016 (IST)
- כדאי לחשב איברים ראשונים בסדרה ולהכניס אותם כשאילתה ל־OEIS. במקרה דנן.--אדי פ' - שיחה 23:19, 23 בינואר 2016 (IST)
- וואו! לא הייתי מגיע לזה לבד! תודה!! :) עברית - שיחה 21:57, 23 בינואר 2016 (IST)
תנועת "שלולית" הפרפין הנוזלי בנר
[עריכת קוד מקור]תוך כדי הבטה על נר דולק, שמתי לב ללכלוך זעיר (כנראה חתיכת פיח) נעה ממרכז המעגל (הפתילה של הנר) לכיוון "שפת השלולית" וחוזר חלילה...
עם קצת יותר תשומת לב ראיתי שהתנועה פנימה מתרחשת יותר קרוב לקרקעית השלולית בניגוד לתנועה החוצה שמתרחשת קרוב לפני השטח, ואולי היא גם איטית ממנה...
בהנחה שלא דמיינתי או ראיתי איזה מקרה חריג שנבע מעניינים צדדיים שהיו שם, יכול להיות שהתנועה לא הייתה בדיוק הלוך וחזור במסלול בן שני חלקים, אלא כחלק מסליל ארוך (מעין קפיץ שראשו מחובר לסופו בצורת טבעת, כמו הסליל האמצעי למטה בתמונה הראשונה בערך סליל השראה), שאמור בעצם להקיף את הפתילה בסופו של דבר.
ממה נובעת התנועה הזאת בעצם? הפתילה שואבת את הדלק ומה שלא נקלט נפלט חזרה? ואם כן למה השאיבה דווקא מלמטה?
אני מקווה שהובנתי... ![]() תודה, חיים ק • שיחה • תרמו לערך הזה • י"ד בשבט ה'תשע"ו • 01:13, 24 בינואר 2016 (IST)
תודה, חיים ק • שיחה • תרמו לערך הזה • י"ד בשבט ה'תשע"ו • 01:13, 24 בינואר 2016 (IST)
- סביר שמדובר בזרם קונבקציה, ראה (אנ') אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 22:26, 27 בינואר 2016 (IST)
תדר של כוס
[עריכת קוד מקור]ידוע שכדי לפוצץ כוס עם קול יש לכוון אל הכוס רמקול הפולט קול בתדר של הכוס. אך מה זה אומר התדר של הכוס? הרי הכוס תרטוט מכל קול בגלל שכל קול זה אוויר נע שמתנגש בה. מה הופך תדר מסוים למיוחד? תודה Meni111 - שיחה 22:07, 25 בינואר 2016 (IST)
- לכוס יש תדר תהודה. קשה למנוע את זה, שכן לזכוכית יש מידה של אלסטיות, והיא רוטטת בתגובה למכה בתדר שנקבע בעיקר על ידי גובה וקוטר הכוס. קל למצוא בניסוי את תדר התהודה של הכוס - זהו התדר בו הכוס תצלצל אחרי שמקישים בה. דרך נוספת היא הרטבת האצבע והחלקתה על שפת הכוס. זה עובד טוב יותר עם כוסות דקות. אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 22:42, 27 בינואר 2016 (IST)
שאלה בתערובת גזים (כימיה די פשוטה לדעתי)
[עריכת קוד מקור]יש לי שתי סדרות של ניסויים (כל סדרה לגז אחר). בסדרת ניסויים שמים גז במיכל בצפיפות וטמפרטורה מוגדרים היטב ומודדים את הלחץ. כך מקבלים עבור כל זוג של שני לחצים: (כל לחץ עבור גז אחר). עכשיו אני רוצה למצוא אנליטית מה יהיה הלחץ ב נתון של תערובת: שמים חצי מגז A וחצי מגז B (חצי-חצי במסה) במיכל ושואלים מה יהיה הלחץ. האם זה פשוט ממוצע בין P1 לP2? הגזים עצמם לא בדיוק אידאליים, אבל אני יכול להתפשר אם החישוב מסובך מדי לגז אמתי. Corvus,(Nevermore) 13:00, 30 בינואר 2016 (IST)
- ניסוי מחשבתי הורה לי שהתשובה חיובית: נניח ששני המיכלים הזהים בנפחם מופרדים ע"י מחיצה, ואני מסיר את המחיצה. באופן ברור נקבל את הממוצע. נחזיר את המחיצה - הלחץ ישאר זהה, כלומר הממוצע, והתערובת תכיל חצי מכל גז בכל חצי מיכל. אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 22:32, 30 בינואר 2016 (IST)
- אני בספק אם בגזים ראלים נקבל בדיוק את הממוצע. בגזים ראלים, התכונות של תערובות תלויות באינטרקציות הספציפיות בין שני סוגי הגז. באנלוגיה, כשמוסיפים 1L אתנול ל-1L מים לא מקבלים בדיוק 2L של תמיסה. ראו en:Activity coefficient. בברכה, 31.154.161.109 06:55, 31 בינואר 2016 (IST)
- אין תגובות ואין מעבר פאזה. לא הבנתי את הניסוי המחשבתי. הסדרת הניסויים שלי נפח הכלי לא נתון (לא בטוח אם הוא חשוב כי יש לי צפיפות כלומר יחס מסה לנפח). אם אני מצמיד שני כלים בלחצים שונים ומאפשר למחצה בינהם לנוע חופשי הם מגיעים לשווי משקל מכני שבו הלחצים משתווים, אבל הצפיפויות משתנות. אם אני מוריד את המחיצה (הניסוי שאני צריך תכלס) הלחץ הופך למשהו בין P1 המוקרי לבין P2 - ואני לא רואה הוכחה לכך שהלחץ החדש הוא ממוצע חשבוני בין שני הישנים. הוא אמור להיות אותו לחץ בשיווי משקל כשנתתי למחיצה לנוע חופשי. מתייג את משתמש:יורם שורק ומשתמש:Okedem בתקווה לתשובה נחרצת לשאלה ברמת כיתה י'... אם זה חשוב, שני הגזים הם (בטמפרטורות גדולות מספיק בשביל להפוך לגזים, אבל לא מספיק בשביל להתפרק לאטומים). Corvus-TAU - שיחה 13:16, 31 בינואר 2016 (IST)
- זה חייב להיות הממוצע, כי לחץ הוא כוח לשטח הדפנות. סכום הכוחות עובד על פני 2 הדפנות, בהתעלמות משטח המחיצה => ממוצע. כמובן, זה דורש שנפח הכלים יהיה שווה. אם לא שווה => לא ממוצע. אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 15:20, 31 בינואר 2016 (IST)
- לפי השערת אבוגדרו לחץ הגז (בטמפרטורה ונפח נתונים) תלוי במספר החלקיקים בלבד ולא במסה של כל חלקיק. הבדלי הצפיפות בין הגזים הם פשוט היחסים בין המסות המולריות של החומרים. אין SiO2 גזי אבל אילו היה הייתה המסה המולרית בערך 60 לעומת 18 במים כך ש"חצי חצי במסה" פירושו תערובת ביחס מולרית בערך 1:3 לטובת המים. יורם שורק - שיחה 18:29, 31 בינואר 2016 (IST)
- למה אין SiO2 גזי? בערך צורן דו-חמצני נותנים נקודת רתיחה של כ2000 קלווין. קטן עלי (אני מדבר על סדרי גודל של כ-5,000-20,000K). הניסוי שלי לא מתבצע במקרה המשעמם של כדור הארץ. לעניינו- אין לי נפח כלי מוגדר. למעשה יש לי תוכנה שבנויה על משוואות מצב במקרים קיצוניים, שהיא מקבלת כקלט T וצפיפות ופולטת לחץ. בעיה איתה שהיא בנויה כך שכל פעם שולפת חומר אחד. ובמציאות אני מעוניין בתערובת. אני יודע שהחישוב יוצא גס מעט, אבל גם ככה מדובר בהערכה תאורטית בלבד. אז לפי מה שאתה אומר אם אני דורש יחס חצי-חצי במסה אז הלחץ של התערובת הוא כאשר הmים זה מסות מולקולת גז א' וגז ב'. כלומר סוג של ממוצע משוכלל. הבנתי נכון? Corvus-TAU - שיחה 20:24, 31 בינואר 2016 (IST)
- אכן יש בערך נקודת רתיחה אבל לא ברור מה מתרחש מעליה. לדעתי פשוט אטומיזציה. האמת היא שהשאלה מסקרנת. חיפשתי בספרות ובמאמר הזה בעמוד 515 אכן מצאתי את ארבעת המילים ”gaseous SiO2 does exist” אבל לא מדובר על נידוף ברתיחה אלא על התזה באמצעות פלזמה. אשר לנוסחה שכתבת: היא כנראה נכונה (בתנאי שהיצור המוזר שהעברנו איכשהו לגז מתנהג דומה לגז אידאלי). יורם שורק - שיחה 21:18, 31 בינואר 2016 (IST)
- המנחה שלי מתנגדת בתוקף להנחת הגז האידאלי במצבים עם צפיפות לחץ וטמפרטורה כאלה גבוהים... אז כנראה צריך להתחכם יותר. Corvus-TAU - שיחה 15:58, 1 בפברואר 2016 (IST)
- אכן יש בערך נקודת רתיחה אבל לא ברור מה מתרחש מעליה. לדעתי פשוט אטומיזציה. האמת היא שהשאלה מסקרנת. חיפשתי בספרות ובמאמר הזה בעמוד 515 אכן מצאתי את ארבעת המילים ”gaseous SiO2 does exist” אבל לא מדובר על נידוף ברתיחה אלא על התזה באמצעות פלזמה. אשר לנוסחה שכתבת: היא כנראה נכונה (בתנאי שהיצור המוזר שהעברנו איכשהו לגז מתנהג דומה לגז אידאלי). יורם שורק - שיחה 21:18, 31 בינואר 2016 (IST)
- למה אין SiO2 גזי? בערך צורן דו-חמצני נותנים נקודת רתיחה של כ2000 קלווין. קטן עלי (אני מדבר על סדרי גודל של כ-5,000-20,000K). הניסוי שלי לא מתבצע במקרה המשעמם של כדור הארץ. לעניינו- אין לי נפח כלי מוגדר. למעשה יש לי תוכנה שבנויה על משוואות מצב במקרים קיצוניים, שהיא מקבלת כקלט T וצפיפות ופולטת לחץ. בעיה איתה שהיא בנויה כך שכל פעם שולפת חומר אחד. ובמציאות אני מעוניין בתערובת. אני יודע שהחישוב יוצא גס מעט, אבל גם ככה מדובר בהערכה תאורטית בלבד. אז לפי מה שאתה אומר אם אני דורש יחס חצי-חצי במסה אז הלחץ של התערובת הוא כאשר הmים זה מסות מולקולת גז א' וגז ב'. כלומר סוג של ממוצע משוכלל. הבנתי נכון? Corvus-TAU - שיחה 20:24, 31 בינואר 2016 (IST)
- לפי השערת אבוגדרו לחץ הגז (בטמפרטורה ונפח נתונים) תלוי במספר החלקיקים בלבד ולא במסה של כל חלקיק. הבדלי הצפיפות בין הגזים הם פשוט היחסים בין המסות המולריות של החומרים. אין SiO2 גזי אבל אילו היה הייתה המסה המולרית בערך 60 לעומת 18 במים כך ש"חצי חצי במסה" פירושו תערובת ביחס מולרית בערך 1:3 לטובת המים. יורם שורק - שיחה 18:29, 31 בינואר 2016 (IST)
- זה חייב להיות הממוצע, כי לחץ הוא כוח לשטח הדפנות. סכום הכוחות עובד על פני 2 הדפנות, בהתעלמות משטח המחיצה => ממוצע. כמובן, זה דורש שנפח הכלים יהיה שווה. אם לא שווה => לא ממוצע. אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 15:20, 31 בינואר 2016 (IST)
- אין תגובות ואין מעבר פאזה. לא הבנתי את הניסוי המחשבתי. הסדרת הניסויים שלי נפח הכלי לא נתון (לא בטוח אם הוא חשוב כי יש לי צפיפות כלומר יחס מסה לנפח). אם אני מצמיד שני כלים בלחצים שונים ומאפשר למחצה בינהם לנוע חופשי הם מגיעים לשווי משקל מכני שבו הלחצים משתווים, אבל הצפיפויות משתנות. אם אני מוריד את המחיצה (הניסוי שאני צריך תכלס) הלחץ הופך למשהו בין P1 המוקרי לבין P2 - ואני לא רואה הוכחה לכך שהלחץ החדש הוא ממוצע חשבוני בין שני הישנים. הוא אמור להיות אותו לחץ בשיווי משקל כשנתתי למחיצה לנוע חופשי. מתייג את משתמש:יורם שורק ומשתמש:Okedem בתקווה לתשובה נחרצת לשאלה ברמת כיתה י'... אם זה חשוב, שני הגזים הם (בטמפרטורות גדולות מספיק בשביל להפוך לגזים, אבל לא מספיק בשביל להתפרק לאטומים). Corvus-TAU - שיחה 13:16, 31 בינואר 2016 (IST)
- אני בספק אם בגזים ראלים נקבל בדיוק את הממוצע. בגזים ראלים, התכונות של תערובות תלויות באינטרקציות הספציפיות בין שני סוגי הגז. באנלוגיה, כשמוסיפים 1L אתנול ל-1L מים לא מקבלים בדיוק 2L של תמיסה. ראו en:Activity coefficient. בברכה, 31.154.161.109 06:55, 31 בינואר 2016 (IST)
וריאציה על gradient descent
[עריכת קוד מקור]יהיו (ידוע ש f חלקה, אבל היא לא בהכרח קמורה). נרצה למצוא נקודה כך ש (נניח ש-x אינו מינימום מקומי של f). איך ניתן לעשות זאת?
חשבתי בהתחלה לקחת (עם אלפא מתאים), כמו ב gradient descent, אבל אז הבנתי שזה לא יעבוד - למשל, אם x נקודת אוכף. מה לעשות?
ניסוח נוסף לאותה שאלה: gradient descent עוסק במציאת מינימום גלובלי לפונקציה קמורה. איך ניתן למצוא מינימום כלשהו (לאו דווקא גלובלי) לפונקציה חלקה שלא מובטח שהיא קמורה? 80.246.136.89 18:21, 31 בינואר 2016 (IST)
פירוק Cholesky
[עריכת קוד מקור]האם עבור מטריצה A מתקיים שיש לה פירוק Cholesky אםם היא הרמיטית ו- positive definite? (כלומר, אני יודע שכיוון אחד נכון, השאלה היא האם שני הכיוונים נכונים) עברית - שיחה 19:30, 2 בפברואר 2016 (IST)
- כל מטריצה מהצורה (כאשר B מרוכבת והפיכה) היא בוודאי הרמיטית וחיובית לחלוטין. בכיוון ההפוך, אם A הרמיטית אז היא לכסינה אורתוגונלית; אבל אם היא חיובית לחלוטין הערכים העצמיים שלה ממשיים וחיוביים, ולכן יש להם שורש ממשי וחיובי; מן השורש הזה אפשר בקלות לבנות פירוק מהצורה . עוזי ו. - שיחה 23:22, 2 בפברואר 2016 (IST)
- תודה! עברית - שיחה 19:50, 3 בפברואר 2016 (IST)
הוכחה לא הסתברותית בגרפים
[עריכת קוד מקור]שלום,
אם יש לנו גרף בו (כאשר מספר טבעי כלשהו) ועבור כל שני קודקודים שאינם שכנים מתקיים , איך אפשר להוכיח שהדרגה הממוצעת של הגרף היא לפחות k?
ראיתי דרך ההסתברותית, ואשמח לראות פתרון בדרך "רגילה" (ע"י ספירת קשתות, הנחה בשלילה, אינדוקציה וכו) שאינה מכילה שיקולים הסתברותיים.
תודה רבה
מעלית
[עריכת קוד מקור](הועבר מוק:הכה) יש לי מעלית במנוחה. מתקרת המעלית תלויה גלגלת. מהגלגלת תלויות משני צדדיו של חוט אבן גדולה ואבן קטנה. מטבע הדברים האבן הקטנה תימשך למעלה על ידי החוט, והאבן הגדולה תמשוך את החוט כלפי מטה. כעת אני מאיץ את המעלית כלפי מטה, בתאוצה הגדולה מתאוצת הכובד. כלומר יש לי בתוך המעלית כוח מדומה הפועל כלפי מעלה. האם ישתנה משהו מבחינת הגלגלת? בלנק - שיחה 17:57, 6 בפברואר 2016 (IST)
- תבנית:קימוט מצח זה לא שייך למדעים מדוייקים? או שאתה מחפש משהו פילוסופי? אילן שמעוני - שיחה החיים הם גבול של אתה פופולר 18:13, 6 בפברואר 2016 (IST)
- צודק, לא הייתי פה הרבה זמן
 . אעביר. בלנק - שיחה 18:23, 6 בפברואר 2016 (IST)
. אעביר. בלנק - שיחה 18:23, 6 בפברואר 2016 (IST)
- צודק, לא הייתי פה הרבה זמן
- אפשר לפרק את הסיפור לשניים. שני הגופים הקשורים בחוט הם מעין מתקן המכפיל את התאוצה בקבוע (M-m)/(M+m), כאשר M,m הן המסות של שני הגופים. כשהמעלית מואצת, זה כאילו הוספת לתאוצת הכובד את תאוצת המעלית, ומתקן ההכפלה שלנו פועל גם לפני וגם אחרי התוספת. עוזי ו. - שיחה 20:09, 6 בפברואר 2016 (IST)
- אז לפי זה עכשיו "תאוצת הכובד המעודכנת" פועלת כלפי מעלה, ולכן החפץ הכבד יותר יעלה למעלה והקל יותר ירד למטה, לא? בלנק - שיחה 09:14, 7 בפברואר 2016 (IST)
- תלוי בכיוון התאוצה של המעלית... אם היא עולה, g הופך להיות g+a, ואם היא יורדת -- g-a. החפץ הכבד יותר יפול בכיוון של תאוצת הכובד המשולבת. עוזי ו. - שיחה 11:37, 7 בפברואר 2016 (IST)
- תודה. בלנק - שיחה 13:25, 7 בפברואר 2016 (IST)
- תלוי בכיוון התאוצה של המעלית... אם היא עולה, g הופך להיות g+a, ואם היא יורדת -- g-a. החפץ הכבד יותר יפול בכיוון של תאוצת הכובד המשולבת. עוזי ו. - שיחה 11:37, 7 בפברואר 2016 (IST)
- אז לפי זה עכשיו "תאוצת הכובד המעודכנת" פועלת כלפי מעלה, ולכן החפץ הכבד יותר יעלה למעלה והקל יותר ירד למטה, לא? בלנק - שיחה 09:14, 7 בפברואר 2016 (IST)
האם תכונת התרחבות החומרים בקפיאה אינה נכונה לכל החומרים? אינג. יונה ב. - שיחה - הבה נכחילה 10:55, 8 בפברואר 2016 (IST)
- לא, דווקא הרוב מתכווץ. Corvus-TAU - שיחה 11:04, 8 בפברואר 2016 (IST)
- אוקיי. אינג. יונה ב. - שיחה - הבה נכחילה 13:01, 8 בפברואר 2016 (IST)
- ראה האנומליה של המים. דניאל 14:15, 8 בפברואר 2016 (IST)
מספר אלגברי אי רציונלי
[עריכת קוד מקור]נניח שיש לי קירוב טוב למספר אלגברי אי רציונלי. (נניח- קיבלתי פולינום ומצאתי את השורשים באופן מקורב). אני רוצה למצוא הצגה יותר נוחה שלו, אך ורק באמצעות מספרים רציונלים וסימן השורש.
- א. האם תמיד קיימת הצגה כזאת? (נראה לי די ברור שכן, אני רק מוודא)
- ב. האם יש שיטה מתמטית לעשות את זה?
- ג. האם יש אתר או תוכנה שאתם מכירים שעושה את זה? תודה מראש: בלנק - שיחה 16:51, 14 בפברואר 2016 (IST)
- אין הצגה כזו תמיד. המקרה המוכר ביותר הוא השורש של . ראה פתרון באמצעות רדיקלים. עד מעלה רביעית קיימת הצגה כזו תמיד לפי נוסחה ידועה. ממעלה חמישית ומעלה יש פולינומים שלשורשים שלהם אין הצגה. דניאל 17:05, 14 בפברואר 2016 (IST)
- קירוב רציונלי תמיד קיים: קח את הפיתוח העשרוני של המספר שלך עד למקום שתבחר (בו הקירוב יהיה מספיק טוב), תקצוץ את הזנב ותקבל מספר רציונלי. אבל אני מניח שלא לזה אתם מתכוון. אני מניח שבהוצאת שורש אתה מתכוון לשורש מכל סדר ולא רק לשורש ריבועי. במקרה זה, משפט גלואה (ראה תורת גלואה) אומר שבאופן כללי אין הצגה נוחה כזו, כלומר: לפולינום כללי אין ביטוי כללי למספר שמאפס אותו שכולל רק ארבע פעולות החשבון + הוצאת שורש על קבוצת מקדמי הפולינום איחוד עם קבוצת המספרים הרציונליים. MathKnight-at-TAU ✡ שיחה 17:07, 14 בפברואר 2016 (IST)
- תודה רבה לשניכם (מתנייט, שתי ההנחות שלך נכונות), החכמתי, אבל לא בדיוק לזה התכוונתי. לא התכוונתי לשיטה אחרת להוציא שורש לפולינום, אלא לשיטה להגיע מהקירוב העשרוני להצגה אלגברית מדוייקת (במידה וקיימת). בלנק - שיחה 20:51, 14 בפברואר 2016 (IST)
- ושאלה נוספת שעלתה לי: האם יש איזה שהם מספרים אלגבריים שאי אפשר להציג באמצעות ארבעת פעולות החשבון ושורש שיש להם "שם"? כמו פיי או e? כלומר מספרים שמוגדרים באמצעות הוצאת שורש מפולינום? בלנק - שיחה 20:51, 14 בפברואר 2016 (IST)
- נתון מספר ממשי a. אם רצונך למצוא מספר רציונלי קרוב ל-a עם מכנה קטן ככל האפשר, הדרך לעשות זאת היא למצוא סדרת הקירובים של a באמצעות שברים משולבים. שאלה טבעית אחרת היא לנסות לקרב את a באמצעות שלם אלגברי. אם תקבע מראש את המעלה n (אני הייתי בוחר n=2), אפשר להציג את בתור צירוף לינארי בעל מקדמים שלמים קטנים של החזקות (אני מניח שאלגוריתם LLL (אנ') הוא הכלי המתאים).
- לשאלה השניה - אתה שואל על מספרים אלגבריים "[שלא] כמו פיי או e". מספר אלגברי אפשר לזהות באמצעות הפולינום שלו, ולכן אין צורך לתת להם שמות (ואני לא מכיר כאלה, חוץ אולי מיחס הזהב). עוזי ו. - שיחה 21:46, 14 בפברואר 2016 (IST)
- הנה סקירה טובה של הנושא, וכלי ממוחשב שיעשה כל מה שרצית ויותר. עוזי ו. - שיחה 21:51, 14 בפברואר 2016 (IST)
- קירוב רציונלי תמיד קיים: קח את הפיתוח העשרוני של המספר שלך עד למקום שתבחר (בו הקירוב יהיה מספיק טוב), תקצוץ את הזנב ותקבל מספר רציונלי. אבל אני מניח שלא לזה אתם מתכוון. אני מניח שבהוצאת שורש אתה מתכוון לשורש מכל סדר ולא רק לשורש ריבועי. במקרה זה, משפט גלואה (ראה תורת גלואה) אומר שבאופן כללי אין הצגה נוחה כזו, כלומר: לפולינום כללי אין ביטוי כללי למספר שמאפס אותו שכולל רק ארבע פעולות החשבון + הוצאת שורש על קבוצת מקדמי הפולינום איחוד עם קבוצת המספרים הרציונליים. MathKnight-at-TAU ✡ שיחה 17:07, 14 בפברואר 2016 (IST)
מכפלה טנזורית 0 פירושה מאפסים זרים
[עריכת קוד מקור]יהיו M ,N שני מודולים נוצרים סופית מעל חוג חילופי. נניח שהאידיאל הוא אמיתי. למה מתקיים ? (ראיתי הסבר מעורפל, נוסח "הטל למודול מתאים כדי לקבל העתקה שאינה אפס, ולפי האוניברסליות סיימנו".)--אדי פ' - שיחה 23:58, 16 בפברואר 2016 (IST)
- השאלה נענתה כאן.--אדי פ' - שיחה 22:16, 24 בפברואר 2016 (IST)
לפי עקרון פרמה האור עובר במסלול הקצר ביותר. נניח שהאור נמצא כעת בנקודה A והוא עתיד לפגוע במראה ואז לשנות כיוון ולהגיע לנקודה B - ברור שהמסלול מ-A ל-B (בקו ישר, ובלי לעבור דרך המראה) קצר יותר. למה אם כן הוא עובר דרך המראה? (חשבתי על זה שהאור "לא יודע" שיהיה מראה, אבל אז מה הרעיון של החוק? חשבתי גם שאולי החוק נכון רק עבור A ו B קרובות במידה אינפיניטסימלית, אבל זה לא נשמע כך מניסוח החוק בערך עקרון פרמה). עברית - שיחה 17:52, 21 בפברואר 2016 (IST)
- מה שמדובר פה זה מבין על המסלולים האפשריים שכן משתקפים דרך המראה. כמובן שלעבור ישירות זה יוצר קצר. אבל אם שואלים מה המסלול שכן יעבור דרך מראה, עקרון פרמה ייתן את התשובה הנכונה. eman • שיחה • ♥ 19:28, 21 בפברואר 2016 (IST)
- ואם אין מראה אלא מנסרה ושתי עדשות? התשובה היא שהחוק הוא מקומי (כפי שמשתמש:עברית מציע), וזה צריך להיות ברור מהערך. עוזי ו. - שיחה 20:30, 21 בפברואר 2016 (IST)
- לא. החוק הוא לא מקומי. החוק מדבר על אילוץ, ופשוט האילוץ יכול להשתנות. פעם זה החזרה במראה, פעם זה מעבר בין תווכים וכו. eman • שיחה • ♥ 22:59, 21 בפברואר 2016 (IST)
- ואם אין מראה אלא מנסרה ושתי עדשות? התשובה היא שהחוק הוא מקומי (כפי שמשתמש:עברית מציע), וזה צריך להיות ברור מהערך. עוזי ו. - שיחה 20:30, 21 בפברואר 2016 (IST)
חלקי הכליה
[עריכת קוד מקור]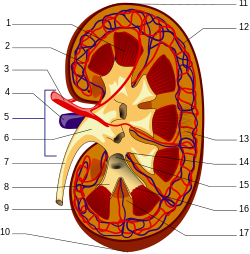
מסתבר שקובץ:Riñon heb.JPG היה במקורו הז"י, ואם כן גם התרגום שלו הוא הז"י (עד כאן, אני מקווה שאני לא טועה).
יש כמה קבצים טובים בויקישיתוף, ומביניהם קובץ:KidneyStructures PioM.svg נראה לי הכי טוב (מוצג משמאל), גם אם לא ברור לי כמה הוא מדויק.
כך או כך, אני מחפש תרגום לתיאורים באנגלית, שלא קיימים בעברית (שלא לדבר על העובדה שיש שתי רשימות: אחת בקובץ ה-SVG המצורף, ואחת בקובץ ה-PNG, והן קצת שונות זו מזו) הנה מה שיש לי בינתיים, לפי הערך כליה:
1. פירמידות הכליה 2. עורק כליה בין־אונתי? 3/4. עורק/וריד הכליה 5. ? 6. אגן הכליה 7. שופכן 8. גביע כליה משני 9. קופסית הכליה 10. קצה הכליה התחתון? 11. קצה הכליה העליון? 12. וריד כליה בין־אונתי? 13. נפרון 14. גביע כליה משני? 15. גביע כליה ראשי 16. פתחת הכליה? 17. עמוד כליה.
התוכלו לחוות דעתכם? תודה מראש, נדב ס. • שיחה 09:33, 22 בפברואר 2016 (IST)
זמן ריצה במכונת טיורינג
[עריכת קוד מקור]אהלן,
אם יש למ"ט קלט והמכונה רצה לכל היותר צעדים, אז למה זה נחשב זמן ריצה אקספוננציאלי? לכאורה זה יותר כי בסיס החזקה הוא משתנה ואינו קבוע (כמו בהגדרה של אקספוננט).
תודה
- זה באמת לא נחשב זמן ריצה אקספוננציאלי (אלא סופר-אקספוננציאלי: מהיר יותר מכל ). עוזי ו. - שיחה 02:36, 26 בפברואר 2016 (IST)
- אני רואה עכשיו לפי וולפראם אלפא ש- גדל הרבה יותר מהר מ-, אז זה כן אקספוננציאלי (ע"פ ההגדרה ). האם יש איזוהי דרך מתמטית פשוטה להוכיח את הנ"ל (ש- )?
- רב תודות
- זה עניין של הגדרות, אבל לרוב נחשב סופר-מעריכי. לשאלתך השנייה:
- ולכן:
- דניאל 12:15, 26 בפברואר 2016 (IST)
- אני רואה עכשיו לפי וולפראם אלפא ש- גדל הרבה יותר מהר מ-, אז זה כן אקספוננציאלי (ע"פ ההגדרה ). האם יש איזוהי דרך מתמטית פשוטה להוכיח את הנ"ל (ש- )?
בועות סבון
[עריכת קוד מקור]מהסתכלות בתמונות באינטרנט ראיתי שבחלק מהתמונות כל הבועות שמשיקות זו לזו מקיימות שאף אחת מהן אינה עגולה, ואילו בתמונות אחרות כל הבועות הן עגולות. מהעובדה שלא נתקלתי באף תמונה שבה חלק מאלה שמשיקות לאחרות הן עגולות וחלק לא - אני מסיק שזה תלוי בדרך יצירת הבועה או משהו כזה... בנוסף, בחלק מהתמונות (כאשר הבועות אינן עגולות) רואים שאין רווח בין בועות משיקות ובחלקן (כאשר הבועות עגולות) יש "רווח" בין בועות משיקות (בגלל העיגול). אגב, מניסוי בבית הבועות יצאו לי לא עגולות.
במה זה תלוי? למה בחלק מהתמונות הבועות הן כאלה ובחלק הן אחרות? 213.8.204.30 22:25, 2 במרץ 2016 (IST)
- אני משער שמדובר במשקל "קליפת" הבועה ביחס לאוויר שבתוכה, צריך להתקיים יחס מדוייק מאד כדי שהבועות לא תילחצנה כלפי מטה לתוך הכדור וכדומה. ביקורת - שיחה 22:51, 2 במרץ 2016 (IST)
- תודה! בנוסף, אתה יודע מה אני צריך לעשות כדי שגם לי בבית ייצאו בועות עגולות? 213.8.204.69 08:38, 5 במרץ 2016 (IST)
- אני לא יודע, כדאי לך להעביר את כל הפסקה הזו לויקיפדיה:הכה את המומחה הרגיל, שהרבה יותר אנשים נחשפים אליו ומגיבים. מדי פעם מתפרסמים באתרים שונים "מתכונים" לבועות סבון. אני מניח שחיפוש המילים הללו יביא לתוצאות סבירות. ביקורת - שיחה 21:15, 5 במרץ 2016 (IST)
- תודה! בנוסף, אתה יודע מה אני צריך לעשות כדי שגם לי בבית ייצאו בועות עגולות? 213.8.204.69 08:38, 5 במרץ 2016 (IST)
פונקצייה יוצרת מומנטים ופונקציה אופיינית של משתנה מקרי
[עריכת קוד מקור]למומחה שלום, בערך על פונקציה אופיינית כתוב "בניגוד לפונקציה יוצרת מומנטים, הפונקציה האופיינית תמיד קיימת וממנה ניתן לקבל את פונקציית צפיפות ההסתברות ואת המומנטים או להסיק על אי קיומם". נשאלת השאלה - מה אני "רואה" על הפונקציה שממנו אני מסיק שאין להתפלגות מומנטים? היא לא גזירה אינסוף פעמים? ה"מומנטים" שאמורים להתקבל מהנוסחה יוצאים מדומים/מרוכבים? זאת ועוד, אם הפונקציה גזירה אינסוף פעמים אבל לא אנליטית (כלומר, התפלגות שהתמרת פורייה שלה היא פונקציה דוגמת ) המומנטים הם הנגזרות של הפונקציה או שהם לא קיימים?
תודה, Eyalweyalw - שיחה 11:44, 11 במרץ 2016 (IST)
אם אינסוף אחד כלול באחר, האם זה אומר שהוא "קטן יותר"?
[עריכת קוד מקור]מה יש יותר: מספרים מ1 עד 2 או מספרים מ0 עד 10? מצד אחד כל אחד מהם הוא אינסוף "מאותו סדר גודל" ואם מכפילים אינסוף במספר סופי (10), אז האינסוף לא גדל. אבל מצד שני, הקטע בין 1 ל2 כלול בקטע מ0 עד 10 כלומר כל מספר בין 1 ל2 חייב להיות שייך לקבוצה בין 0 ל10, אבל לא ליהפך. ככה שהאינסוף השני גדול יותר. איך מיישבים את הסתירה?
- ראה את הערך עוצמה אינסופית. לקבוצות אינסופיות יכולות להיות תת-קבוצות חלקיות ממש (כלומר, לא שוות) בעלות אותה עוצמה (כלומר: אותה כמות איברים). זה נוגד את האינטואיציה כי זה לא נכון לקבוצות סופיות. למעשה, מאפיין זה של קבוצה אינסופית יכול לשמש כהגדרה לקבוצה אינסופית (קבוצה היא אינסופית אם קיימת לה תת-קבוצה חלקית ממש שוות עוצמה). MathKnight ✡ (שיחה) 14:33, 12 במרץ 2016 (IST)
- קח דוגמה יותר פשוטה: קבוצת כל המספרים הטבעיים . יש לתת קבוצה חלקית ממש, קבוצת כל המספרים הזוגיים. לכאורה, ברור שיש יותר מספרים טבעיים מאשר זוגיים, אבל עדיין - קבוצת המספרים הטבעיים וקבוצת המספרים הזוגיים הן שוות עוצמה. למה? כי לכל מספר טבעי ניתן להתאים מספר זוגי כך שההתאמה היא חד-חד-ערכית ועל. כלומר: ניתן לבנות פונקציה בין שתי הקבוצות כך שלכל איבר מאחת מהן מתאים בדיוק איבר אחד בשנייה, כך שהתמונה מכסה את כל הטווח (הקבוצה השנייה) וגם לא שולחת שני איברים מהמקור לאותו איבר בטווח. מה שנקרא: התאמה 1-1 או בייקציה bijection. בקבוצות סופיות קיום התאמה 1-1 חח"ע ועל אפשרי רק כאשר הן שוות עוצמה, כלומר: בעלות אותו מספר איברים. MathKnight ✡ (שיחה) 14:38, 12 במרץ 2016 (IST)
- זה הפרדוקס של גלילאו. עוזי ו. - שיחה 18:44, 12 במרץ 2016 (IST)
- מה שאתם אומרים מעניין. נניח ניסוי מחשבתי שבו ישנה מוכנה המגרילה מספרים פסיידו-אקראיים בין 0 ל10. ומונה הסופר את כמות הפעמים שיצא מספר בין 0 ל10 ומונה שני שסופר את מספר הפעמים שיצא מספר בין 1 ל2. ברור שהמונה הראשון יציג תמיד מספר גדול יותר מהמונה השני, כי הקבוצה השניה היא תת קבוצה בראשונה. האם זה לא מוכיח שיש יותר מספרים בין 0 ל10 מאשר בין 1 ל2?
- לא, למה. זה מוכיח שבהתפלגות אחידה על הקטע [0,10], הסיכוי שייבחר מספר מהקטע [1,2] הוא רק עשירית; הסתברויות רציפות אינן יודעות לספור. עוזי ו. - שיחה 20:35, 12 במרץ 2016 (IST)
- מה שאתם אומרים מעניין. נניח ניסוי מחשבתי שבו ישנה מוכנה המגרילה מספרים פסיידו-אקראיים בין 0 ל10. ומונה הסופר את כמות הפעמים שיצא מספר בין 0 ל10 ומונה שני שסופר את מספר הפעמים שיצא מספר בין 1 ל2. ברור שהמונה הראשון יציג תמיד מספר גדול יותר מהמונה השני, כי הקבוצה השניה היא תת קבוצה בראשונה. האם זה לא מוכיח שיש יותר מספרים בין 0 ל10 מאשר בין 1 ל2?
איך מוצאים מאמר לפי ציטוט?
[עריכת קוד מקור]יש ציטוט:
Fortier A. et al. (2013). Astron. Astrophys., 549, A44.
איך אני מוצא את המאמר הזה? שיטות עם שלבים יתקבלו בברכה. 132.66.137.207 15:34, 16 במרץ 2016 (IST)
- ראשית - להבין מה אתה מחזיק; הקוד שהצגת הוא לא ציטוט (מן המאמר) אלא הפניה (אליו).
- זהה את כתב העת. Astron Astrophys הוא קיצור של Astronomy & Astrophysics.
- מצא את אתר המערכת.
- מצא את המאמר באתר: כאן.
(אפשר לחפש אותו גם במאגרי מידע כלליים; למשל בספריה של המחלקה לאסטרונומיה הקרובה למקום מגוריך). עוזי ו. - שיחה 16:08, 16 במרץ 2016 (IST)
- איך עברת משלב 2 ל3? אני נכנס לאתר של aanda וכותב "Fortier A. et al. (2013)" בשורת החיפוש. הוא לא מוצא לי את המאמר. 132.66.137.207 16:18, 16 במרץ 2016 (IST)
- CTRL-F עושה פלאים במקרים כאלה. תן לאתר קצת פחות מידע (למשל - רק Fortier), והוא ישמח לעזור. עוזי ו. - שיחה 17:54, 16 במרץ 2016 (IST)
- אפשר גם לחפש דרך מאגרי ספרייה באוניברסיטה / טכניון / ספרייה עם גישה למאגרי מידע שיכולים לחפש במגוון ירחונים (Engineering village, scopus ועוד) והם יקשרו אותך לאתר הכתב עת או מקורות המכילים את המאמר. בברכה אמא של גולן - שיחה 22:33, 26 במרץ 2016 (IDT)
- וחיפוש בgoogle scholar הביא אותי מיד למאמר אבל בשביל עותק מלא צריך דרך מחשב של ספרייה אוניברסיטאית אם אתה לא רוצה לקנת בברכה אמא של גולן - שיחה 22:36, 26 במרץ 2016 (IDT)
- אפשר גם לחפש דרך מאגרי ספרייה באוניברסיטה / טכניון / ספרייה עם גישה למאגרי מידע שיכולים לחפש במגוון ירחונים (Engineering village, scopus ועוד) והם יקשרו אותך לאתר הכתב עת או מקורות המכילים את המאמר. בברכה אמא של גולן - שיחה 22:33, 26 במרץ 2016 (IDT)
- CTRL-F עושה פלאים במקרים כאלה. תן לאתר קצת פחות מידע (למשל - רק Fortier), והוא ישמח לעזור. עוזי ו. - שיחה 17:54, 16 במרץ 2016 (IST)
- איך עברת משלב 2 ל3? אני נכנס לאתר של aanda וכותב "Fortier A. et al. (2013)" בשורת החיפוש. הוא לא מוצא לי את המאמר. 132.66.137.207 16:18, 16 במרץ 2016 (IST)
האם יהיה רגע שבו כל כוכבי הלכת יהיו בקו ישר
[עריכת קוד מקור]זאת לא שאלה בפיזיקה, אלא בהיגיון+מתמטיקה.
נניח 8 כוכבי לכת הסובבים את השמש במישור (דו מימד) במעגלים. כל כוכב לכת מבצע סיבוב שלם תוך פרק זמן מוגדר ואין תלות מתמטית מחיבת בין זמני הסיבוב.
נניח שהמערכת מתחילה את הסיבוב כהשמיקום ההתחלתי כוכבי הלכת לאורך מעגל הסיבוב שלהם הוא אקראי. האם במהלך אינסוף זמן נגיע למצב שכל כוכבי הלכת נמצאים בישר אחד? 77.126.164.5 17:39, 26 במרץ 2016 (IDT)
- אני מפרש את "אין תלות מתמטית מחייבת" בהנחה שמשכי הסיבוב בלתי תלויים לינארית מעל הרציונליים. ה*מרכזים* של כוכבי הלכת אמנם לא יתייצבו על ישר אחד, אבל מכיוון שכוכבי הלכת אינם נקודתיים, התשובה חיובית. התורה הארגודית יודעת גם לחשב כמה אירועים כאלה צפויים להתרחש בפרק זמן נתון (וארוך מאד). אבל ראה גם יציבותה של מערכת השמש. עוזי ו. - שיחה 20:45, 26 במרץ 2016 (IDT)
קושי בהוכחה - אליפסה, גיאומטריה אנליטית
[עריכת קוד מקור]d1 ו-d2 הם בהתאמה קטרים באליפסה המאונכים זה לזה. הוכח:
ניסית לחשב את המרחקים של הנקודות שנמצאות על היקף האליפסה ממרכזה ולהשוותן לחצאי הקטרים הנתונים, ולבנות משוואת נוספת באמצעות משפט פיתגורס (שהרי נתון שהם מאונכים), אבל זה יוצא מאוד מפלצתי. מעבר לזה, קיים משפט שאומר שמכפלת השיפועים של מיתר באליפסה ושל הקוטר החוצה אותו הוא . חשבתי שאפשר להשתמש בזה בשאלה הזו, מאחר שקוטר הוא למעשה סוג של מיתר, אך התשובה יוצאת סתמית לחלוטין ולא הגיונית - מאחר ששיפועים אלה מאונכים זה לזה, על המכפלה הנ"ל להיות מינוס 1, ואז יוצא ש-a צריך להיות שווה ל-b. אשמח פתרון. תודה.
- שאלה יפה, שצריך להיות לה פתרון אלגנטי. נסמן נקודות על שני הקטרים ב-(x1,y1) ו-(x2,y2). העובדה שהקטרים מאונכים אומרת ש- ולכן . הצב את השוויון הזה ואת בהפרש , ותקבל אפס. עוזי ו. - שיחה 16:44, 29 במרץ 2016 (IDT)
שלום,
האם העדר פתרון אנליטי לבעיית שלושת הגופים, נובע מהרגישות של הבעיה לתנאי התחלה? האם קיימות בעיות שרגישות באופן דומה לתנאי התחלה, ויש להן פיתרון אנליטי? תודה, 31.154.175.235 20:45, 2 באפריל 2016 (IDT)
- רגישות לתנאי ההתחלה לא אמורה להפריע (בפני עצמה) לפתרון אנליטי. הנה דוגמא פשוטה. נניח ש-a הוא מספר. חשוב על הפונקציה , כלומר החלק השברי של המספר at (כאשר t הוא פרמטר הזמן). שגיאה קלה ב- תיצור בחלוף הזמן שגיאה הולכת וגדלה ב-x. אפשר להמציא דוגמאות שבהן השגיאה גדלה מהר יותר (אקספוננציאלית, למשל). עוזי ו. - שיחה 23:52, 2 באפריל 2016 (IDT)
- למה אתה חושב שיש לבעיה רגישות לתנאי התחלה? הניסיון האנושי של אלפי שנים בכוכב לכת שהוא חלק ממערכת בעלת אפילו יותר משלושה גופים מראה ההפך. eman • שיחה • ♥ 01:40, 3 באפריל 2016 (IDT)
- בעיית שלושת הגופים ידועה כבעיה לא יציבה במובן של רגישות לתנאי ההתחלה. ראה למשל [2]. הפתרונות שאנחנו צופים בהם במערכת השמש (שמחזיקים מעמד כמה מליארדי שנים, ולא רק כמה אלפים) הם פתרונות קרובים למחזוריים; אפילו זה לא הופך אותם ליציבים. עוזי ו. - שיחה 02:50, 3 באפריל 2016 (IDT)
- תודה! 212.179.21.194 08:57, 3 באפריל 2016 (IDT)
- וגם אני השכלתי! תודה! eman • שיחה • ♥ 15:41, 3 באפריל 2016 (IDT)
חידות פיזיקה
[עריכת קוד מקור]במסגרת פעולתי לחיזוקו של פורטל:פיזיקה הוספתי לו חידות אחדות. אבקש שמישהו שמבין יותר ממני בנושא יבדוק את התשובות שנתתי. גם חידות נוספות יתקבלו בברכה. דוד שי - שיחה 07:18, 3 באפריל 2016 (IDT)
- זה חידות שאתה חיברת? או שהן לקוחות מאיפה שהוא? יאצקין52 - שיחה 10:50, 3 באפריל 2016 (IDT)
- בחירה מוצלחת, למעט החידה על הזבוב המטייל בין שתי מכוניות נוסעות, שהיא חידה מתמטית ולא פיזיקלית (אלא אם נוסיף חסם עליון על התאוצה של הזבוב...) עוזי ו. - שיחה 21:47, 3 באפריל 2016 (IDT)
- אלה חידות שמצאתי בכל מיני מקורות, ורק אופן הצגתן הוא שלי.
- החידה על הזבוב היא חידה מתמטית על נושא פיזיקלי, שהרי היא מבוססת על נוסחה פיזיקלית s = vt. נראה לי שיש מקום לחידה שמציגה, על קצה המזלג, את חשיבותה של המתמטיקה בפתרון בעיות בפיזיקה. דוד שי - שיחה 04:27, 4 באפריל 2016 (IDT)
- תודה דוד יאצקין52 - שיחה 15:52, 4 באפריל 2016 (IDT)
החידה על ארכימדס ונקודת המשען מניחה שארכימדס וכדוה"א הם כמו חפצים במאזניים בשדה כבידה קבוע. זה לא נכון, וצריך לפחות להוסיף הערה בחידה. ―אנונימי לא חתם
- הוספתי. דוד שי - שיחה 06:08, 5 באפריל 2016 (IDT)
מבחן סטטיסטי במערך ניסויי
[עריכת קוד מקור]שלום, במערך ניסויי אם יש לי 3 משתנים (אחד תלוי ושניים בלתי תלויים) כמותיים, באיזה מבחן סטטיסטי עלי להשתמש? במבחן שונות דו כיווני? תודה רבה מראש:)132.70.66.14 14:13, 4 באפריל 2016 (IDT)
- זו שאלה כללית מדי. מה אופי המשתנים? עוזי ו. - שיחה 18:25, 4 באפריל 2016 (IDT)
- משתנה אחד מסולם שמי, משתנה מסולם קטגוריאלי ומשתנה מסולם רווח.
- ניתוח שונות דו-כיווני אמור להתאים. עוזי ו. - שיחה 19:28, 6 באפריל 2016 (IDT)
- תודה רבה!! ואם משתנה אחד שמי ושניים מסולם רווח אז אצטרך להשתמש בניתוח שונות חד כיווני מסוג MANCOVA (כשמשתנה אחד מתופעל, אם זה משנה למשהו)?
- ניתוח שונות דו-כיווני אמור להתאים. עוזי ו. - שיחה 19:28, 6 באפריל 2016 (IDT)
- משתנה אחד מסולם שמי, משתנה מסולם קטגוריאלי ומשתנה מסולם רווח.
"באיזו תרכובת יש הכי הרבה יסודות?"
[עריכת קוד מקור]זו השאלה ששאלה אותי בתי. אולי נכון יותר לנסח באיזו מולקולה מוכרת ונפוצה יחסית מעורבים הכי הרבה יסודות שונים? אני מנחש שמדובר בחלבון כלשהו או באיזו תרכובת אנאורגנית מיוחדת.
- אין תשובה אחת לשאלה הזו, זה תלוי מה בדיוק מחפשת בתך. חלבונים מורכבים ממספר קטן של יסודות שונים: פחמן, חמצן, חנקן, מימן, וגופרית. בחלבונים בודדים יש גם סלניום. החלבון הגדול ביותר בגוף האדם הוא טיטין. אני משער שלא קשה מאוד להכין פולימר ארוך עם קבוצות צד מגוונות שתעשינה כלציה לכל יסוד שתרצה. ―אנונימי לא חתם
- כתוצאה מהשאלה יצאנו למסע ולמדנו די הרבה. למדנו שחלבונים הם מולקולות ענקיות, אבל מספר היסודות שבהם לא גדול. מאידך, בכימיה אי-אורגנית מצאנו את פצלת השדה שהמולקולה הבסיסית שלה מכילה עשרה יסודות.
הפיכת חומר לרדיואקטיבי/מינן?
[עריכת קוד מקור]איך נקרא המדד שמודד את היכולת של חומר להפוך לרדיואקטיבי? איזה חומרים יותר פגיעים איזה פחות? האם קרינה מיננת היא קרינה רדיואקטיבית? אם לא אותה שאלה לגבי קרינה מייננת. נאמר לי למשל שאדם שעובד עם מכשייר רנטגן שוטף אחר כך את הבגדים שלו. לא ידעתי שהבגדים עלולים להיות מסוכנים כי נחשפו לקרינה הזאת. תודה.
- קרא את הערכים קרינה רדיואקטיבית וקרינה מייננת. קרינה רדיואקטיבית על סוגיה השונים היא מייננת, כיוון שמדובר באנרגיות גבוהות. לא כל קרינה מייננת היא רדיואקטיבית. קרינת רנטגן, ואולטרה סגול מייננות, ומקורן עשוי להיות לא גרעיני. אינני יודע מה הסיבה לנקיון הבגדים, אך אם ישנה, אנחש שהיא כימית. חומר עשוי להפוך לרדיואקטיבי אם הוא נחשף לקרינה רדיואקטיבית שחדרה ושינתה את מבנה הגרעין (להערכתי רנטגן לא מספיק). לקרינת ניוטרונים כושר חדירה גבוה, אך לא כל האיזוטופים שיווצרו יהיו רדיואקטיבים. ―אנונימי לא חתם
- כל דברי האלמוני נכונים. אני אוסיף שלדעתי רוב החומרים הרדיואקטיביים לא הפכו להיות רדיואקטיביים, אלא היו כאלה (מאז היווסדות מערכת השמש), והם חלק משרשרות של חומר רדיואקטיבי אחד, שהופך לאחר וכו' וכו'. חומר יכול להפוך להיות רדיואקטיבי אם פגעה בו קרינה (ככה למשל נוצר רוב הפחמן-14) אבל לדעתי זה מיעוט של המקרים.
- לגבי שטיפת הבגדים, יכול להיות ניחוש אחד של האלמוני, שנאי מניח שהוא התכוון שהקרינה המייננת יננה את המולוקולות של החומר, וגרמה בו לשינויים כימיים שחלקם יכול להיות מסוכן. אלב אולי גם באמת הקרינה שינתה מבנים של גרעינים, והפכה אותם לרדיואקטיביים. אני באמת לא יודע מה מהניחושים, אם בכלל, נכון. eman • שיחה • ♥ 02:34, 13 באפריל 2016 (IDT)
התנהגות של פונקציה סתומה
[עריכת קוד מקור]נקבע מספר . נתבונן לכל d טבעי במספר שמקיים . אנחנו טוענים שההתנהגות של N כתלות בd היא בקירוב לינארית, כלומר שהגדלה של d ב־1 תגדיל את N בערך באותה כמות בלי תלות בd. איך אפשר להראות שקצב הגדילה הוא אכן לינארי? אפשר לראות את ההתנהגות הזאת בתמונה המצורפת, שבה הצבעים השונים מתאימים לערכי d שונים. בתמונה רואים טענה חזקה יותר, שהקווים הם בקירוב מקבילים – כלומר עבור ערכי p שונים מדובר באותו קבוע. למה התופעה הזאת מתרחשת? --אדי פ' - שיחה 20:55, 23 באפריל 2016 (IDT)

- ותר על ההנחה ש-d טבעי. נסמן . המשתנים N,d קשורים באילוץ f(N,d)=0, ואפשר לחשב את הנגזרת של אחד מהם לפי השני: . כפי שאתה רואה, הנגזרת הזו לא תלויה ב-p. עוזי ו. - שיחה 22:29, 23 באפריל 2016 (IDT)
- תודה. כלומר כללית על קווי גובה של פונקציה במספר משתנים השינוי במשתנה אחד כתלות באחר לא תלוי בקו הגובה המסוים. [נדמה לי שהנגזרת היא ]--אדי פ' - שיחה 23:11, 23 באפריל 2016 (IDT)
בעיות NP-קשות
[עריכת קוד מקור]אהלן,
אני מכיר את ההגדרה הקלאסית של שפה (בעיית הכרעה) -קשה.
1. מהי ההגדרה לבעיית קירוב NP-קשה?
2. אם אומרים על בעית הבטחה A שהיא NP-קשה, האם הכוונה היא שלכל קיימת רדוקציה פולינומית כך ש:
, ?
תודה
- בעיית k-קירוב (בד"כ מניחים ש-k קבוע, אבל במקרים מתקדמים במיוחד דנים גם ב-k-ים לא קבועים) היא NP-קשה אם בעיית ההכרעה האם יש k-קירוב (=האם יש פתרון שערכו לפחות 1 חלקיי k מהערך של הבעיה האופטימלית, ביחס לפונקציית הערכה נתונה כלשהי) היא NP-קשה.
- כן. 213.8.204.72 08:02, 1 במאי 2016 (IDT)
- לא הבנתי את 1. אם לבעיה מסוימת יש פתרון אופטימלי כלשהו, אז ברור שישנו פתרון s המקיים (למשל, הפתרון האופטימלי עצמו), ואני מניח שהרעיון הוא שהבעיה קשה אם קשה למצוא קירוב כזה. עדין לא ברור לי איך זה מוגדר במדויק, ואיך הופכים את זה לבעיית הכרעה.
- מישהו בכל זאת??
- קודם כל, אם יש פתרון אופטימלי, ברור שיש פתרון מקורב. אבל אם אין פתרון אופטימלי, עדיין עשוי להיות פיתרון מקורב.
- שנית, בעיית ההכרעה היא השאלה: האם קיים פתרון המהווה k-קירוב לבעיה?
- לדוגמה, 2-קירוב ל-SAT זה האם קיימת השמה שמספקת לפחות מחצית מהנוסחאות ב-SAT? (כפי שבטח למדת בשיעור, הבעיה הזאת ספציפית היא ב-P).
- עכשיו זה ברור? אם לא - מה לא ברור? 2001:BF8:200:FF99:20C3:1C1A:FA44:F962 12:35, 9 במאי 2016 (IDT)
- למיטב הבנתי תמיד יש פתרון אופטימלי. אם למשל אנחנו מעונינים במציאת עץ פורש מינימלי, קליקה מקסימלית בגרף וכו', אז יתכן שיהיה קשה למצוא פתרון כזה (או אפילו קשה למצוא לו קירוב), אך תמיד קיים עץ פורש שהוא מינימלי, קליקה שהיא מקסימלית וכו'. ואם קיימים כאלה, אז ודאי שקיימים עץ פורש שמשקלו לכל היותר פי 3 מגודל העץ המינימלי (למשל, העץ הפורש המינימלי), קליקה שגודלה לפחות חצי מגודל הקליקה המקורית (למשל, הקליקה המקסימלית עצמה), אז עדין לא ברור לי איך יתכן שהבעייה שקולה לבעיית ההכרעה האם קיים K-קירוב. (כי הקירוב תמיד קיים).
- לגבי הדוגמא על ה-SAT: אני מניח כוונתך היא ל-3-CNF-SAT, ולנוסחה כזו תמיד יש השמה שמספקת לפחות 7/8 מהפסוקיות, אז בפרט יש השמה שמספקת לפחות חצי, ככה שהתשובה לבעיית ההכרעה הנ"ל היא תמיד כן. (2-CNF-SAT, כלומר, נוסחה בה בכל פסוקית יש שני ליטרלים, היא ב-P).
- אשמח לשמוע מה אני מפספס כאן.
- רוב תודות!
- כשאומרים "פתרון אופטימלי" לא מתכוונים לפתרון הכי טוב שקיים בבעיה הנוכחית. אלא מתכוונים לפתרון שהוא "מושלם". למשל, ב-SAT הכוונה היא לפתרון שמספק את כל הפסוקיות. ולכן, פתרון זה לא תמיד קיים. ולכן, פתרון k-קירוב הוא קירוב ביחס לפתרון המושלם, ולא ביחס לפתרון הכי טוב שאפשר בבעיה הנוכחית. ולכן, גם הוא לא תמיד קיים. למשל, בשאלת הקליקה שואלים: האם יש קליקה בגודל לפחות m בגרף, אז הפתרון האופטימלי זה קליקה בגודל m ופתרון של 2-קירוב (לעומת הדוגמה עם הקירוב ל- SAT, הקירוב הזה הוא כן NP-complete) זה קליקה בגודל לפחות m/2. כך, בעיית 2-קירוב במקרה זה: האם יש קליקה בגודל לפחות m/2 בגרף.
- הערה: זאת הגרסה כבעיית הכרעה לקליקה מקסימלית. הגרסה של בעיית החיפוש (סביר שבכיתה למדתם את 2 הגרסאות) עבור בעיית קליקה מקסימלית היא: תמצא את הקליקה המקסימלית בגרף. ובעיית 2-קירוב זה: תמצא קליקה המהווה לפחות חצי מהגודל של הקליקה המקסימלית בגרף. כפי שהזכרתי, 2 הבעיות (הרגילה, והקירוב שלה, הן בבעיית החיפוש והן בבעיית ההכרעה) הן NP-complete.
- בגרסה של קליקה כבעיית חיפוש אכן תמיד קיים קליקה מקסימלית, כי לכל גרף יש איזושהי קליקה שהיא המקסימלית עבורו - כי פה האופטימלי זה ביחס לגרף, וגם הקירוב זה גם ביחס אליו, ולכן גם הוא תמיד קיים, אבל היות והשאלה פה הייתה בעיית חיפוש ולא להכריע אם זה קיים, לכן זה עדיין הגיוני.
- אגב, עץ פורש מינימלי זה ב-P.
- לגבי הדוגמה על 2-קירוב ל-SAT, לזה התכוונתי כשאמרתי שזה ב-P: התכוונתי שתמיד קיים במקרה זה 2-קירוב מהמשפט מהכיתה (למרות שבמחשבה שנייה, זה לא היה חכם להביא משהו שתמיד קיים בו 2-קירוב כשהשאלה שלך הייתה למה זה לא תמיד קיים... לכן, הבאתי הפעם עוד דוגמאות).
- עכשיו זה ברור? 07:54, 10 במאי 2016 (IDT)
- כמעט....
- אני מבין את כל מה שכתבת, אבל עדין לא רואה כאן תשובה לשאלה שלי, אז כנראה הייתי צריך לנסח אותה באופן ברור יותר.
- ממה שאני מכיר, המינוח בעיות אופטימיזציה מתיחס לבעיות של מציאת מינימום/ מקסימום. כלומר, בעיות חיפוש (ולא הכרעה) בהן תמיד קיים פתרון, ואנו רק מחפשים את הפתרון האופטימלי. ועל כן, גם המושג של בעיית קירוב (ע"פ מה שהכרתי והתכוונתי), מתיחס למציאת קירוב ביחס לבעיות כנ"ל.
- בכל אופן, מה שהתכוונתי לשאול זה: מתי בעיית קירוב לבעיית חיפוש מוגדרת להיות NP-קשה (או שלמה)? או באופן כללי יותר: מתי בעיית חיפוש מוגדרת להיות NP-קשה?
- אני מבין שהרעיון הוא שבעיית חיפוש היא NP-קשה אם לא נצפה למצוא לה אלגוריתם פולינומי (תחת ההנחה ). ובאופן ספציפי, קירוב K לבעיית חיפוש הוא NP-קשה אם לא קיים אלגוריתם פולינומי המוצא קירוב כנ"ל (שוב, תחת ההנחה ). מה שאני מחפש זו הגדרה פורמלית יותר (כמו ההגדרה עם הרדוקציות עבור בעיות הכרעה NP-קשות).
- בקשר לבעיית הההכרעה שהזכרת, מציאת קליקה בגודל m בגרף, ומציאת קירוב 2, כלומר קליקה בגודל m/2 בגרף זה - קשה לי להאמין שלזה יקרא בעית קירוב. זה פשוט החלפת הקלט לבעיית ההכרעה CLIQUE, בקלט . למעשה זו אותה בעיה, אך עם פרמטר שונה, ורעיון הקירוב לא בא כאן לידי ביטוי.
- בכל מקרה, תודה רבה על התשובה המפורטת! ואשמח מאד לתשובה אחרונה על השאלה ששאלתי כאן.
- הדרך שאני מכיר זה: להפוך את בעיית החיפוש לבעיית הכרעה (למשל, מציאת קליקה מקסימלית = בהינתן גרף וקליקה, האם הקליקה מקסימלית? בעיית קירוב מתאימה: בהינתן גרף וקליקה, האם הקליקה הזאת לפחות בגודל של 1/k מהגודל של הקליקה המקסימלית בגרף? שים לב, שזה שקול לשאלה: בהינתן גרף, ומספר m, האם יש קליקה בגודל לפחות m?). ואז: בעיית חיפוש היא NP-קשה אם בעיית ההכרעה המתאימה לה היא NP-קשה.
- כל זה בהנחה ואנחנו מדברים על רדוקציות מהסוג הרגיל, הנקראות רדוקציות "קארפ". אבל יש סוג נוסף של רדוקציות: רדוקציות טיורינג, ובהן לא חייבים להמיר את בעיית החיפוש לבעיית הכרעה: פשוט תראה שבאמצעות אלגוריתם פולינומי - בהנחה וקיים כזה - שפותר את בעיית החיפוש הנידונה, אתה יכול לפתור בעיית חיפוש אחרת, שידוע שהיא NP-קשה. 213.8.204.65 10:21, 13 במאי 2016 (IDT)
מקדם הולכת חום לSiO2 גז
[עריכת קוד מקור]אני רוצה לדעת מה הConvective Heat Transfer Coefficients בהערכה גסה עבור גז SiO2 טהור בטמפרטורה ולחץ סבירים לגז כזה (נניח 15000 קלווין ו200000000000 דין לסמ"ר). 132.66.137.207 13:21, 29 באפריל 2016 (IDT)
רעיון - אולי טפשי..
[עריכת קוד מקור]יש לי רעיון שהוא אולי טפשי - כיוון שאין לי די ידע בנושא: אם ניתן לתארך את שאריות הקרינה של השמש שבתוך חומר כלשהו (דהיינו לדעת לחלק את הקרינה לפי תאריך הגעתה), (אולי ע"י זה ש"כיום, כשמתאפשרות מדידות הספק מדויקות (שמבוצעות בלוויינים), ידוע שקרינת השמש משתנה ללא הפסקה, אך במידה מעטה - כמה עשיריות אחוז"-מהערך קרינת השמש), ועל בסיס ניתוח דרכי ההגעה וההסטה של קרינה מזויות שונות לתוך החומר הספציפי, ניתן יהיה לשחזר את הכיוונים שמהם הגיעה אותה קרינה וכך לשחזר את ה"תמונה" שהחומר "ראה"? Uhbcrd451 - שיחה 17:44, 3 במאי 2016 (IDT)
- לא טיפשי, אבל טיפה לא ברור. ראשית: על איזה סדר גודל של זמן אתה מדבר? האם לקבוע שניה ספיפית, או תאריך ושעה או, אולי לקבוע את המיליון שנה שבו הקרינה נקלטה? שנית: האם אתה מדבר על חומר טבעי או על גלאי מיוחד שמיוצר לצורך קליטת קרינה? Corvus-TAU - שיחה 20:41, 3 במאי 2016 (IDT)
- באופן ראשוני חשבתי על חומר טבעי (כמובן יתכן שיש חומרים שיותר מתאימים מאחרים) לקבוע משהו בין שניה לתאריך ושעה (כאשר הקונצפט היה להשתמש בחומרים מהעבר כמעין מצלמות-למפרע), אולם כמובן, גם פחות מזה מעניין אותי, תודה רבה Uhbcrd451 - שיחה 22:02, 7 במאי 2016 (IDT)
- אני לא חושב שיש בטבע חומרים רגישים ברמת השניות, וספק ברמת הדקות. חומרים כאלה מיוצרים במיוחד לצורך צילום בדרך כלל. זמן חשיפה מספיק עבור חומרים בטבע שיגרום לשינוי מורגש הוא הרבה יותר ארוך מיממה ולכן לא תצליח לשחזר את התמונה ברמת הזווית. זה כמו לנסות לצלם תהליך שלוקח אלפית שניה עם מצלמה ביתית. בשביל לבצע את הניסוי שאתה מתאר צריך מיכשור שנבנה במיוחד למטרה זו. Corvus-TAU - שיחה 13:15, 9 במאי 2016 (IDT)
- באופן ראשוני חשבתי על חומר טבעי (כמובן יתכן שיש חומרים שיותר מתאימים מאחרים) לקבוע משהו בין שניה לתאריך ושעה (כאשר הקונצפט היה להשתמש בחומרים מהעבר כמעין מצלמות-למפרע), אולם כמובן, גם פחות מזה מעניין אותי, תודה רבה Uhbcrd451 - שיחה 22:02, 7 במאי 2016 (IDT)
מערכת משואות
[עריכת קוד מקור]הי לכולם,
איך פותרים את התרגיל ?
תודה
- זו לא מערכת משוואות, אלא משוואה לא לינארית בנעלם אחד. למשוואה מהסוג הזה בדרך כלל אין פתרון אלמנטרי (ראה (אנ')), אבל במקרה הזה קל לנחש שני פתרונות. על-ידי גזירת ההפרש אפשר להוכיח בקלות שאין יותר משניים. עוזי ו. - שיחה 10:11, 8 במאי 2016 (IDT)
- עוזי ו., זה מבני גורן. אני תלמיד ב-007 ומנסה להשלים חומר לבד אבל בני גורן לא מסביר איך לפתור את המשוואה הזו (אלא רק מסביר שיש שתי דרכים אחת גרפית עליה מסביר וזו שנראת לו ברורה מאליו...). היו שתי פונקציות והשוואתי אותן.מה זה גזירת הפרש? ―אנונימי לא חתם
- פיתרון אנליטי (כלומר ממש חישוב) של משוואה זו מסובך למדי ולא ברמת בגרות. מה שאתה יכול לעשות זה פיתרון גרפי: כלומר לצייר שתי פונקציות ו על אותו הגרף ולחפש את נקודת החיתוך שלהם. בשביל לצייר את הפונקציה אתה צריך לקחת מספר נקודות (קח כמה Xים פשוטים כמו וכדומה בשביל לעשות סקיצה. Corvus-TAU - שיחה 13:26, 8 במאי 2016 (IDT)
- עוזי ו., זה מבני גורן. אני תלמיד ב-007 ומנסה להשלים חומר לבד אבל בני גורן לא מסביר איך לפתור את המשוואה הזו (אלא רק מסביר שיש שתי דרכים אחת גרפית עליה מסביר וזו שנראת לו ברורה מאליו...). היו שתי פונקציות והשוואתי אותן.מה זה גזירת הפרש? ―אנונימי לא חתם
- הפתרון שרואים מיד הוא x=0 כי את זה קל להציב. עבור x=1 גם יש פתרון. השיטה הקלה היא גם לצייר כל צד ולחפש נקודות חיתוך אמא של גולן - שיחה 20:07, 8 במאי 2016 (IDT)
- התבונן (בכל זאת) בהפרש בין שתי הפונקציות, כלומר . הנגזרת היא , והיא שווה לאפס רק בנקודה אחת: . בין כל שני שורשים של פונקציה (גזירה), הנגזרת מוכרחה להתאפס לפחות פעם אחת (זה משפט רול), ומכאן שלפונקציה שלנו לא יכולים להיות יותר משני שורשים, שאותם מצאת באמצעות ניחוש (ישיר או מונחה-גרפים). עוזי ו. - שיחה 21:23, 8 במאי 2016 (IDT)
תודה רבה לכולם. לא הבנתי איך ממש עושים את המשוואות האלו. הבנתי שאפשר בעיניים לראות (השאלה אם מותר בבגרות) או בגרף ונראה לי שפשוט אלך על גרף ואתעלם כרגע מהשאלות האלו. תודה רבה לכולן על התמיכה.
- כפי שכתבתי לעיל, אין למשוואה כזו פתרון אלמנטרי (היינו, אין שיטה לפתור אותן, מלבד ניחוש מושכל). עוזי ו. - שיחה 10:06, 9 במאי 2016 (IDT)
- אין כמו מראה עיניים - תראה למה הכוונה בפתרון גרפי. גם אם לא מצאת את נקודות החיתוך בניחוש, אתה יכול לשער לפי ההצבות.

בברכה אמא של גולן - שיחה 10:39, 9 במאי 2016 (IDT)
כיצד יהיה ניתן לראות מחר את מעבר כוכב חמה על פני השמש?
[עריכת קוד מקור]לפני קצת יותר משנה היה ליקוי חמה, קניתי בכמה שקלים משקפיים מתאימים וצפיתי בו. כמובן - אין מדובר בציוד אופטי יקר ומתוחכם, אלא במשקפי קרטון.
מחר צפוי "ליקוי חמה" במובן זה שכוכב חמה יעבור על פני השמש, ואני משער שמה שניתן יהיה לראות בעזרת ציוד מתאים זו נקודה קטנה שתחלוף על פניה.
האם "הציוד" מאשתקד אמור לאפשר לי לראות את זה? גרי רשף - שיחה 10:55, 8 במאי 2016 (IDT)
- עקרונית כן. אבל אני לא אהיה מופתע אם הנקודה תהיה קטנה מדי בשביל לראות את הטרנזיט. Corvus-TAU - שיחה 13:28, 8 במאי 2016 (IDT)
- גרי שלום, הנקודה תהיה קטנה מדי מכדי לראות רק במשקפיים. צריך משקפות או טלסקופ לפחות, ואפשר לעשות זאת בהקרנה הפוכה. כאן פרטים על המעבר ועל שידור באינטרנט. בברכה אמא של גולן - שיחה 16:11, 8 במאי 2016 (IDT)
- תודה רבה! גרי רשף - שיחה 16:21, 8 במאי 2016 (IDT)
- גרי, Corvus-TAU פתחתי את מעבר כוכב חמה על פני השמש. כיוון שאני ברכבת, אתם מוזמנים לערוך. בברכה אמא של גולן - שיחה 19:23, 8 במאי 2016 (IDT)
- ב"הקרנה הפוכה" עם משקפת שהיא מספיק טובה בשביל לראות כתמי שמש, יהיה אפשר לראות את זה? כי ממה שראיתי פה [3] זה גם קטן יחסית לכתמי השמש. eman • שיחה • ♥ 19:28, 8 במאי 2016 (IDT)
- אנסה מחר לעשות ניסוי הקרנה הפוכה עם הילדים. הטענה באינטרנט שזה אפשרי עם משקפת. אם אתה באיזור חיפה אתה מוזמן להצטרף. אמא של גולן - שיחה 20:00, 8 במאי 2016 (IDT)
- תודה, אלב אני מחר נע בין ב"ש לשדרות, ויש לי משקפת. תוהה רק האם להביא את המשקפת איתי (:
- eman • שיחה • ♥ 22:14, 8 במאי 2016 (IDT)
- אנסה מחר לעשות ניסוי הקרנה הפוכה עם הילדים. הטענה באינטרנט שזה אפשרי עם משקפת. אם אתה באיזור חיפה אתה מוזמן להצטרף. אמא של גולן - שיחה 20:00, 8 במאי 2016 (IDT)
- תודה רבה! גרי רשף - שיחה 16:21, 8 במאי 2016 (IDT)
- גרי שלום, הנקודה תהיה קטנה מדי מכדי לראות רק במשקפיים. צריך משקפות או טלסקופ לפחות, ואפשר לעשות זאת בהקרנה הפוכה. כאן פרטים על המעבר ועל שידור באינטרנט. בברכה אמא של גולן - שיחה 16:11, 8 במאי 2016 (IDT)
ורק בשביל שחו"ח אף אחד שצופה בדיון במקרה לא יבין באופן מוטעה - אסור בשום אופן להסתכל ישירות על השמש, ובוודאי שלא דרך משקפת או טלסקופ (אלא אם כן זה טלסקופ מיוחד לצורך זה). כן אפשר להקרין עם משקפת תמונה על מסך שנמצא מאחוריה. eman • שיחה • ♥ 19:31, 8 במאי 2016 (IDT)
שאלה על משוואה עם מטריצה בינארית
[עריכת קוד מקור]היי, יש לי 3 טענות שאני לא יודע אם הן נכונות, ולא הצלחתי לא להוכיח אותן ולא למצוא להן דוגמה נגדית (אני מאמין שהראשונה מביניהן לא נכונה, והשתיים האחרות כן נכונות).
תהי A מטריצה בינארית בגודל , שסכום כל שורה ועמודה שלה הוא 3. נסמן (כלומר, וקטור עמודה שמורכב רק מ-1-ים).
- האם נכון שלמשוואה , יש פתרון מעל אםם יש לה פתרון מעל (כתת קבוצה של , לא כ-)?
- בהנחה והטענה הקודמת לא נכונה - האם נכון ש- , כלומר שקיים אינדקס i כך שלכל פתרון מעל שאינו מעל מתקיים כי ? (אם הטענה הקודמת נכונה, אז זאת נכונה באופן ריק).
- בהנחה והטענה הקודמת לא נכונה האם נכון כי ?
אם הטענות האלה לא נכונות - אשמח מאוד לדוגמה נגדית :)
תודה רבה רבה מראש! :) 213.8.204.65 09:33, 14 במאי 2016 (IDT)
אמת או שקר: מים מלוחים רותחים בטמפ' גבוהה יותר
[עריכת קוד מקור]אני זוכר משיעורי כימיה בטכניון, שאנחנו מוסיפים מים בזמן בישול לא בשביל הטעם, אלא בשביל להעלות את טמפרטורת הרתיחה של המים.
מצד שני קראתי לא מזמן שמדובר במיתוס שכן הכמות המלח הדרושה להעלות את טמפרטורת המים במעלה אחת היא גובהה מאוד ומים מלוחים כל כך לא נצרכים על ידי האדם. אז האם זו אמת או מיתוס? 31.168.14.82 09:07, 16 במאי 2016 (IDT)
- בשורה הראשונה התכוונת לאמר "שאנחנו מוסיפים 'מלח...". בכל אופן זה כנראה מיתוס. לפי הערך "העלאת נקודת הרתיחה" (אנ') אין לכך השפעה מעשית: "at the approximate concentration of salt in water for cooking (10 g of salt per 1 kg of water, or 1 teaspoon per quart), the ebullioscopic increase is approximately 0.17 °C (0.31 °F), which will arguably make no practical difference for cooking, although salt may add to flavors." שנילי - שיחה 13:06, 16 במאי 2016 (IDT)
- אני למדתי בשיעור כימיה (אוניברסיטאי) הפוך - מלח גורם לכך שהמים ירתחו דווקא בטמפרטורה נמוכה יותר, ולפיכך מהר יותר במהלך הבישול.
- זה ממש לא נכון. שנילי - שיחה 13:11, 18 במאי 2016 (IDT)
- אני למדתי בשיעור כימיה (אוניברסיטאי) הפוך - מלח גורם לכך שהמים ירתחו דווקא בטמפרטורה נמוכה יותר, ולפיכך מהר יותר במהלך הבישול.
כמה ישרלים יש מעל גובה מסויים?
[עריכת קוד מקור]גבהים של אנשים מתפלגים באופן נורמלי סביב ערך תוחלת כלשהו, נכון? אם כך על ידי פונקציית שגיאה ניתן להעריך כמה אנשים יש מעל או מתחת לגבוה מסוים? אז כמה נשים מתחת לגובה 1.65 מתגוררות היום בישראל? 93.172.170.217 12:36, 20 במאי 2016 (IDT)
- גובה הוא אחת הדוגמאות הקלאסיות להתפלגות נורמלית, אם כי להתפלגות האמיתית יש גבנוניות חיובית (כלומר, זנבות שמנים יותר מאלו שחוזה ההתפלגות הנורמלית). הגובה הממוצע של נשים בישראל הוא 1.66 מטר [4], ולכן התשובה לשאלתך היא - קרוב למחציתן. לתשובה מדוייקת יותר צריך לדעת מהי סטיית התקן. עוזי ו. - שיחה 13:01, 20 במאי 2016 (IDT)
משושה המורכב ממשולשים
[עריכת קוד מקור]איך קוראים למשושה המורכב ממשולשים? זאב קטן - שיחה 19:50, 1 ביוני 2016 (IDT)
- למה כוונתך? כל משושה אפשר להרכיב ממשולשים. עוזי ו. - שיחה 20:45, 1 ביוני 2016 (IDT)
- נגיד זה.
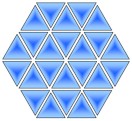
|

|
| Order 2 | Order 2 with numbers 1–24 |
בערך באנגלית קוראים לזה T-hexagons, השאלה היא איך קוראים לזה בעברית. זאב קטן - שיחה 20:52, 1 ביוני 2016 (IDT)
- קראתי את הערך באנגלית (אנ') וכמה ערכים סמוכים, ואי אפשר לסמוך עליהם בעניינים טרמינולוגיים. זה שמישהו אי-שם קרא למבנה מסויים בשם, לא אומר שיש צורך בשם מיוחד, או שזה השם שנמצא בשימוש (אם בכלל). אפשר לקרוא לזה "משושה משולש" (היינו משושה ששילשו אותו). עוזי ו. - שיחה 22:23, 1 ביוני 2016 (IDT)
- אם כך אקרא לזה משושה משולוש. תודה רבה. זאב קטן - שיחה 22:46, 1 ביוני 2016 (IDT)
- קראתי את הערך באנגלית (אנ') וכמה ערכים סמוכים, ואי אפשר לסמוך עליהם בעניינים טרמינולוגיים. זה שמישהו אי-שם קרא למבנה מסויים בשם, לא אומר שיש צורך בשם מיוחד, או שזה השם שנמצא בשימוש (אם בכלל). אפשר לקרוא לזה "משושה משולש" (היינו משושה ששילשו אותו). עוזי ו. - שיחה 22:23, 1 ביוני 2016 (IDT)
פולינומי לורן אינם חוג מנה של פולינומים
[עריכת קוד מקור]איך רואים שהחוג אינו איזומורפי לאף מנה של החוג ?--אדי פ' - שיחה 21:30, 8 ביוני 2016 (IDT)
- המנה היחידה שממדה אינסופי היא החוג עצמו, ושם האברים ההפיכים הם הסקלרים בלבד. עוזי ו. - שיחה 22:35, 8 ביוני 2016 (IDT)
- הטיעון מעיד שאין איזומורפיזם של ־אלגברות ביניהם. למה הוא מראה גם שאין איזומורפיזם של חוגים ביניהם? (הלא איזומורפיזם חוגים לא חייב לשמור על הממד כאלגברה.)--אדי פ' - שיחה 22:50, 8 ביוני 2016 (IDT)
- אכן. אם כך, אפשר להשוות את החוג לתת-החוג הנוצר על-ידי האברים ההפיכים. עוזי ו. - שיחה 23:19, 8 ביוני 2016 (IDT)
- הטיעון מעיד שאין איזומורפיזם של ־אלגברות ביניהם. למה הוא מראה גם שאין איזומורפיזם של חוגים ביניהם? (הלא איזומורפיזם חוגים לא חייב לשמור על הממד כאלגברה.)--אדי פ' - שיחה 22:50, 8 ביוני 2016 (IDT)
היקום הנצפה
[עריכת קוד מקור]ניסיתי לחפש בערכים אבל לא מצאתי תשובה תמציתית. לכאורה, בלתי אפשרי לדעת על מיליארדי גלקסיות, אם הן מרוחקות מיליוני שנות אור ואף יותר. את השמש אנו רואים באיחור של 8 דקות. אז את קצה שביל החלב אנו רואים באיחור של עשרות אלפי שנות אור. המסקנה שלי: את אלה המרוחקים מאוד איננו רואים אלא יודעים עליהם. איך? Mr. W ~ T ~ בית המשפטים העליון 21:14, 9 ביוני 2016 (IDT)
- אם הנחת המפץ הגדול נכונה, אזי בזמן התרחקות הגלקסיות נותר אחריהן שובל האור שלהן, ולכן תיאורטית אנחנו אמורים להיות יכולים לראות את כולם. ביקורת - שיחה 21:29, 9 ביוני 2016 (IDT)
- בעיה אחרת היא, שלא הכל עומד בזווית "נכונה" למבט שלנו מכדור הארץ, ועלינו להסיק קיומם של גופים לפי תאוריות כבידה, לאור גופים אחרים באזור שכן ידועים לנו, הם ומסלולם. ביקורת - שיחה 21:31, 9 ביוני 2016 (IDT)
- אז אדם שמפקפק בתיאוריית המפץ יפקפק על כורחו במידות היקום? שאלה נוספת איך יודעים שהיקום הנצפה או רק חלק מזערי מהיקום כולו (כפי שמופיע בערך)? Mr. W ~ T ~ בית המשפטים העליון 21:37, 9 ביוני 2016 (IDT)
- מי שלא מכיר בתיאוריה יצטרך לחפש הסברים אחרים להתפשטות הנצפית של היקום (הנצפה) ולכך שלא מתחוללות התנגשויות קטסטרופליות בגבולות השטח המתפשט. מידות היקום לא מוסכמות וכמדומני שגם לא משוערות, הן נעלם. למעשה אי אפשר תיאורטית להניח גבול פיזי של היקום. אבל אני חושב שמקובל לראות בקרינת הרקע הקוסמית את גבולו המשוער של שטח ההתפשטות.
- לגבי שאלתך השנייה, אין לי איך לנסח את זה במילים טובות יותר מאלו שמצאתי בוויקיפדיה: "לפי המודל הקוסמולוגי הרווח כיום, קצב התפשטותו הנוכחי של היקום הוא אקספוננציאלי, בעוד שאופק האירועים גדל לינארית בזמן. כתוצאה מכך, ככל שעובר יותר זמן, כך פחות ופחות חלקים מהיקום נגישים עבורנו ולעולם לא יהיה לנו קשר פיזיקלי (ובפרט, קשר סיבתי) איתם. משיקולי אינסופיות היקום (ובאופן אנלוגי לטיעון בפסקה הראשונה של סעיף זה) נובע שיש אינסוף "בועות" כמו שלנו, המופרדות לחלוטין זו מזו.". סוף ציטוט.
- אני הדיוט בתחום, מקווה שיבוא גם המומחה, זו רק עזרה ראשונה. ביקורת - שיחה 21:51, 9 ביוני 2016 (IDT)
- אז אדם שמפקפק בתיאוריית המפץ יפקפק על כורחו במידות היקום? שאלה נוספת איך יודעים שהיקום הנצפה או רק חלק מזערי מהיקום כולו (כפי שמופיע בערך)? Mr. W ~ T ~ בית המשפטים העליון 21:37, 9 ביוני 2016 (IDT)
- בעיה אחרת היא, שלא הכל עומד בזווית "נכונה" למבט שלנו מכדור הארץ, ועלינו להסיק קיומם של גופים לפי תאוריות כבידה, לאור גופים אחרים באזור שכן ידועים לנו, הם ומסלולם. ביקורת - שיחה 21:31, 9 ביוני 2016 (IDT)
- אני לא קוסמולוג, אתרום מעט. אחד הדברים המפתיעים בשמי הלילה זה החושך שלהם. אם מניחים בשלילה שהיקום הוא אינוספי בגודלו וגם קיים אינסוף זמן, אז היינו מקבלים אור מכל נקודה על השמיים. ובכל זאת, השמיים שחורים נקודות. ראה הפרדוקס של אולברס.
- קצב התפשטות היקום היה גבהה ממהירות האור בתקופת האינפלציה. ואכן, אזורים מרוחקים ביותר שאנו צופים בהם ה"עבר" רחוק ואזורים עוד יותר מרוחקים אפילו לא נצפים. Corvus,(Nevermore) 22:10, 9 ביוני 2016 (IDT)
- ביקורת דיברתי על היקום הנצפה. הוא לא נעלם ויש לו מידות מדויקות בערך האנגלי.
- Corvus, אני מתקשה לעקוב אחר כל המושגים שאתה מדבר עליהם, אם כי אני מבין קצת לאן אתה חותר. תכל'ס איך יודעים את מידות היקום (הכוונה לא שאני מתכוון ללמוד עכשיו איך מודדים זאת, אלא באופן כללי באלו אמצעים. ברור שלא בצפייה (הרי אי אפשר לצפות למרחקים שהם גדולים בהרבה שנות אור מגיל היקום, וגם אם כן לאחר מיליארדי שנים אולי הכל השתנה כבר). אז במה? בחישובים פיזיקליים? מתמטיים? חייזריים? Mr. W ~ T ~ בית המשפטים העליון 23:17, 9 ביוני 2016 (IDT)
- אם קראתי נכון שאלת על היחס בין מידות היקום הנצפה למידות היקום בכלל, "איך יודעים שהיקום הנצפה הוא רק חלק מזערי מהיקום כולו". לא כן? ביקורת - שיחה 23:20, 9 ביוני 2016 (IDT)
- אה. וגם לדעתי הערך היקום הנצפה לא כתוב טוב, והוא גם מילוני. למחיקה מהירה. ביקורת - שיחה 23:21, 9 ביוני 2016 (IDT)
- כתבתי לפני התנגשות עריכה: כן זה גם. כי איך אפשר בכלל לשער או להעריך או לדעת שיש בכלל יקום שלא נצפה אם הוא לא נצפה (הרי גם הנצפה הוא לא נצפה). 2 שאלותיי הן אותה שאלה בעצם. איך יודעים משהו שהוא לכאורה בלתי נצפה, בלתי מורגש, בלתי מדיד = בלתי ניתן לידיעה?
- הוספתי לאחר התנגשות עריכה: כן. לכן פניתי גם לערך האנגלי כפי שהזכרתי. Mr. W ~ T ~ בית המשפטים העליון 23:25, 9 ביוני 2016 (IDT)
- המממ... לא יודע איך להגיד את זה בצורה תקינה פוליטית
 . אבל אין לנו מושג מה גדול היקום כולו. החלטה שהיקום הנצפה הוא חלק קטן מהיקום נובעת רק משיקולים לוגיים. בין השיקולים יש את כוח הכבידה. אם היקום הנצפה היה "בערך הכל", אז הוא היה הולך ומתכווץ תחת כבידה של עצמו (כל דבר מושך כל דבר אחר עד שהכל מרכז במרכז). אבל אם הוא מוקף בהרבה חומר, אז החומר מסביב מושך אותו ומונע כיווץ. ואם עכשיו קוסמולוג יקרא את מה שכתבתי, הוא כנראה ירצה להרוג אותי.
. אבל אין לנו מושג מה גדול היקום כולו. החלטה שהיקום הנצפה הוא חלק קטן מהיקום נובעת רק משיקולים לוגיים. בין השיקולים יש את כוח הכבידה. אם היקום הנצפה היה "בערך הכל", אז הוא היה הולך ומתכווץ תחת כבידה של עצמו (כל דבר מושך כל דבר אחר עד שהכל מרכז במרכז). אבל אם הוא מוקף בהרבה חומר, אז החומר מסביב מושך אותו ומונע כיווץ. ואם עכשיו קוסמולוג יקרא את מה שכתבתי, הוא כנראה ירצה להרוג אותי. - גדול היקום הנצפה דווקא כן בא מתצפיות ישירות בטלסקופים, עם התחשבות בכך שהיקום הולך ומתפשט. Corvus,(Nevermore) 00:10, 10 ביוני 2016 (IDT)
- Corvus, אז תצפית באמצעות טלסקופ מקרבת את העין באלפי שנות אור? זה לא נשמע הגיוני. Mr. W ~ T ~ בית המשפטים העליון 06:39, 14 ביוני 2016 (IDT)
- לא. היא עוזרת למקד אור שכבר עשה את הדרך, אבל הוא מפוזר מכדי לראותו בעין בלתי מזויינת. ביקורת - שיחה 09:35, 14 ביוני 2016 (IDT)
- ממקד וגם מגביר. הטלסקופים של החלל הרחוק הם לא רק מערכת מראות/עדשות. הם מכשירים אופטיים האוספים מידע שבלתי נראה בעין בלתי מזוינת או עם טלסקופ רגיל. לדגומה גלקסיות חשוכות מדי או קרינה בצבעים שאנו לא יכולים לצפות בהם (קרינה אינפה-אדומה, אולטרה-סגולה וכדומה). Corvus,(Nevermore) 10:01, 14 ביוני 2016 (IDT)
- בסדר, אבל אם הם לא מאפשרים "לקרב" מרחק של אלפי שנות אור לעין, בהכרח שהמידות של היקום הנצפה לא התקבלו על סמך תצפיות ישירות. האם נכון להגיד "מידות היקום הנצפה הן תוצאה של תצפיות למרחקים קרובים + חישובים פיזיקליים (הכבידה) ומתמטיים"? Mr. W ~ T ~ בית המשפטים העליון 13:12, 14 ביוני 2016 (IDT)
- כשאתה צופה בשמש אתה רואה את העבר הלא רחוק (כ-8 דקות ממך). כשאתה מסתכל על כוכבים רחוקים, אתה רואה עבר יותר רחוק (מאות עד אלפי שנים). בטלסקופ פשוט אתה יכול לראות כוכבים שלא נראים בעין בלתי מזוינת כפי שהם היום לפני עשרות ומאות אלפי שנים. הטלסקופ לא באמת "מקרב". הוא רק נותן לך אפשרות טכנית לראות אובייקטים שהעין שלך לא מסוגלת לראות (שאלות רזולוציה סף עוצמה מינימלית). טלסקופים משוכללים מודרניים יודעים לזהות אור מאובייקטים מרוחקים מאוד-מאוד של מיליירדי שנות אור. משמעות הדבר הוא כמובן שהאור שנקלט בגלאים של הטלסקופ מגיע מגלקסיות שהיו קיימות לפני מיליירדי שנים. עכשיו לשאלת החישוב: אנחנו יודיעם מסיבות אלו ואחרות שהמרחב עצמו משתנה. כלומר בהערכת מרחקים (שזו שאלה מאוד רצינית. מדידת מרחקים רחוקים בהתבסס על מרחקים קרובים יודעים זה נושא בפני עצמו) יש לקחת בחשבון את מהירות ההתרחקות עקב התפשטות היקום. כך שגדול הייקום הנצפה הוא הערכה הלוקחת בחשבון את זה שהמרחב מתפשט. Corvus-TAU - שיחה 15:32, 14 ביוני 2016 (IDT)
- הסבר מצוין. אז למשל, הנתונים בתבנית שב-M59 המרוחקת 60 מיליון שנות אור הם נתונים המשקפים את מצב הגלקסיה לפני כ-60 מיליון שנה? או נתונים של הגלקסיה כיום שהתקבלו מתוך צפייה + חישובים המתחשבים בהתפשטות החומר וחישובים פיזיקליים ומתמטיים אחרים? Mr. W ~ T ~ בית המשפטים העליון 14:22, 15 ביוני 2016 (IDT)
- Mr. W, אתה בהחלט רואה את "העבר" ככל שאתה מסתכל יותר רחוק. יכול להיות שקורה עכשיו משהו מדהים בגלקסיית אנדרומדה, אבל נגלה את זה רק בעוד 2.5 מיליון שנה. הייקום עצמו הרבה יותר גדול מהיקום הנצפה. כאן יש הסבר טוב למה היקום הנצפה הוא רק חלק קטן מהיקום כולו. בברכה אמא של גולן - שיחה 14:33, 15 ביוני 2016 (IDT)
- וואו. לא חשבתי על זה ככה. אני אנסה לבדוק מול חוקרים. אתה מבין שהערכת זמנים והערכת מרחקים זה פחות או יותר אותו הדבר. באמת שאלה מעניינת. Corvus-TAU - שיחה 14:35, 15 ביוני 2016 (IDT)
- אם אני מבין נכון, בדיוק בשל העובדה שהערכת זמן/מרחק בתחום הזה זהה, המידע מתייחס למה שאנחנו רואים, כלומר לעבר של הגלקסיה ולא למצבה עכשיו. אין טעם לנסות לנבא דבר כזה, כשאין לנו שמץ של מושג על המשתנים הרבים. ביקורת - שיחה 18:26, 15 ביוני 2016 (IDT)
- זה נראלי מגוחך ומצחיק שרוב רובה של הקוסמולוגיה מתארת היסטוריה כ"כ רחוקה. אולי נקטלג את קטגוריה:קוסמולוגיה ואת כל דפיה בקטגוריה:היסטוריה של היקום
 ?
? - מצד שני, אפשר להסתכל ע"ז כתיאור המצב ב"הווה" שלנו, למרות שזה ה"עבר" שלהם. הרי הזמן הוא יחסי. Mr. W ~ T ~ בית המשפטים העליון 18:32, 15 ביוני 2016 (IDT)
- בהגדרה, זו האמת לאמתה. את זמן ליקוי החמה אנחנו לא מקטלגים לפי שעון השמש. ביקורת - שיחה 18:45, 15 ביוני 2016 (IDT)
- ועוד דבר, אם היה נחצה מחסום מהירות האור, היה מתבטל מחסום הזמן, יכלת להשיג סרטון של (כמעט) כל אירוע שהתרחש בעבר על כדור הארץ תחת כיפת השמים. ביקורת - שיחה 18:48, 15 ביוני 2016 (IDT)
- תודה ביקורת.
- Corvus-TAU ואמא של גולן, עכשיו רק שמתי לב שיש בעיה בדבריכם. כי אם לא ניתן להעריך או לצפות רק למרחקים נצפים בהתחשב במהירות האור, הרי שגודל היקום הנצפה מכדור הארץ ועד לקצהו בכל כיוון היה צריך להיות כמעט אותו מספר שנות אור כגיל היקום (כלומר, כ-14 מיליארד שנים, ובהתאמה כ-14 מיליארד שנות אור). אבל לפי הערך האנגלי המרחק מאיתנו לקצה היקום הנצפה הוא הרבה יותר גדול: כ-46 מיליארדי שנות אור.
- הנה ציטוט משם: "The comoving distance from Earth to the edge of the observable universe is about 14.26 gigaparsecs (46.5 billion light years or 4.40×1026 meters) in any direction". Mr. W ~ T ~ בית המשפטים העליון 19:33, 15 ביוני 2016 (IDT)
- האם לא השמטת שוב מהחישוב את התפשטות היקום? ביקורת - שיחה 19:38, 15 ביוני 2016 (IDT)
- אה נכון. "comoving distance" (אנ'). באמת הגיע הזמן לכתוב את הערך הבסיסי הזה כאן במקום את המצביעים הערבים נעים בכמויות אדירות לקלפי ונאום הקומץ. Mr. W ~ T ~ בית המשפטים העליון 20:48, 15 ביוני 2016 (IDT)
- האם לא השמטת שוב מהחישוב את התפשטות היקום? ביקורת - שיחה 19:38, 15 ביוני 2016 (IDT)
- ועוד דבר, אם היה נחצה מחסום מהירות האור, היה מתבטל מחסום הזמן, יכלת להשיג סרטון של (כמעט) כל אירוע שהתרחש בעבר על כדור הארץ תחת כיפת השמים. ביקורת - שיחה 18:48, 15 ביוני 2016 (IDT)
- בהגדרה, זו האמת לאמתה. את זמן ליקוי החמה אנחנו לא מקטלגים לפי שעון השמש. ביקורת - שיחה 18:45, 15 ביוני 2016 (IDT)
- זה נראלי מגוחך ומצחיק שרוב רובה של הקוסמולוגיה מתארת היסטוריה כ"כ רחוקה. אולי נקטלג את קטגוריה:קוסמולוגיה ואת כל דפיה בקטגוריה:היסטוריה של היקום
- אם אני מבין נכון, בדיוק בשל העובדה שהערכת זמן/מרחק בתחום הזה זהה, המידע מתייחס למה שאנחנו רואים, כלומר לעבר של הגלקסיה ולא למצבה עכשיו. אין טעם לנסות לנבא דבר כזה, כשאין לנו שמץ של מושג על המשתנים הרבים. ביקורת - שיחה 18:26, 15 ביוני 2016 (IDT)
- בסדר, אבל אם הם לא מאפשרים "לקרב" מרחק של אלפי שנות אור לעין, בהכרח שהמידות של היקום הנצפה לא התקבלו על סמך תצפיות ישירות. האם נכון להגיד "מידות היקום הנצפה הן תוצאה של תצפיות למרחקים קרובים + חישובים פיזיקליים (הכבידה) ומתמטיים"? Mr. W ~ T ~ בית המשפטים העליון 13:12, 14 ביוני 2016 (IDT)
- ממקד וגם מגביר. הטלסקופים של החלל הרחוק הם לא רק מערכת מראות/עדשות. הם מכשירים אופטיים האוספים מידע שבלתי נראה בעין בלתי מזוינת או עם טלסקופ רגיל. לדגומה גלקסיות חשוכות מדי או קרינה בצבעים שאנו לא יכולים לצפות בהם (קרינה אינפה-אדומה, אולטרה-סגולה וכדומה). Corvus,(Nevermore) 10:01, 14 ביוני 2016 (IDT)
- לא. היא עוזרת למקד אור שכבר עשה את הדרך, אבל הוא מפוזר מכדי לראותו בעין בלתי מזויינת. ביקורת - שיחה 09:35, 14 ביוני 2016 (IDT)
- Corvus, אז תצפית באמצעות טלסקופ מקרבת את העין באלפי שנות אור? זה לא נשמע הגיוני. Mr. W ~ T ~ בית המשפטים העליון 06:39, 14 ביוני 2016 (IDT)
- המממ... לא יודע איך להגיד את זה בצורה תקינה פוליטית
- אה. וגם לדעתי הערך היקום הנצפה לא כתוב טוב, והוא גם מילוני. למחיקה מהירה. ביקורת - שיחה 23:21, 9 ביוני 2016 (IDT)
- אם קראתי נכון שאלת על היחס בין מידות היקום הנצפה למידות היקום בכלל, "איך יודעים שהיקום הנצפה הוא רק חלק מזערי מהיקום כולו". לא כן? ביקורת - שיחה 23:20, 9 ביוני 2016 (IDT)
- משתמש:Mr. W, היום קיבלתי תשובה, באנגלית. החוקר אליו פניתי הוא מאיר שמעון (Meir Shimon).
- ציטוט|Hi, Please excuse the overdue response, I was bogged down with other urgent work. As to your question, "The galaxy M59 is 60Mly way from us" means that "it was in that distance 60Myr ago". Recall that an "event" in relativity (either special relativity or general relativity) is (t,x,y,z); You cannot separate space from time, and a consistent description of events must be 4-dimensional. The answer to your question can be best visualized if you plot a spacetime diagram (only the t and x coordinates for simplicity) in which "here and now" are at the origin of this spacetime coordinate system. Then draw the past light cone whose apex is at the origin. All the light you receive "here and now" must travel along this light cone. The event of light emission from M59 must then be located at negative t ("now" is defined as t=0) and at x different from zero. So, this means that you observe M59 as it was at t=-60 million years back and at a distance 60Mly from here. You must specify both space and time coordinates, as I just did, in order to fully and unabiguously describe what you actually observe.
- מקווה שזה מבהיר לך. Corvus-TAU - שיחה 10:20, 21 ביוני 2016 (IDT)
- מבהיר היטב. מסתבר שצדקתי. מדהים לחשוב על כך. כל מה שאנחנו יודעים על היקום מוקפא בזמן! אנו יודעים על היקום אפס מוחלט ככל שזה נוגע לזמננו אנו! ייתכן שה-M59 הוא כיום בכלל כדור ארץ מלבלב, והחוצנים שעליו בטוחים שהם יודעים על כדור הארץ הכל, אבל מה שהם כותבים בוויקיפדיה החוצנית על כדורנו החביב זה גונדוונה ואיך הדינוזאורים נכחדו נעבעך...
- המון תודות Corvus-TAU, Mr. W ~ T ~ בית המשפטים העליון 15:07, 21 ביוני 2016 (IDT)
הגיל בו בפעם הראשונה: איזה התפלגות זו?
[עריכת קוד מקור]נניח אני רוצה לעשות סקר "מתי פעם ראשונה..." (נניח רכבת על אופניים, התנשקת, אכלת חומוס). עושה הסיטגרמה של כמות אנשים כפונקציה של גיל. איזו סוג התפלגות זה יצא? האם נורמלי? נניח הסקר ענק עד אינסופי.
וגם אני שואל את השאלה "מתי התחלת לעבוד" (כלומר החל מאותו הרגע אתה כבר עובד כל הזמן)- זה אותה השאלה כמו קודם, נכון? 31.168.14.82 09:48, 10 ביוני 2016 (IDT)
- זה לא עונה לשאלה, אבל: 1. אין סיבה לצפות להתפלגות נורמלית (שהיתה עשויה להופיע רק אם אותה פעם ראשונה מתרחשת כתוצאה מאירועים מצטברים ובלתי תלויים המתרחשים *בטור*). 2. גודל הסקר אינו רלוונטי להתפלגות. עוזי ו. - שיחה 15:39, 10 ביוני 2016 (IDT)
- אבל איזו התפלגות זו תהיה? נגדיר מאורע "הגיל בו בפעם הראשונה טעמת גלידה בטעם תפוז". האנשים לא מכירים אחד את השני ואין סיבה לחשוב שהיה משהו מיוחד שגרם לאכילת גלידת תפוז. אני לא יודע לצפות בכלל איך יראה גרף כזה. די ברור שלי שתהיה דעיכה לגיל המבוגר (מעט אנשים יטעמו זאת לראשונה בגיל 40, עוד פחות בגיל 50 וכמעט אף אחד בגיל 75) אולי אפשר להניח כל מיני הנחות לצרוך הקלה. 93.172.170.217 15:54, 10 ביוני 2016 (IDT)
- אולי התפלגות גמא? זו ההתפלגות שמסכמת כמה שעונים אקספוננציאליים (עם אותה תוחלת). אני נוטה יותר למודל שבו המאורע מתרחש אחרי שמתפרקים (למשל) שבעה הראשונים מתוך עשרה חלקיקים רדיואקטיביים; זה סכום של משתנים אקספוננציאליים, אבל עם תוחלות שונות. עוזי ו. - שיחה 17:11, 10 ביוני 2016 (IDT)
- אבל איזו התפלגות זו תהיה? נגדיר מאורע "הגיל בו בפעם הראשונה טעמת גלידה בטעם תפוז". האנשים לא מכירים אחד את השני ואין סיבה לחשוב שהיה משהו מיוחד שגרם לאכילת גלידת תפוז. אני לא יודע לצפות בכלל איך יראה גרף כזה. די ברור שלי שתהיה דעיכה לגיל המבוגר (מעט אנשים יטעמו זאת לראשונה בגיל 40, עוד פחות בגיל 50 וכמעט אף אחד בגיל 75) אולי אפשר להניח כל מיני הנחות לצרוך הקלה. 93.172.170.217 15:54, 10 ביוני 2016 (IDT)
תרגום המונח overlay network מתחום תקשורת המחשבים.
[עריכת קוד מקור]היוש. בימים האחרונים אני פועל לשיפוץ הערכים בתחום התקשורת האנונימית ברשת. כרגע אני מנסה לתקן את הערך דארקנט. כרגע, חסר בו התיאור של רשת תור, הרשת האנונימית המשפיעה ביותר והרשת אליה מתייחסים לרוב בתקשורת כ"הרשת האפלה" (אין צורך לציין שזה לא מדויק). כרגע אני לא מצליח למצוא תרגום מוצלח למונח overlay network. אני מניח שאין למונח זה תרגום קונצנזואלי, אבל לא למדתי בצורה רשמית את הנושא. אני חושב לתרגם ל"רשת כיסוי" או "רשת תכסית" אבל אני לא בטוח שזה מספיק מובן. אשמח לדעות נוספות. אוּדוֹני - שיחה 01:36, 15 ביוני 2016 (IDT)
מכפלה סקלרית ומכפלה וקטורית
[עריכת קוד מקור]שאלה קצת קשה לניסוח, מקווה שאצליח להסביר את עצמי. באופן פשטני, הייתי אומר שבין מכפלה סקלרית ווקטורית (במרחב התלת מימדי) יש שני הבדלים: 1.המכפלה הסקלרית סופרת את "החלק המקביל" בין שני וקטורים, והמכפלה הוקטורית את "החלק המאונך ביניהם". 2.(מן הסתם) המכפלה הסקלרית היא סקלר והוקטורית היא וקטור.
עקרונית, אין שום בעייה גם להגדיר "מכפלה סקלרית" שסופרת את החלק המאונך, ו"מכפלה וקטורית" שסופרת את החלק המקביל. אבל מסתבר כנראה שלמכפלה כזאת לא יהיה הרבה שימוש. לעומת זאת, למכפלה הסקלרית והוקטורית יש שימושים רבים בפיזיקה. השאלה שלי היא למה זה ככה. איך יצא שברוב המקרים (חישוב מומנט, שדה מגנטי, וכו') המכפלה המאונכת היא וקטור, והמכפלה הסקלרית (חישוב היטל, שימוש בחוק גאוס, וכו') היא סקלר? תודה מראש בלנק - שיחה 16:38, 18 ביוני 2016 (IDT)
- נתחיל מטעות אחת במה שכתבת, שאולי קצת עוזרת לחשוב על תשובה.
- כתבת ש"אין בעיה" להגדיר "מכפלה וקטורית" שסופרת את החלק המקביל. זה לא נכון. כי המכפלה הוקטורית צריכה לתת וקטור שניצב לשני הוקטורים. כאשר שני הוקטורים מקבילים המכפלה הוקטורית האמיתית היא אפס. כי אז אין חלק ניצב. אבל אם היינו מנסים להגדיר מה שהצעת תהיה בעיה. מה יהיה כיוון התוצאה? הרי כששניהם מקבילים יש אינסוף כיוונים ניצבים! eman • שיחה • ♥ 19:36, 18 ביוני 2016 (IDT)
- תודה עימנואל. אני יכול לדמיין כל מיני דרכים לדלג על המכשול הזה, אבל בכל מקרה לא נראה לי שזה עונה לי על השאלה. בלנק - שיחה 20:44, 18 ביוני 2016 (IDT)
- אהבתי את השאלה. לדעתי זו שאלה יפה מאוד, ומעולם לא חשבתי עליה (לבושתי!). אני רק יכול להעיר משהו שאולי יתן כיוון: במקרים שעולים לי כרגע בראש, הכיוון של וקטור המכפלה הוקטורית הוא בעל משמעות מתמטית ולא פיסיקלית. כלומר, זו דרך מתמטית לבצע פעולות אלגבריות באופן שיעשה סדר ויהיה עקבי, אבל אין לו משמעות פשוטה של כיוון במימד שלישי כפי שאנו רגילים לתפוס אותו "במציאות". לדוגמא, כאשר אנו מדברים על מומנט כוח, אנו מכפילים וקטורית את המרחק מציר הסיבוב ואת הכוח. במקרה זה, ברור שהרכיב הרלוונטי הוא הרכיב המאונך, כי רק הוא יוצר סיבוב. מאידך, הגדרת כיוון וקטור המכפלה בסך הכל עוזרת לנו להבדיל בין סיבוב "עם כיוון השעון" או "נגד כיוון השעון", אבל אין מומנט כוח באמת במימד המאונך לשני הוקטורים הנ"ל. ואם נחזור לשאלה שלך: כאשר אנו מדברים על השפעה במימד אחד, שאז המכפלה הרלוונטית היא סקלרית, במקרים שעולים לי לראש מה שרלוונטי זה החלק ה"משותף" של הווקטורים. כאשר אנו מדברים על השפעה דו מימדית, (או, בהכללה, על הרכיב במימד הנוסף), מה שרלוונטי זה החלק שבו הוקטורים "לא שותפים". הבעיה היא שבמקרה כזה ישנם שני כיוונים אפשריים בשני מימדים, וכדי להבדיל ביניהם צריך להגדיר כיוון במימד שלישי. אולי מה שאמרתי זו נקודת התחלה. משה פרידמן - שיחה 11:09, 19 ביוני 2016 (IDT)
- דווקא יש משמעות פיזיקלית. הגדלים שנובעים ממכפלה וקטורית של וקטורים אמיתיים הם מה שנקרא "פסאודו-וקטורים". (מכפלה וקטורית שלהם בעוד וקטור תיתן בחזרה וקטור). המשמעות שכיוונם הוא הרבה פעמים כיוון של ציר. ציר סיבוב (במקרה של מהירות זוויתית, ובמידה מסויימת של מומנט כוח ותנע זוויתי). במקרה לש שדה מגנטי זה ציר שסבובו מטען יסתובב. ובכיוון של ציר יש שרירותיות, ובגלל זה משתמשים בחוק יד ימין בשביל להחליט איזה סיבוב יתאים לאיזה אחד משני כיוונים אפשרים על הציר.
- בכל מקרה, הדברים ה"אמיתיים" קורים במישור שניצב לציר הזה. יש משהו במישור (סיבוב במישור, זרמים וכוחות במישור, ולפעמים אפילו שטח במישור שגם אותו אפשר לתאר בעזרת וקטור שניצב למישור). וכמו שעוזי כתב, בגלל שיש לנו שלושה כיוונים, הכיוון שניצב למישור, מגדיר (עד כדי אחת משתי אפשרויות שנבחרת בצורה שרירותית) את הכיוון של המישור. eman • שיחה • ♥ 15:47, 19 ביוני 2016 (IDT)
- ציר סיבוב איננו נחשב בעיני לבעל משמעות פיסיקלית. זו דרך נוחה לארגן את המחשבה. לא מן הנמנע שאפשר יהיה לתאר תנועה מעגלית ללא ציר סיבוב, בפרו כאשר לא בהכרח מדובר כאן על תנועות מעגליות, או על תנועות בכלל. אין במציאות "ציר סיבוב". משה פרידמן - שיחה 10:49, 20 ביוני 2016 (IDT)
- זה לא ענה על השאלה, אבל זה לא בלתי קשור אליה. ראה את מה שכתבתי למעל בתגובה למשה. אם ניקח את המקרה של מומנט כוח, ברור אינטואיטיבית למה צריך שהכוח והזרוע לא יהיו מקבילים. כי אז לא קורה כלום (הכוח לא יגרום לסיבובב לא ימינה ולא שמאלה). וגם יש משמעות לכיוון של התוצאה. היא (עם קצת זהירות, כי לפעמים יש הפתעות אנטי אינטואיטיביות) קשורה לציר שמסביבו הגוף יסתובב. eman • שיחה • ♥ 15:53, 19 ביוני 2016 (IDT)
- אהבתי את השאלה. לדעתי זו שאלה יפה מאוד, ומעולם לא חשבתי עליה (לבושתי!). אני רק יכול להעיר משהו שאולי יתן כיוון: במקרים שעולים לי כרגע בראש, הכיוון של וקטור המכפלה הוקטורית הוא בעל משמעות מתמטית ולא פיסיקלית. כלומר, זו דרך מתמטית לבצע פעולות אלגבריות באופן שיעשה סדר ויהיה עקבי, אבל אין לו משמעות פשוטה של כיוון במימד שלישי כפי שאנו רגילים לתפוס אותו "במציאות". לדוגמא, כאשר אנו מדברים על מומנט כוח, אנו מכפילים וקטורית את המרחק מציר הסיבוב ואת הכוח. במקרה זה, ברור שהרכיב הרלוונטי הוא הרכיב המאונך, כי רק הוא יוצר סיבוב. מאידך, הגדרת כיוון וקטור המכפלה בסך הכל עוזרת לנו להבדיל בין סיבוב "עם כיוון השעון" או "נגד כיוון השעון", אבל אין מומנט כוח באמת במימד המאונך לשני הוקטורים הנ"ל. ואם נחזור לשאלה שלך: כאשר אנו מדברים על השפעה במימד אחד, שאז המכפלה הרלוונטית היא סקלרית, במקרים שעולים לי לראש מה שרלוונטי זה החלק ה"משותף" של הווקטורים. כאשר אנו מדברים על השפעה דו מימדית, (או, בהכללה, על הרכיב במימד הנוסף), מה שרלוונטי זה החלק שבו הוקטורים "לא שותפים". הבעיה היא שבמקרה כזה ישנם שני כיוונים אפשריים בשני מימדים, וכדי להבדיל ביניהם צריך להגדיר כיוון במימד שלישי. אולי מה שאמרתי זו נקודת התחלה. משה פרידמן - שיחה 11:09, 19 ביוני 2016 (IDT)
- תודה עימנואל. אני יכול לדמיין כל מיני דרכים לדלג על המכשול הזה, אבל בכל מקרה לא נראה לי שזה עונה לי על השאלה. בלנק - שיחה 20:44, 18 ביוני 2016 (IDT)
- כל מכפלה מתקבלת על הדעת צריכה להיות הומוגנית באורך הווקטורים, ולכן - כדי להבין אותה - מספיק לדעת מה קורה כשמכפילים וקטורי יחידה. המכפלה הסקלרית מודדת את (קוסינוס) הזווית בין הוקטורים; והמכפלה הוקטורית משלימה אותם לבסיס באופן אורתוגונלי. תחת ההסבר הזה, אני לא רואה שהמכפלה הסקלרית קשורה ל"חלק המקביל" או שהמכפלה הווקטורית קשורה ל"חלק המאונך".
- הערה נוספת. בעוד שהמכפלה הפנימית תמיד מוגדרת, המכפלה הווקטורית קיימת רק הודות לצירוף מקרים מוזר: 1+1 שווה לממד המרחב שלנו פחות 1. עוזי ו. - שיחה 12:58, 19 ביוני 2016 (IDT)
- לא ענית על השאלה. למה לא הגדירו שתוצאת המכפלה עם ה"קוסינוס" תהיה וקטור וזו שמשלימה אותה אורתוגונלית תהיה סקלר? ולמה ההגדרה הזאת מתארת היטב הרבה תופעות פיסקליות, ובשום מקום בטבע לא נצרכנו להגדרה הפוכה? משה פרידמן - שיחה 13:04, 19 ביוני 2016 (IDT)
- למה כשמחברים שני סקלרים מקבלים סקלר, ולא מידת זמן או נפח? קוסינוס הוא סקלר. משלים אורתוגונלי הוא וקטור. עוזי ו. - שיחה 15:25, 19 ביוני 2016 (IDT)
- תודה לשלושתיכם על התשובות. עוזי, לדעתי הטענה "כדי להבין אותה מספיק לדעת מה קורה כשמכפילים וקטור יחידה" אינה נכונה, כי לא ניתן להבין ממנה את האופן שבו מתייחסים לגודל. למשל, במקרה של מכפלה וקטורית, היה אפשר לעשות מכפלה וקטורית שמשלימה לבסיס אורתוגונלי, אבל הגודל שלה הוא כגודל הממוצע של שני הוקטורים. או פשוט מכפלת גדלי הוקטורים. עבור וקטורי יחידה שתי המכפלות האלו היו נותנות אותו דבר כמו המכפלה הוקטורית המוכרת, אבל כאן בדיוק ייחודה של המכפלה הוקטורית- היא משלימה לבסיס על ידי וקטור שגודלו קשור לחלק המאונך בין שני הוקטורים או ל"מידת המאונכות של שני הוקטורים". בלנק - שיחה 20:10, 19 ביוני 2016 (IDT)
- "כל מכפלה מתקבלת על הדעת צריכה להיות הומוגנית באורך הווקטורים". עוזי ו. - שיחה 21:15, 19 ביוני 2016 (IDT)
- נו, והמכפלות שהצגתי (לפחות השנייה) אינן הומוגניות? בלנק - שיחה 22:09, 19 ביוני 2016 (IDT)
- מכפלת הממוצע אינה הומוגנית. זו שבה האורך הוא מכפלת האורכים היא כן הומוגנית, ובה, כפי שכתבתי, "כדי להבין אותה מספיק לדעת מה קורה כשמכפילים וקטורי יחידה". עוזי ו. - שיחה 22:52, 19 ביוני 2016 (IDT)
- איך מספיק? הרי המכפלה הזאת והמכפלה הוקטורית הרגילה מתנהגות אותו הדבר עבור שני וקטורי יחידה מאונכים. בלנק - שיחה 23:03, 19 ביוני 2016 (IDT)
- מכפלת הממוצע אינה הומוגנית. זו שבה האורך הוא מכפלת האורכים היא כן הומוגנית, ובה, כפי שכתבתי, "כדי להבין אותה מספיק לדעת מה קורה כשמכפילים וקטורי יחידה". עוזי ו. - שיחה 22:52, 19 ביוני 2016 (IDT)
- נו, והמכפלות שהצגתי (לפחות השנייה) אינן הומוגניות? בלנק - שיחה 22:09, 19 ביוני 2016 (IDT)
- "כל מכפלה מתקבלת על הדעת צריכה להיות הומוגנית באורך הווקטורים". עוזי ו. - שיחה 21:15, 19 ביוני 2016 (IDT)
- לעוזי: לא הבנתי את עומק דבריך. מדוע אתה מתייחס לקוסינוס כסקלר (אני לא מתכוון לפונקציה עצמה, אלא לשימוש בה בהקשר של המכפלה הסקלרית)? ואיך אפשר לדבר על וקטור שהוא משלים אורתוגונלי לסקלר? אני לא מבין את משמעות המשפט הזה, אשמח אם תוכל לבאר אותו. (שואל בכנות). משה פרידמן - שיחה 10:49, 20 ביוני 2016 (IDT)
- תודה לשלושתיכם על התשובות. עוזי, לדעתי הטענה "כדי להבין אותה מספיק לדעת מה קורה כשמכפילים וקטור יחידה" אינה נכונה, כי לא ניתן להבין ממנה את האופן שבו מתייחסים לגודל. למשל, במקרה של מכפלה וקטורית, היה אפשר לעשות מכפלה וקטורית שמשלימה לבסיס אורתוגונלי, אבל הגודל שלה הוא כגודל הממוצע של שני הוקטורים. או פשוט מכפלת גדלי הוקטורים. עבור וקטורי יחידה שתי המכפלות האלו היו נותנות אותו דבר כמו המכפלה הוקטורית המוכרת, אבל כאן בדיוק ייחודה של המכפלה הוקטורית- היא משלימה לבסיס על ידי וקטור שגודלו קשור לחלק המאונך בין שני הוקטורים או ל"מידת המאונכות של שני הוקטורים". בלנק - שיחה 20:10, 19 ביוני 2016 (IDT)
- למה כשמחברים שני סקלרים מקבלים סקלר, ולא מידת זמן או נפח? קוסינוס הוא סקלר. משלים אורתוגונלי הוא וקטור. עוזי ו. - שיחה 15:25, 19 ביוני 2016 (IDT)
- לא ענית על השאלה. למה לא הגדירו שתוצאת המכפלה עם ה"קוסינוס" תהיה וקטור וזו שמשלימה אותה אורתוגונלית תהיה סקלר? ולמה ההגדרה הזאת מתארת היטב הרבה תופעות פיסקליות, ובשום מקום בטבע לא נצרכנו להגדרה הפוכה? משה פרידמן - שיחה 13:04, 19 ביוני 2016 (IDT)
שאלה על סוג מסוים של משוואות לינאריות :)
[עריכת קוד מקור]ביטוי הוא "מנוון" אם הוא מהצורה , כאשר הם מקדמים שלמים שסכום הערכים המוחלטים שלהם קטן/ שווה 3 (כלומר, ), ו- הם המשתנים. למשל, x+y-z, x, 2x+y הם ביטויים מנוונים, אבל x+0.5x, x+y+2z אינם ביטויים מנוונים.
משוואה היא "מנוונת" אם ניתן לבצע העברת אגפים ולקבל משוואה שאגף שמאל שלה הוא ביטוי מנוון, ואגף ימין זה המספר 0 או 1. למשל, x=y,2x+y=1 אבל לא x=2y+z,3x=2,4x=0.
מערכת משוואות היא "מנוונת" אם כל משוואה שהיא מכילה היא משוואה מנוונת.
מערכת משוואות נקראת "סגורה" אם מתקיים כי: אם כל פתרון בינארי (כלומר, פתרון מעל {0,1}) של מערכת המשוואות מקיים משוואה מהצורה , או (עבור ), אז משוואה זאת מופיעה במערכת המשוואות. למשל, המערכת {2x+y=1} אינה סגורה, אבל {2x+y=1,x=0,y=1} היא כן סגורה.
שאלה: האם נכון שקיים מספר קבוע m כך שלכל מערכת משוואות מנוונת, מתקיים שאם כל תת קבוצה של המשוואות שלה שגודלה לכל היותר m היא סגורה, אז המערכת כולה סגורה? 213.8.204.79 08:11, 19 ביוני 2016 (IDT)
- אני לא יודע; אבל זו שאלה בקומבינטוריקה ולא באלגברה לינארית. עוזי ו. - שיחה 10:01, 19 ביוני 2016 (IDT)
- נשמע לי שאם בשלילה היה קבוע m כזה, אז מערכת המשוואות הייתה סתירה.
- (נכון?)--אדי פ' - שיחה 22:33, 25 ביוני 2016 (IDT)
- לא נראה לי, כי חסרה לך המשוואה וכן כל אוסף המשוואות .
מה רואים ביום ההיפוך במקומות שונים על כדור הארץ?
[עריכת קוד מקור]היום יום ההיפוך הקייצי, והנה שאלה שמטרידה אותי כבר הרבה זמן: מה רואים בכל מקום?
בקוטב הצפוני השמש כנראה אינה שוקעת, והיא נעה סמוך לקו האופק במשך כל היום.
יותר דרומה מהקוטב אך צפונית לחוג הסרטן (ישראל למשל), השמש זורחת בצפון מזרח, שוקעת בצפון מערב, ומתווה קשת דרומית בתנועתה. נכון?
בחוג הסרטן השמש זורחת בדיוק במזרח, שוקעת בדיוק במערב, ועוברת באמצע הרקיע. נכון? אם כן, האם היום שווה באורכו ללילה? לא הגיוני, אבל זה מה שנובע מכך.
על קו המשווה, השמש זורחת בדרום מזרח, שוקעת בדרום מערב, מתווה קשת צפונית, ומטעמי סימטריה - היום שווה ללילה. נכון?
תודה לכל מי שיכול לענות ולנמק! גרי רשף - שיחה 15:06, 21 ביוני 2016 (IDT)
- בחוג הסרטן, השמש מגיעה באמצע היום בדיוק מעל לראש. נראה לי אבל (אני לא בטוח) שהיא זורחת בכל זאת בצפון מזרח ושוקעת בצפון מערב.
- בקו המשווה לדעתי היום תמיד יהיה שווה ללילה, אבל אני לא בטוח איפה הזריחה והשקיעה. eman • שיחה • ♥ 16:16, 21 ביוני 2016 (IDT)
- ראוי לבנות מודל המדגים את תנועת כדור הארץ ביחס לשמש, הזוויות, וכיצד התנועה מתרגמת למישור המבט מנקודות שונות בכדור הארץ(הגבולות לפחות-דוגמא להתנהגות בכל קבוצת קווי רוחב), אם רק הייתי יודע משהו בגרפיקה או תכנות...18:03, 21 ביוני 2016 (IDT)
- חשבתי על זה שוב, וגם בחצי הכדור הצפוני וגם הדרומי (בין חוגי הקטבים) היום השמש זורחת בצפון מזרח, ושוקעת בדרום מערב.
- בחצי הכדור הצפוני, היא ממשיכה דרומה, במסלול ארוך.
- בחצי הכדור הדרומי היא ממשיכה צפונה, ולכן במסלול קצר. _זה בדיוק הפוך למה שקורה אצלנו בחורף, שהיא מתחילה מדרום מזרח, וממשיכה דרומה במסלול קצר).
- eman • שיחה • ♥ 20:14, 21 ביוני 2016 (IDT)











































![{\displaystyle {\frac {\mathbb {C} [x,y]}{(x+iy+1)+(x^{2}+y^{2}-1)}}\cong \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/132003d01d9364568f11c67f00e96b0560b96c44)

![{\displaystyle \mathbb {C} [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7ee3803a8b93634fdfd422434c5952867b767e)

![{\displaystyle {\frac {\mathbb {C} [x,y]}{(p)+(q)}}\cong {\frac {\mathbb {C} [x,y]}{\ker f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf8ed22fd443e7e7b1b13483a4c0ad8d1761f58)





































![{\displaystyle EXP=\bigcup _{k\in \mathbb {N} }TIME[2^{n^{k}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c476321fc92ab2d5d4635cebda2ae5c7814c5f36)




![{\displaystyle \operatorname {E} \left(X^{n}\right)=i^{-n}\,\left[{\frac {d^{n}}{dt^{n}}}\varphi _{X}(t)\right]_{t=0}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/259b21a3cf46a766fcb217634c4acbe2e0dc5a34)











![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)





























![{\displaystyle \mathbb {C} [x,{\frac {1}{x}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c65a80c2b44ccac1f2e8ad1702773487887d5ce)
![{\displaystyle \mathbb {C} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/244ad3bb0a1d2ff11dde84c4edee1171f670fdb0)










