ויקיפדיה:הכה את המומחה/שאלות במדעים מדויקים/ארכיון1

רציפות

הועבר מויקיפדיה:הכה את המומחה

ההגדרה של רציפות היא $\lim _{{\vec {x}}\to {\vec {x_{0}}}}f({\vec {x}})=f({\vec {x_{0}}})$. האם זה שהוכחתי לפונקציה כלשהי שמתקיים: $\lim _{h\to 0}f({\overrightarrow {x_{0}+h}})=f({\vec {x_{0}}})$ מוכיח רציפות? הכוונה בסימון $({\overrightarrow {x_{0}+h}})\equiv (x_{0}+h,y_{0}+h,z_{0}+h,...)$. 79.177.235.161 11:06, 5 באוקטובר 2012 (IST)

לדעתי יש איזושהי מעידה קטנה באופן שבו סומן h (כסקאלאר במקום כוקטור) מתחת לסימן הגבול, וכן באופן שבו הוגדר (בסוף) הסימון הוקטוריאלי. אני מאמין שהתכוונת לנסח כך:

ההגדרה של רציפות היא $\lim _{{\vec {y}}\to {\vec {x}}}f({\vec {y}})=f({\vec {x}})$. האם זה שהוכחתי לפונקציה כלשהי שמתקיים: $\lim _{{\vec {h}}\to {\vec {0}}}f({\overrightarrow {x+h}})=f({\vec {x}})$ מוכיח רציפות? הכוונה בסימון: $({\overrightarrow {x+h}})\equiv (x_{0}+h_{0},x_{1}+h_{1},x_{2}+h_{2},...)$.

בכל אופן, אם לזה התכוונת, אז התשובה לשאלתך היא חיובית.

אגב: כדי להוכיח זאת, צריך קודם כל להציב ${\vec {h}}={\vec {y}}-{\vec {x}}$. ואח"כ צריך להוכיח (באופן לגמרי טריויאלי) שהגבול של $f({\vec {x}}+{\vec {h}})$ (כאשר ${\vec {h}}$ שואף לאפס) הנו הגבול של $f({\overrightarrow {x+h}})$ (כאשר ${\vec {h}}$ שואף לאפס). סמי20 - שיחה 11:36, 5 באוקטובר 2012 (IST)

הפונקציה שלך רציפה רק בכיוון (1,1,...,1); זה לא אומר שהיא רציפה. עוזי ו. - שיחה 16:34, 5 באוקטובר 2012 (IST)

נכון (ובהתאם להערתך הנכונה, החזרתי לגירסתי הקודמת שהועתקה ע"י אביעד מדף הכה את המומחה, וכן שיניתי את הסימון הסקאלארי האחרון לסימון וקטוריאלי). סמי20 - שיחה 16:56, 5 באוקטובר 2012 (IST)

אפס באלקטרוניקה (ובעיקר במחשבים)

הועבר מויקיפדיה:הכה את המומחה

יצא לי לשמוע על כך ממורה שאפס חשמלי צורך יותר מתח מאשר 1 חשמלי (ולכן משתמשים בד"כ בלוגיקה שלילית). עד אז, חשבתי שאפס חשמלי משמעותו שאין זרם חשמלי, אבל מסתבר שזה לא כך, משום שהמחשב צריך להבדיל איכשהו בין 1 ל 0. נגיד במקרה שבו מזרימים מידע בכבל, יהיה אפשר לקבוע מה 1 ומה 0 לפי מרווחי הזמן בין ה 1ים, אבל זה לא מדויק במיוחד, כי כל עיכוב מכל סיבה יגרום להזרמת אפסים, אם לדוגמא הכבל מחבר בין שני מחשבים והתוכנה שאחראית להעביר את המידע דרך הכבל נתקעה מאיזשהי סיבה. בנוסף לזה, מסתבר שחוץ מ 1 ו 0 קיים TriState, שזה בעצם אומר שרכיב חומרה לא מחובר (מזרים 0). לכן, אני רוצה לדעת איך בעצם מתבטא האפס החשמלי ברמה הפיזית. כשחיפשתי על זה מידע בוויקיפדיה האנגלית והעברית לא מצאתי על זה מידע, גם לא בגוגל, והדבר הקרוב ביותר לזה שמצאתי זו שאלה על למה בכלל צריך אפס בחשמל - התשובה עסקה בהזרמת חשמל כמקור אנרגיה ולא במכשירים אלקטרוניים, שצריכים לשנות זרמים, ובמחשב - שזקוקים לו כדי לבטא מידע בתאי זיכרון או הוראות מעבד. (¯`gal´¯)‎ - שיחה 18:09, 5 באוקטובר 2012 (IST)

במערכות שונות יכולים להגדיר את המשמעות של 1 ושל 0 בצורה שונה. בדרך כלל מדובר שתי רמות מתח שונות: מעל לרמת מתח מסוימת תחשב ל־1 ומתחת לרמה מסוימת: 0 (או אולי דווקא להפך). מבחינה עקרונית אין כאן יותר מדי בעיות וחשוב ר שכל הרכיבים במעגל יסכימו על ההגדרה. מבחינה מעשית ברור שיש משמעות לפרטים הקטנים ולכן יכול להיות ש־0 יוגדר כמתח של 0 (לדוגמה: מתחת ל־1V) או אולי דווקא שלילי (מתחת ל־‎-2V). המספרים בדוגמאות מומצאים ולא לקוחים מתקן מציאותי.

TriState, או מצב של עכבה גבוהה, הוא הפיכת הרכיב למעיין נגד (או בצורה מאוד פשטנית: הפיכתו למעין נתק). בדרך זה הוא לא יכפה את מתח הכניסה שלו על המוצא. זה מאפשר לרכיב אחר שמחובר על אותו הקו לבוע את ערכו. כלומר: זה מאפשר לשני רכיבים או יותר לכתוב (לא בו זמנית) לקו נתונים משותף או לקו תקשורת דו־כיווני. Tzafrir - שיחה 01:02, 7 באוקטובר 2012 (IST)

יעקוביאן

הועבר מויקיפדיה:הכה את המומחה

איך אפשר לחשב יעקוביאן של העתקה $T(u,v)=(u+v,2v,u^{2})$ אני נתקע עם דטרמיננטה של מטריצה לא ריבועית... 109.65.224.151 12:03, 6 באוקטובר 2012 (IST)

לא בטוח שלא תתיקע בשלב הבא, אבל תתחיל מלכתוב $T(u,v,w)=(u+v,2v,u^{2})$. eman • שיחה • ♥ 14:09, 6 באוקטובר 2012 (IST)

ואז יעקוביאן חייב לצאת אפס, כי אחת השורות/עמודות בדטרמיננט היא 0 (גוזרים לפי W). 109.65.224.151 14:25, 6 באוקטובר 2012 (IST)

נורמל בכדוריות

הועבר מויקיפדיה:הכה את המומחה

מהו נורמל למעגל היחידה בקואורדינטות כדוריות? 109.65.224.151 13:56, 6 באוקטובר 2012 (IST)

הנורמל לכל נקודה על מעגל היחידה הוא הווקטור המוגדר על ידי הנקודה ומרכז המעגל (ראשית הצירים). • ♀♂ • קלאו • שיחה • 16:44, 6 באוקטובר 2012 (IST)

ברור. אבל למה הוא שווה בכדוריות? 109.65.224.151 16:55, 6 באוקטובר 2012 (IST)

הקורדינטות של הוקטור מראשית הצירים לנקודה שוות לקורדינטות של הנקודה. פתרון תרגיל בית באופן עצמאי מספק יותר ועוזר להפנים בצורה טובה יותר את החומר. • ♀♂ • קלאו • שיחה • 23:02, 6 באוקטובר 2012 (IST)

היקף אליפסה

מה הנוסחה הסופית להיקף אליפסה הנתונה על ידי $(x/a)^{2}+(y/b)^{2}=1$? 79.176.241.165 09:32, 7 באוקטובר 2012 (IST)

לא קיימת נוסחה אלמנטרית. ראה אינטגרל אליפטי. דניאל • תרמו ערך 09:37, 7 באוקטובר 2012 (IST)

צריך להיות "היקף אליפסה". בנצי - שיחה 01:15, 21 באוקטובר 2012 (IST)

האם יש כזה דבר שנקרא טרפז חד זוית או כהה זוית?

הועבר מויקיפדיה:הכה את המומחה

האם יש כזה דבר שנקרא טרפז חד זוית או כהה זוית? 46.210.13.183

בטרפז יש לפחות זווית אחת קהה ואחת חדה. שנילי - שיחה 16:55, 7 באוקטובר 2012 (IST)

אלא אם כן הוא מלבן. בברכה, MathKnight (שיחה) 17:03, 7 באוקטובר 2012 (IST)

לכל מרובע שאינו מלבן יש זווית אחת לפחות שהיא קהה ולפחות אחת שהיא חדה (משום ממוצע הזוויות במרובע הוא 90 מעלות). דניאל • תרמו ערך 17:10, 7 באוקטובר 2012 (IST)

לפי הגדרה מצמצמת לטרפז רק שתי צלעות מקבילות ולכן אינו יכול להיות מלבן או מקבילית. שנילי - שיחה 20:49, 7 באוקטובר 2012 (IST)

זו הגדרה שנויה במחלוקת. משרד החינוך דוגל בהגדרה המצומצמת, למרות שניתן לראות בטרפז הכללה של מקבילית.

לצורך עניין זה, תוכל להגדיר גם קו ישר כטרפז, שפשוט כל הקווים בו חותכים זה את זה לכל אורכם(אז תהיה זווית שהיא גם 180 מעלות וגם אפס) אך לרוב לא נותים להתייחס למקרה שכזה שכן הוא נוגד חלק מהמשפטים הבסיסיים של הגיאומטריה.Exx8 - שיחה 22:04, 7 באוקטובר 2012 (IST)

זו הגדרה נפוצה אך מטופשת. היא מסבכת את הדיון במרובעים שלא לצורך כפי שמסביר הערך היטב. דניאל • תרמו ערך 00:18, 8 באוקטובר 2012 (IST)

מה זה זווית?

הועבר מויקיפדיה:הכה את המומחה

זוית \ זווית - מונח שכולנו שומעים מדי פעם. מהי ההגדרה של מונח זה?. אם מרובע אפשר להגדיר כ "עצם בעל ארבע פינות", אז איך נגדיר זווית? או פינה?.

מרובע מוגדר כארבע נקודות (לעתים בתוספת התנאי שאף שלוש מהן אינן על ישר אחד), כך שאין צורך להגדיר זווית בשבילו. כפי שכתוב בערך זווית, זווית היא מדד המודד את כמות הסיבוב שעושה ישר אחד כדי להתלכד עם ישר אחר. אפשר להגדיר את המדד באמצעות המושג רדיאן שבתורו מוגדר אך ורק על ידי המושג אורך. דניאל • תרמו ערך 17:19, 7 באוקטובר 2012 (IST)

ואפשר לנקוט בגישה אחרת של בניית הגאומטריה באמצעות אלגברה. אז המרחב מוגדר כמרחב מכפלה פנימית (ראה המרחב האוקלידי) שבמסגרתו זווית בין וקטורים a ו-b מוגדרת באופן טכני כ-$\arccos({\frac {a\cdot b}{|a||b|}})$. דניאל • תרמו ערך 17:27, 7 באוקטובר 2012 (IST)

הגדירו מעליי לדעתי בצורה מעולה. יש לי הגדרה אינטואטיבית. אם תסתכל על שני ישרים שנחתכים, ותסמן את נקודת החיתוך כמוקד,

בכל המעגלים שתיצור וללא תנאי מהו גודל רדיוסם, יחסם חלק זהה מההיקף יחסית לההיקף הכולל של המעגל .ליחס הזה אנחנו קוראים זווית.זו אחת הסיבות לדעתי שכל כך פשוט להשתמש ברדיאנים.Exx8 - שיחה 21:46, 7 באוקטובר 2012 (IST)

אינטרגל משטחי סוג שני

כתוב לנו שאינטגרל משטחי סוג שני (שטף דרך משטח) הוא $\iint _{S}(F\cdot {\hat {n}})ds=\iint _{D}F\cdot (R_{u}\times R_{v})dudv$, כאשר R היא פרמטריזציה של המשטח.

השאלה היא האם צריך לנרמל את ה$R_{u}\times R_{v}$ או שהנירמול כבר "כלול" בנוסחה? 109.67.217.60 18:27, 8 באוקטובר 2012 (IST)

שאלה קלה בהסתברות

שאלה מאוד קלה, רק להבין את האינטואיציה. למה אם יש לי a תאים וn חלקיקים אז ישנם $a^{n}$ אפשרויות לסידור? 79.176.209.152 21:15, 8 באוקטובר 2012 (IST)

כל חלקיק צריך לבחור מבין a תאים אפשריים, ולכן המערכת בוחרת מבין $\,\underbrace {a\cdot a\cdot \,\cdots \,\cdot a} =a^{n}$ מצבים. עוזי ו. - שיחה 21:44, 8 באוקטובר 2012 (IST)

כל חלקיק שואל את עצמו "לאיזה תא אני מגיע" ויש לו a אפשרויות, עד כאן ברור. למה כופלים בין אפשרויות של חלקיק ראשון לשני (נגיד n=2)?

איך אותה המערכת תתנהג אם אני אגיד שאסור לשים יותר מחלקיק אחד בכל תא? נניח יש הרבה יותר תאים מחלקיקים. 79.176.209.152 22:01, 8 באוקטובר 2012 (IST)

לכל בחירה של החלקיק הראשון יש a בחירות של החלקיק השני, וצריך לסכם את כל האפשרויות: a+a+a+...+a=a^2. (אבל האמת היא שכופלים משום שההגדרה של כפל היא "עוצמת המכפלה הקרטזית של קבוצות מהעוצמה המתאימה").

כשמוסיפים מגבלות על המערכת, ספור בהדרגה: החלקיק הראשון יכול לבחור איזה מבין a התאים שירצה; השני צריך לבחור מבין a-1, השלישי מבין a-2, וכן הלאה. גם כאן מכפילים. עוזי ו. - שיחה 22:11, 8 באוקטובר 2012 (IST)

כיפה

למה כיפה (גאומטריה) היא דו מימדית ולא תלת מימדית? סול במול - שיחה 15:26, 9 באוקטובר 2012 (IST)

אולי יהיה לך קל יותר להבין את זה אם תחשוב על ישר. אפשר להגדיר ישר במרחב דו מימדי (מישור), מרחב תלת מימדי או במרחב n מימדי, אך הישר עצמו הוא חד מימדי. • ♀♂ • קלאו • שיחה • 15:35, 9 באוקטובר 2012 (IST)

לתיאור נקודה בכדור תלת מימדי דרושות 3 קואורדינטות כדוריות. לתאור נקודה על פני ספירה נדרשות 2 קואורדינטות כי הרדיוס קבוע. • ♀♂ • קלאו • שיחה • 16:05, 9 באוקטובר 2012 (IST)

גוף תלת מימדי הוא זה שיש לו אורך רוחב וגובה, (מה שיש לפרידמידה ואין למשולש, או לכדור ואין לעיגול) אז גם לכיפה יש אורך רוחב וגובה! ו/או: מה בין כיפה לכדור?סול במול - שיחה 19:55, 9 באוקטובר 2012 (IST)

בעצם- הבנתי. הכיפה היא רק ה"קליפה", ואילו לכדור יש גם "תוך". תודה!סול במול - שיחה 19:56, 9 באוקטובר 2012 (IST)

בדיוק. חשבתי בנתיים על הסבר אחר. גם אם תיקח מלבן מנייר ותדביק את 2 הקצוות שלו זו לזו ותקבל גליל עם "נפח", הנייר עדיין הוא יריעה דו מימדית. • ♀♂ • קלאו • שיחה • 20:14, 9 באוקטובר 2012 (IST)

בעקבות שאלתך ראיתי שבערך כדור, הכדור מוגדר בטעות כ-ספירה. יתוקן. תודה. • ♀♂ • קלאו • שיחה • 20:20, 9 באוקטובר 2012 (IST)

נראה לי שהמילה גוף לא מתאימה לכיפה. אני צודק? סול במול - שיחה 20:32, 9 באוקטובר 2012 (IST)

אם אתה מתכוון לכך שב"גוף" הכוונה לרוב לאובייקט תלת מימדי וכיפה היא משטח דו מימדי, אז אתה צודק. • ♀♂ • קלאו • שיחה • 20:40, 9 באוקטובר 2012 (IST)

למה שלא יתאים? אין סיבה להפלות על בסיס ממדי. דניאל • תרמו ערך 21:43, 9 באוקטובר 2012 (IST)

חלילה להפלות. התכוונתי למשמעות בשפת היוםיום. • ♀♂ • קלאו • שיחה • 21:53, 9 באוקטובר 2012 (IST)

אחד חלקי הסתברות

מה המשמעות המתמטית/פיזיקלית של פונקציה שהיא $1/\rho$, כאשר $\rho$ פונקציית צפיפות הסתברות. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

חסר משמעות. דניאל • תרמו ערך 23:13, 9 באוקטובר 2012 (IST)

זה תלוי במשמעות של P. אם המשמעות של P היא היחס המספרי הקיים - בין כמות ההתרחשויות של האירוע בעל ההסתברות P - לבין כמות ההתרחשויות של האירועים שבמרחב המדגם, אז המשמעות של "אחד חלקי P" היא היחס המספרי הקיים - בין כמות ההתרחשויות של האירועים שבמרחב המדגם - לבין כמות ההתרחשויות של האירוע בעל ההסתברות P. סמי20 - שיחה 18:18, 18 באוקטובר 2012 (IST)

נובל בפיזיקה 2012

הועבר מויקיפדיה:הכה את המומחה

ברמה של סטודנט לפיזיקה שלמד קוונטים: על מה קיבלו פרס נובל ב-2012? 109.64.244.163

רצוי שתעיין קודם בפרס נובל לפיזיקה, כולל בערכים העוסקים בשני חתני הפרס לשנה זו, ומהם נסה למקד שאלות. בנצי - שיחה 01:12, 10 באוקטובר 2012 (IST)

נמקד את השאלה: מה זה "שיטות ניסיוניות פורצות דרך המאפשרות מדידה ומניפולציה של מערכות קוואנטיות פרטניות." 109.64.244.163 07:49, 10 באוקטובר 2012 (IST)

מרחק מהשמש

הועבר מויקיפדיה:הכה את המומחה

כדור הארץ לא נע במעגל אלא באליפסה. ולכן המרחק של השמש מכ"א משתנה. האם מרגישים הבדלי טמפרטורה בכדור הארץ בעקבות הפרשי המרחק? נגדיר "מרחק" כאורך הישר המחבר את מרכז השמש למרכז כדור הארץ ברגע מסוים.

החלפת עונת נובעת בזווית חשיפה שונה לקרינת השמש ולא מהמרחק, נכון? האם המרחק כן משנה משהו?109.64.187.16 12:50, 10 באוקטובר 2012 (IST)

ראה ערך אפהליון ופריהליון.--ניצן - שיחה 14:10, 10 באוקטובר 2012 (IST)

זה גורם די זניח כי המסלול הוא דמוי עיגול. למען האמת בחורף חצי הכדור הצפוני נמצא קרוב יותר לשמש.Exx8 - שיחה 21:37, 10 באוקטובר 2012 (IST)

דמוי מעגל. עיגול הוא השטח הכלוא בתוכו. בנצי - שיחה 01:56, 11 באוקטובר 2012 (IST)

אלגוריתם ניווט של נמלים

שלום. היכן אפשר למצוא פסאודוקוד של Ant colony optimization algorithm, כמו זה שמוצג כאן? 94.159.184.133 18:03, 10 באוקטובר 2012 (IST)

סינגולריות כבידתית והמפץ הגדול

הועבר מויקיפדיה:הכה את המומחה

לפי מה שראיתי בערך המפץ הגדול היקום התחיל מנקודה בשם סינגולריות כבידתית, אבל לא מצאתי הסבר על איך הנקודה הזאת נוצרה. מישהו יכול להסביר / להפנות אותי לאתר עם הסבר? Someone1234 - שיחה 21:28, 10 באוקטובר 2012 (IST)

המודלים המתמטיים שמתארים את היקום נעצרים בנקודה הזו. הם אינם מתארים את מה שקדם לה, אם היה מה שקדם לה. ישנן תאוריות רבות באשר למה יצר את המפץ הגדול או האם לשאלה הזו יש בכלל משמעות, אבל בכלים הקיימים כיום לא ניתן לאשש או להפריך אף אחת מהן. דניאל • תרמו ערך 21:33, 10 באוקטובר 2012 (IST)

מה גודל הנקודה הזאת (סינגולריות כבידתית)? Someone1234 - שיחה 21:46, 10 באוקטובר 2012 (IST)

היא נקודה ולכן אין לה מימדים. GHA - שיחה - למען החלום, למען השלום, אמצו עוד היום ערך יתום! 21:53, 10 באוקטובר 2012 (IST)

לא מדויק. היא נקודה סינגולרית, לא נקודה גאומטרית. התפיסה הבסיסית, כפי שלמדתי אותה מאסטרופיסיקאים בעלי שם, היא שגודלה היה אינסופי. גורם הסקאלה, אמנם, שואף לאפס. משה פרידמן - שיחה 22:10, 10 באוקטובר 2012 (IST)

ותשובה נכונה אך נטולת תשובה היא שהיה לה רדיוס שוורצשילד... eman • שיחה • ♥ 22:24, 10 באוקטובר 2012 (IST)

לגבי השאלה הראשונה (איך הנקודה "סינגולריות כבידתית" נוצרה?) - אין לכך תשובה? הרי לא ייתכן שהיא הייתה קיימת תמיד.. או שכן? ואם כן, איך זה יכול להיות? Someone1234 - שיחה 22:36, 10 באוקטובר 2012 (IST)

סטיבן הוקינג דן רבות בשאלה זו. תוכל למצוא תשובות בספריו. בכלליות הוא אומר שלא היה "לפני" כי זו נקודה בה התחיל הזמן. נורא קשה לדמיין מה זה "לא קיים לפני", אבל זה בעיקר בגלל שהתפיסה שלנו של הזמן מטעה אותנו. הייתה פה שאלה לפני כמה זמו שבה הזכירו את הדימוי שהוא משתמש בו בהרצאות מול הקהל הרחב: לשאול "מה היה לפני המפץ הגדול" זה כמו לשאול "מה נמצא צפונית לקוטב הצפוני". תחשוב על הדימוי. Corvus,(שיחה) 23:14, 10 באוקטובר 2012 (IST)

התפיסה הפסיכולוגית שלנו היא שהזמן זה משהו שזורם כל הזמן, אבל אם חושבים על כל המרחב זמן כמשהו שקיים כמקשה אחת ולא משתנה לא קשה לדמיין שמעולם לא נוצר ואין לו סיבה. דניאל • תרמו ערך 09:43, 11 באוקטובר 2012 (IST)

זה פשוט לא מסתדר.

1. למה שהנקודה הזאת תיווצר פתאום? גם אם אין שום כלום לפניה היא צריכה שמשהו יגרום לה להיווצר.

2. אם הנקודה הזאת הייתה קיימת תמיד ופתאום אירע ה"פיצוץ" של המפץ הגדול אז מה גרם לנקודה "להתפוצץ"?

לגבי האפשרות השניה - זה פשוט לא נראה לי הגיוני שנקודה כלשהי תתקיים בלי שמשהו אחר יגרום לה להיווצר.

Someone1234 - שיחה 20:33, 11 באוקטובר 2012 (IST)

זה לא שהיה שום דבר לפני המפץ, זה שאין דבר כזה "לפני" המפץ. הזמן עצמו נוצר במפץ. ואולי המילה "נוצר" מטעה כאן כי היא מעידה על משהו שלא היה ואחר כך היה. אבל זה לא המקרה. עליך לחשוב על הזמן כאילו הוא כיווןן תנועה במרחב, בדיוק כמו צפון-דרום ולמעלה-למטה. המרחב כולל הזמן הוא ארבע ממדי והיקום הוא עצם ארבע ממדי שיש לו גבולות. אחד הגבולות הללו הוא המפץ הגדול, אבל הוא לא שונה בשום צורה מקודקוד של משולש שמסמן את סוף המשולש במרחב דו ממדי. דניאל • תרמו ערך 20:55, 11 באוקטובר 2012 (IST)

אני אשאל את זה כך: המפץ הגדול אירע לפני 13.7 מיליארד שנה (לפי הערך המפץ הגדול). מה היה לפני 13.8 מיליארד שנה?

עוד משהו - מה יש מעבר ליקום? הכוונה היא שנניח והייתה יכולה לטוס חללית אל "קצה היקום" (צורת היקום היא כדור, נכון?), לאן היא הייתה מגיעה לאחר חציית הגבול?

Someone1234 - שיחה 02:45, 12 באוקטובר 2012 (IST)

אתה מתעקש על אותה צורת מחשבה שאמרו לך שהיא בעייתית. זה לא מפתיע במיוחד, לאור העובדה שאתה כמוני- בן אדם. אנחנו רגילים לתחושת זמן מסוימת ולכן קשה לנו מאוד לקבל תופעות כמו טרנספורמציות לורנץ ותורת היחסות הפרטית. לא היה קיים 13.8 מיליארד שנה (בהנחה שחישבנו נכון את גיל היקום והוא באמת 13.7), כי לא היה זמן. הזמן עצמו התחיל במפץ הגדול. בערך כמו לשאול: אני נמצא 10 קילומטר מהקוטב הצפוני. אם אני אלך 15 קילומטר צפונה, כדור הארץ יגמר? Corvus,(שיחה) 08:53, 12 באוקטובר 2012 (IST)

זה פשוט לא ייתכן. איך הזמן יכול "להיווצר"? אתם מתכוונים לכך שהמרחב-זמן נוצר במפץ הגדול, אני מניח, אבל ניתן לומר שאם עכשיו היו חוזרים אחורה בזמן עד למפץ הגדול וממשיכים עוד היו מגיעים ל"לפני המפץ הגדול". הכוונה:

? <--- 13.7- מיליארד שנה .. <--- .. 1000- .. <--- .. 0 .. <--- .. 1000 .. <--- .. 2012

שאלה שאולי תחדד את השאלות שלי - האם יכול להיות שהיו עוד הרבה דברים לפני שהיקום נוצר, ושבעצם יש הרבה יקומים וכל "קבוצת יקומים" נמצאת במרחב כלשהו (כמו שהיקום מכיל בתוכו כוכבים, גלקסיות וכו') והמרחב הזה נמצא בתוך עוד מרחב שמכיל כמה מרחבים כאלו וכו' וכו' עד אינסוף?

הנה תרשים שיסביר את כוונתי: (באיור מורחב יותר כל מרחבי ה-Y אמורים להיות במרחב Z וכו')

       ------------------------------------------------------------------------
       |                                                                        |
       |   ----------------------------------------------------------------     |
       |  |                ------------      ----------     ----------     |    |
       |  |               ( היקום שלנו )    ( יקום אחר )   ( יקום אחר )    |    |
       |  |   מרחב         ------------      ----------     ----------     |    |
       |  |  כלשהו (X)                                                     |    |
       |  |  מעבר                ----------           ----------           |    |
       |  |  ליקום              ( יקום אחר )         ( יקום אחר )          |    |
       |  |                      ----------           ----------           |    |   
       |  |                                                                |    |
       |   ----------------------------------------------------------------     |
       |                                                                        |
       |                              מרחב Y                                    |
       |                                                                        |
       |   ----------------------------------------------------------------     |
       |  |                ------------      ----------     ----------     |    |
       |  |                ( יקום אחר )     ( יקום אחר )   ( יקום אחר )    |    |
       |  |   מרחב         ------------      ----------     ----------     |    |
       |  |    X                                                           |    |
       |  |   אחר                ----------           ----------           |    |
       |  |                     ( יקום אחר )         ( יקום אחר )          |    |
       |  |                      ----------           ----------           |    |   
       |  |                                                                |    |
       |   ----------------------------------------------------------------     |
        ------------------------------------------------------------------------

Someone1234 - שיחה 18:19, 12 באוקטובר 2012 (IST)

אתה שואל שאלה במדע או מדע בדיוני? הסבר של יקומים מרובים, תת-יקומים, גורי יקומים נראה יפה לספר מדע בדיוני. אבל אם אתה רוצה תשובה מדעית, אני חושב שקיבלת ממני ומדניאל תשובות. הכשל שאתה נתקל בו הוא שאתה מניח לכל רגע היה רגע לפניו ושהזמן הוא אבסולוטי. שני הטענות האלא לצערנו הרב שגויות. אל תחשוב שהשאלות שלך לא מטרידות את הקוסמולוגים, זה חלק מהעבודה שלהם לשבור את הראש בניסיון לענות לזה. לגבי להמשיך בשרשרת עד למפץ הגדול והאלה (מה סימנת בחץ לסימן שאלה): זה בדיוק כמו לשאול "לאיזה כיוון נגיע אם נלך צפונה מהקוטב הצפוני"(דימוי שהזכרתי מספר פעמים ואתה מתעלם ממנו). פשוט אין, לא קיים משהו צפונית לקוטב הצפוני. Corvus,(שיחה) 18:33, 12 באוקטובר 2012 (IST)

קיימים לכך הרבה הסברים מעולים, שקודמיי ציינו פה. הם גם הזכירו משהו מאוד נכון ושכדאי לך לקחת בחשבון. אנחנו פשוט לא יודעים. אף מדען לא הצליח להוכיח בצורה ניסויית שמה שהוא אומר נכון.הייתי ממליץ לך לעיין בטיעון הפסימי של הפילוסופיה בדבר תיאוריות לא בשלות.

הוקינג הוא מדען מוכשר ואני בטוח שהתיאוריה שלו היא מיטב הידע האנושי בתחום הנ"ל כרגע. אך לרוע המזל, מבחינה סטטיסטית הכי סביר שהוא טועה.Exx8 - שיחה 16:19, 13 באוקטובר 2012 (IST)

לאיזו תיאוריה של הוקינג אתה מתכוון? ול Corvus - מי אמר שהזמן לא אבסולוטי? Someone1234 - שיחה 18:47, 13 באוקטובר 2012 (IST)

אלברט איינשטיין אמר. ראה תורת היחסות הפרטית Corvus,(שיחה) 18:59, 13 באוקטובר 2012 (IST)

נכנסתי לערך ולא מצאתי. תוכל לציין את המיקום בערך או לכתוב כאן את ההוכחה? Someone1234 - שיחה 20:25, 13 באוקטובר 2012 (IST)

הפסקה "שעון במערכת הנעה במהירות קבועה והתארכות הזמן", למרות שנראה שתאלץ לקרוא גם את הפסקה לפני כן בשבי להבין. לא אבסולוטי פירושו "תלוי צופה". Corvus,(שיחה) 20:33, 13 באוקטובר 2012 (IST)

עבודה שלילית

בהקשר של תרמודינמיקה: מתי עבודה מוגדרת שלילית ומתי חיובית? ולמה. נניח שהמערכת שאני מנתח זה גם מתפשט/מתכווץ. 109.67.193.85 20:49, 10 באוקטובר 2012 (IST)

עבודה זה דרך של מעבר אנרגיה. אם יש מערכת שנפחה גדל (אל מול לחץ חיצוני) העבודה עליה היא שלילית, והעבודה שהיא עושה על הסביבה חיובית. אם אני זוכר נכון, בתרמו בד"כ מה שחשוב זה העבודה על המערכת (לכן כשהיא מתפשטת, היא שלילית, כלומר W=-pdV)

למה? כי אם תחשוב על בוכנה שרק דופן אחת שלה זזה, כשהמערכת מתפשטת הכוח החיצוני, שהסביבה עושה על הדופן הנעה, פועל בכיוון שמתנגד לתנועה, לכן עושה עבודה שלילית.

לעומת זאת, הכוח שהגז בבוכנה עושה על הדופן הוא עם כיוון תנועתה, לכן הוא עושה עבודה חיובית. eman • שיחה • ♥ 21:43, 10 באוקטובר 2012 (IST)

רמת פרמי

יש איזה מקום שרשמו רמת פרמי כך: $E_{f}^{(2)}$. מה המשמעות של ה2 הזה? 109.67.193.85 09:38, 11 באוקטובר 2012 (IST)

התוכל להביא את הביטוי השלם, או אף לצטט את כל הפיסקה המתייחסת אליו, כדי לראות את ההקשר ? תודה. בנצי - שיחה 22:56, 11 באוקטובר 2012 (IST)

התפלגות פרמי דיראק, נוסחאות

יש סתירה בין פיתרון של תרגילן אחד לבין דף הנוסחאות שלי. כאן רשמתי את ההשוואה. זה נראה כמו עניין של קונבנציות, אבל אני עדיין לא רואה איך אני מגשר על הסתירה. במיוחד מציק לי שבתשובה בסוף יש פקטור 2 לא ברור. השאלה היא "נתון גז ללא אינטראקציות בעל ספין חצי של חלקיקים הנעים על מישור, בטמפ' T=0". לא נתון A, אבל נתונים m, rho. 79.177.225.220 11:08, 11 באוקטובר 2012 (IST)

שאלה אל כל מי שמתמצא במינוחים מתמטיים

יהיו-נא S,R יחסים. אני תמה האם יש דרך יותר תקנית/פשוטה/קצרה/אינטואיטיבית/עדיפה (מחק את המיותר) להגדיר (ע"י R,S) - בין מילולית ובין בסימון מתמטי - את היחסים הבאים:

• { a,(b,c)) | ((a,b),c)∈R) }
• { a,c),(b,d)) | ((a,b),(c,d))∈R)) }
• { a,c),b) | (a,b)∈R and (b,c)∈S)) }

77.126.182.100 15:56, 11 באוקטובר 2012 (IST)

בשלושת המקרים הייתי כותב כפי שכתבת. אם היחסים R,S בעצמם מתקבלים מפעולת הרכבה, אפשר למצוא תאורים שתלויים בהרכבה הזו. עוזי ו. - שיחה 15:02, 12 באוקטובר 2012 (IST)

תודה (לצערי היחסים R,S אינם מתאפיינים בדבר אשר בדיקת קיומו הוצעה על ידיך). 77.126.182.100 15:54, 12 באוקטובר 2012 (IST)

דרגת חופש ריבועית

מה זה "דרגת חופש ריבועית" ובמה היא שונה מדרגת חופש "רגילה" (או איזה עוד יש?)? 79.177.212.73 16:00, 11 באוקטובר 2012 (IST)

ראה ויקיאנגלית. דרגת חופש היא ריבועית אם ניתן לכותבה כ: $E=\alpha _{i}\,\,X_{i}^{2}+\beta _{i}\,\,X_{i}Y$. אני לא יודע מה היתרון. -יונה בנדלאק - שיחה 18:19, 11 באוקטובר 2012 (IST)

שימוש בעקרון של משאבת חום לייצור חשמל

לא מזמן פנה אלי מישהו בבקשת מימון לבניית אב טיפוס של מתקן שבגדול אמור לנצל את העיקרון של משאבת חום לצורך הפקת חשמל. לטענתו היות ומשאבות חום כגון מזגנים הינם בעלי COP של 3 יחידות ויותר ניתן לנצל את העיקרון הנ"ל לייצור חשמל במקום חום, וכך בעצם להנפיק שתי יחידות חשמל מכל יחידת חשמל מושקעת (אני כמובן מעביר את הדברים מאוד בערך שכן אין לי כמעט מושג בפיזיקה).

כמובן שלפני שאני משקיע כסף אני יחפש מומחה בתחום שיתן חוות דעת מקצועית תוך עיון בכלל החומר שהבחור העביר לי, אבל הייתי שמח לדעה כללית האם סביר להניח כי הרעיון הזה יש בו ממש, לפני שאני עושה צחוק מעצמי מול מומחה בתחום. בתודה מראש לעוזרים, אליהו52ק • שיחה 20:18, 11 באוקטובר 2012 (IST)

אפשר להפיק חשמל, למשל, אם מעבירים חום מאיזור חם לאזור קר, כמו למשל ניצול של גייזר או מקור גיאו-תרמי או וולקני אחר. אי אפשר להפיק חשמל תוך כדי קירור חדר. אי אפשר להפיק חשמל ממזגן, הוא צורך חשמל, ולא משנה מה היעילות שלהם או הדירוג האנרגטי שלהם. בגדול מדובר בשטויות ככל הנראה. ‏Setreset • שיחה 11:30, 14 באוקטובר 2012 (IST)

פיזיקה/הסתברות

אני יודע שהסתברות שחלקיק אחד יהיה בעל תנע p הוא $P(p)=c\beta e^{-\beta cp}$, בטה וC קבועים. כלומר הסתברות תלויה בתנע. מה ההסתברות שמתוך מדגם של N חלקיקים (N גדול מאוד) לפחות אחד יהיה בעל תנע p0? אני יודע שזה אחד פחות ההסתברות שלכולם שונים. מה ההסתברות שכולם שונים מp0? 79.182.245.170 21:39, 11 באוקטובר 2012 (IST)

נניח שההסתברות לכך שלחלקיק יהיה תנע p0 היא P, אזי ההסתברות שיהיה לו תנע שונה מ-p0 היא $1-P$. לפי עיקרון הכפל ההסתברות שלכל החלקיקים יהיה תנע שונה מ-p0 הוא $(1-P)^{N}$. ההסתברות שלפחות לאחד יהיה תנע p0 היא משלים של המאורע האחרון ולכן $\mathrm {Prob} ({\mbox{at least one has }}p_{0})=1-(1-P)^{N}$. בברכה, MathKnight (שיחה) 00:01, 12 באוקטובר 2012 (IST)

זו לא הסתברות אלא צפיפות, ולכן התשובה לשאלתך (שצריך כנראה לתקן) היא 0. עוזי ו. - שיחה 14:58, 12 באוקטובר 2012 (IST)

איך מנקדים "מתמר" (חיישן) Transducer

הועבר מויקיפדיה:הכה את המומחה

אשמח לקבל את תשבותך, ואלי גם הסבר בן שורה או שתיים מה זה בדיוק. אנא שילחו לי את התשובה ל- cnaantheaterweb.de. בתודה מראש, כנען.

ראשית, לא מקובל להחזיר תשובות לכתובות פרטיות. כמו-כן, יש לחתום בסוף הפניה או התגובה, באמצעות 4 פעמים ~, או באמצעות סימון העט הכחול בשורת הכלים בראשו של חלון העריכה.

לגבי עניין הניקוד, יש מדור המיועד לכך: ויקיפדיה:יעוץ לשוני.

מתמר אינו חיישן, משום שאין תפקידו לגלות, אלא להפוך צורת אנרגיה אחת לצורה אחרת. למשל, מתקנים פיאזואלקטריים ממירים אנרגיה מכנית לאנרגיה חשמלית. מונח זה משמש גם בביולוגיה מולקולרית של התא , שכן מדובר בהתמרת אות ביוכימית מצורה אחת לצורה אחרת (ראה דף זה). בנצי - שיחה 23:36, 11 באוקטובר 2012 (IST)

מַתְמֵר. סמי20 - שיחה 03:05, 12 באוקטובר 2012 (IST)

איך לנקד? עבור לאתר האקדמיה העברית, בחר "מילון מונחים", הקלד את המילה בעברית או באנגלית, וקיבלת: מַתְמֵר. ‏[kotz]‏ [שיחה] 08:14, 12 באוקטובר 2012 (IST)

מקרר מלא

האם מקרר מלא ועמוס בדברים (לאחר שהם כבר קוררו) צורך יותר אנרגיה ממקרר ריק? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

בדיוק להפיך. קיבול חום של מוצרי מזון גבוהה מזה של האוויר. ולכן הם שומרים על טמפרטורה קובעה ("שומרים על קור" בשפת היום-יום) לאורך יותר זמן. כמו "קרחומים" לציידנית, רק חלשים יותר. ולכן המקרר מלא צריך להשקיע פחות אנרגיה בשביל לשמור על טמפרטורה קבועה. Corvus,(שיחה) 13:32, 12 באוקטובר 2012 (IST)

אותה אנרגיה, כי האנרגיה הנדרשת לשמירה על הקור שווה לאנרגיה שבורחת, והאנרגיה שבורחת תלויה רק בהפרש הטמפרטורות ומבנה דופן המקרר. ‏Setreset • שיחה 11:26, 14 באוקטובר 2012 (IST)

קיבול החום אכן מבדיל בין שני התווכים מבחינת האנרגיה הדרושה לשינוי הטמפ' באותו שיעור, אבל השאלה מתייחסת להשארת המצב של טמפ' סופית השווה בשני המקרים. בנצי - שיחה 17:13, 14 באוקטובר 2012 (IST)

מסכים איתכם. התשובה שלי יכולה יותר להתאים למקרה שבו מכבים את המקרר וממתינים עד שמגיעים לשיווי משקל תרמי עם הסביבה("הקור יצא"). ואז המזון באמת יהיה כמו "קרחום" בציידנית. מקווה שהפעם אני לא מטעה. Corvus,(שיחה) 18:13, 14 באוקטובר 2012 (IST)

אקספוננט

האם וולפראם אלפה צודק כאן? לדעתי זו סדרה הנדסית ולכן זה צריך להיות: א) בחזקת 0 למעלה ולכן סתם 1 במונה. ב) צריך להיות 1 פחות אקספוננט במכנה ולכן הם "איבדו מינוס".

אבל מניסיון, אין הרבה טעויות לוולפראם. מה אני לא מבין? 79.183.214.80 14:02, 12 באוקטובר 2012 (IST)

צדק בהחלט; אם פותחים את הסוגריים במונה ומחלקים את המונה והמכנה ב$e^{-x}$, מתקבל סכום של סדרה הנדסית בת $m+1$ איברים שמנתה $e^{-x}$ ואיברה הראשון 1. סופ"ש נעים, Tomn - שיחה 14:32, 12 באוקטובר 2012 (IST)

אופס. יצאתי טמבל. 79.183.214.80 14:40, 12 באוקטובר 2012 (IST)

חס ושלום! Tomn - שיחה 14:46, 12 באוקטובר 2012 (IST)

על קבוצות פונקציונליות

1)מדוע כל חומצה קרבוקסילית לא מוחשבת ככוהל? מובן לי שההגדרה היא רק הכללה שנועדה לבני אדם, ובכל זאת המולקולה מכילה OH...למה ה-OH לא גורם לקבוצה להנתהג כמו כוהל? 2)לגבי האמינים, האם רק כאשר ה-N מחובר ל-C הקבוצה תחשב לאמינית? אחרת כל מולקולה המכילה חנקן תחשב אמינית. Exx8 - שיחה 13:18, 13 באוקטובר 2012 (IST)

אנטרופיה

האם זה נכון שבתהליך אדיאבטי אין שינוי באנטרופיה? מדוע? 79.179.193.61 16:38, 13 באוקטובר 2012 (IST)

זה נובע מהגדרת האנטרופיה, s = dq/dT. נגזרת של פונקציה קבועה היא אפס. 94.159.184.133 19:18, 13 באוקטובר 2012 (IST)

שאלה בהסתברות או פיזיקה

ישנה קופסה ובתוכה גז בעל N חלקיקים זהים. החלקיקים מפוזרים בכל נפח הקופסה, כולם נמצאים בתנועה(גז). הסתברות לכל קונפיגורציה שווה.

מה ההסתברות שבחצי השמאלי של הכלי ישנם $0.5N+\epsilon$ חלקיקים ברגע נתון? 79.179.193.61 17:08, 13 באוקטובר 2012 (IST)

ההסתברות שחלקיק מסוים נמצא בצד שמאל היא חצי. לכן את ההסתברות ש-k חלקיקים בדיוק נמצאים בצד שמאל אפשר לחשב עם התפלגות בינומית. דניאל • תרמו ערך 17:15, 13 באוקטובר 2012 (IST)

הניסיון שלי נראה לי לא הגיוני. ההסתברות שחלקיק יחיד יהיה בחצי שמאלי הוא 0.5 כי לחלקיק סיכוי שווה להיות בכל מקום. הסתברות שזני חלקיקים יהיו בחצי שמאלי אמור להיות 0.5 כפול 0.5 כי זה מאורעות בלתי קשורים. אז ההסתברות לזה ש$0.5N+\epsilon$ חלקיקים יהיו בחצי שמאלי הוא $0.5^{0.5N+\epsilon }$. אבל זה נשמע מאוד לא הגיוני. ככל שיש יותר חלקיקים יש פחות סיכוי שחצי מהם יהיו חצי השמאלי של הכלי? משהו לא טוב. איך עושים אם התפלגות בינומית? 79.179.193.61 17:19, 13 באוקטובר 2012 (IST)

ההסתברות ש-2 חלקיקים מסויימים יהיו בחצי השמאלי והיתר יהיו איפשהו הוא 0.5 כפול 0.5. מה ההסתברות ש-2 חלקיקים כלשהם יהיו בצד השמאלי והיתר בצד הימני? כל זאת ועוד בערך התפלגות בינומית. • ♀♂ • קלאו • שיחה • 18:42, 13 באוקטובר 2012 (IST)

למשל ההסתברות שיהיה בדיוק חלקיק אחד בצד שמאל הוא $N/2^{N}$ כי יש N קונפיגורציות כאלו מתוך $2^{N}$ הקונפיגורציות האפשריות (של ימין/שמאל). דניאל • תרמו ערך 19:41, 13 באוקטובר 2012 (IST)

(גם כאן) סביר יותר שרוצים לדעת מה הסיכוי שיהיו *לפחות* $(0.5+\epsilon )N$ כדורים במחצית השמאלית, ולא "בדיוק" כך-וכך כדורים. לשם כך רצוי להשתמש בקירוב הנורמלי להתפלגות הבינומית, ולא בהתפלגות עצמה. עוזי ו. - שיחה 11:56, 14 באוקטובר 2012 (IST)

קרינת גוף שחור, שאלה מקצועית

ברכות על פיתחת הכה לענייני מדעים! שאלה מקצועית אפשר לשאול כאן, נכון? הנה כאן: שאלה ופתרונה. אני לא מבין את התשובה.

אני רואה זה מאוד-מאוד מזכיר את חוק סטפן-בולצמן. מה שאני לא מבין זה כל הפקטורים הגאומטריים. מהו המכנה באיבר הראשון? למה ה-4 פאי ואורך המסלול בריבוע ולמה מחלקים בזה? מאפה בה המונה? בהמשך אני רואה זה שטח פני כדור, נכון? אז כנראה שהפקטור אמור לשקף את אזור כדור הארץ החשוף לקרינה? אתם יכולים לנסות לשחזר איך מגיעים לזה? 109.64.249.81 18:46, 13 באוקטובר 2012 (IST)

היי, הפקטורים הגיאומטריים נחוצים: א) לחישוב האנרגיה הכוללת הנפלטת מהשמש ליחידת זמן (לכן המכפלה 4 פאי כפול רדיוס השמש בריבוע); ב) שטף האנרגיה המגיע לכדה"א הארץ (לכן החלוקה ב־4 פאי כפול המרחק בין השמש לכדה"א בריבוע); ג) לחישוב האנרגיה הנפלטת מכדה"א כגוף שחור, לכן שוב מופיעה בו המכפלה 4 פאי כפול רדיוס כדה"א בריבוע. בהצלחה, Tomn - שיחה 19:15, 13 באוקטובר 2012 (IST)

תודה. לא הבנתי את סעיף ב' שלך. מדוע בשביל לחשב את שטף המגיע לכדה"א יש לחלק ב־4 פאי כפול המרחק בריבוע? בנוסף גף סעיף ג' לא למרי ברור. את הפליטה של כדור הארץ מחשיבים בשורה אחרי זה. בשורה הראשונה כ"א הוא רק קולט. 109.64.249.81 19:20, 13 באוקטובר 2012 (IST)

בבקשה. משום שבהנחה שהאנרגיה הקורנת מן השמש נפלטת באופן איזוטרופי (כלומר בשיעור זהה בכל הכיוונים), השטף, שהוא האנרגיה ליחידת זמן ליחידת שטח, יתחלק על פני מעטפת כדורית שרדיוסה הוא מרחק כדה"א מהשמש. וכדי לחשב את האנרגיה הכוללת (ליחידת זמן) הנפלטת מכדה"א, יש לכפול את קבוע סטפן־בולצמן כפול הטמפ. ברביעית בשטח הפנים של כדה"א, כלומר 4 פאי כפול רדיוס כדה"א בריבוע. מה שמופיע בשורה מתחת הוא אמנם האנרגיה הנפלטת מכדה"א, אבל במונחים של טמפרטורת פני השטח של כדה"א. אתה אמור להשוות בין שני הביטויים כדי לחשב את הטמפרטורה המבוקשת. Tomn - שיחה 19:28, 13 באוקטובר 2012 (IST)

אז חסר פקטור 4 בפתרון? במונה יש פאי במקום 4פאי. עדיין לא ברור לי למה מכפילים גם בשטח פני המשמש וגם בשטח פני כ"א. 109.64.249.81 19:42, 13 באוקטובר 2012 (IST)

לא, שים לב שהביטוי האחרון בשורה הלפני אחרונה הוא לא הפתרון, אלא האנרגיה ליחידת זמן (או הספק) הקורנת מכדה"א במונחים של טמפרטורת פני השמש. לא חסר פקטור 4, משום שהוא הצטמצם קודם לכן. את הביטוי הזה יש להשוות לביטוי בשורה האחרונה - ההספק הקורן מכדה"א במונחים של טמפרטורת פני כדה"א. מכאן אפשר לחלץ את טמפרטורת פני כדה"א. כל טוב, Tomn - שיחה 20:04, 13 באוקטובר 2012 (IST)

חוק הפאזות של גיבס

בתרמודינמיקה הגדירו לנו אותו כך: $f=n+1+c-p$, כאשר f מימד השפה, c מספר החומרים השונים, p מספר הפאזות ו-n (פה הבעיה) זה "מספר הדרכים לבצע עבודה". מה זה n? אני לא מבין את "מספר הדרכים". יוצא שבדיאגרמה הידועה זה חייב להיות 1, לא? באיזה מקרים זה שונה?109.67.217.85 09:48, 14 באוקטובר 2012 (IST)

תנאי תהתכנסות

מה התנאי על אלפה בשביל שהאינטגרל $\int {\frac {x^{\alpha -1}}{e^{x}-1}}$ יתכנס? האינטגרל מקבוע גדול מ0 עד אינסוף. 79.179.243.122 13:49, 14 באוקטובר 2012 (IST)

ייתכנס תמיד. אקספוננט מנצח בענק כל פולינום. דניאל • תרמו ערך 19:29, 14 באוקטובר 2012 (IST)

ליקוי לבנה בקוטב

הועבר מויקיפדיה:הכה את המומחה

האם תושבי הקוטב (הצפוני/הדרומי) ראו פעם ליקוי חמה או ליקוי לבנה? (בהנחה שהם לא נסעו לארץ אחרת וראו משם את הליקוי). ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

כן: [1] הפיקנופודיה טובה ממך! אילן שמעוני, - שיחה 20:04, 14 באוקטובר 2012 (IST)

האם במבט מהקוטב הצפוני בחודשי הקיץ, השמש אינה שוקעת, אלא נמצאת סמוך לאופק ונעה ממזרח למערב?

בקוטב ממש אין מזרח ואין מערב. אם תעמוד אבל קצת דרומית לקוטב הצפוני תראה את השמש נעה ממזרח מערב, ואז חוזרת ממערב למזרח (אבל בגובה קצת יותר נמוך).eman • שיחה • ♥ 00:30, 15 באוקטובר 2012 (IST)

השמש נעה במעגל בכיוון השעון, ובשעות ה"אין לילה" היא נעה ממערב למזרח. בשעת חצות השמש נמצאת בזוית הנמוכה ביותר ביחס לקו האופק. בקוטב עצמו אין משמעות לכיוונים מזרח ומערב, כל הכיוונים הם דרום.--ניצן - שיחה 00:34, 15 באוקטובר 2012 (IST)

איך נראית תנועת הירח בקוטב הצפוני? 87.68.162.213 22:47, 14 באוקטובר 2012 (IST)

מצב הירח ישתנה לאורך החודש. בתחילתו ובסופו הוא ייראה יחסית קרוב לשמש, וינוע יחסית באופן דומה. אבל באמצע החודש הוא לא ייראה כלל, כי הוא יהיה בשמים במקום בו השמש נמצאת בחורף. גם אצלנו בקיץ הירח נמצא גבוה בשמים בתחילת החודש, אבל נמוך יותר באמצע החודש. eman • שיחה • ♥ 00:30, 15 באוקטובר 2012 (IST)

פיזיקה סטטיסטית, הצבר הגראנד קנוני

מישהו יכול להסביר לי את המעבר שסימנתי בחץ כתום? אני לא מבין איך עושים את זה. 79.176.220.110 22:33, 14 באוקטובר 2012 (IST)

הם עברו משימוש במשתנה שהוא מספר החלקיקים N, שהולך מ 0 עד M, לM משתנים שהם האיכלוס n, שיכולים להיות 0 או 1.ירון ק. - שיחה 08:13, 27 באוקטובר 2012 (IST)

חום סגולי נפחי

חום סגולי או קיבול חום סגולי מוגדר ככמות האנרגיה הדרושה להעלות במעלה אחת את הטמפרטורה של גרם (או קילוגרם) אחד של חומר כלשהו. נגדיר כחום סגולי נפחי את כמות האנרגיה הדרושה להעלות במעלה אחת את הטמפרטורה של סמ"ק (או מ"ק) אחד של חומר כלשהו (נניח בלחץ אטמוספרי אם מדובר בגז). לאיזה חומר יש את קיבול החום הנפחי הגבוה ביותר? (ניחוש, מדובר במתכת כלשהי עם משקל סגולי גבוה או במלח שלה). Easy n - שיחה 10:33, 15 באוקטובר 2012 (IST)

יתכן וזה יכול לעזור. 109.160.231.46 16:46, 16 באוקטובר 2012 (IST)

גז אידיאלי

אם ישנה מערכת גז אידיאלי בשיווי משקל, ודוחסים אותה בעזרת בוכנה נטולת חיכוך עד נפח מסוים ומשחררים את הבוכנה, האם הבוכנה תתחיל לנוע בתנועה הרמונית? אם ישנו חיכוך, האם הנפח החדש שהמערכת תתפוס בשיווי משקל יהיה בהכרח הנפח שצופה משוואה הגזים האידיאלים, ללא תלות בחוזק כוח החיכוך? :שאלה נוספת: כשאני דוחס את הבוכנה, מה גורם ברמה המולקולרית למולקולות להאיץ? הרי ההתנגשויות עם הקיר\בוכנה נשארות אלסטיות כשהיו, והמהירות לפנני ההתנגשות בקיר אמורה להיות זהה בגודלה למהירות אחרי ההתנגשות בקיר. תודה, 94.159.247.222 14:53, 15 באוקטובר 2012 (IST)

1.כן, תנועה הרמונית. 2. לא, כי החיכוך יעצור את הבוכנה לפני שווי משקל בנקודה שאי אפשר לחזות מראש במקרה אמיתי, וניתן לחיזוי אך תלוי במודל החיכוך בבעיה תיאורטית. 3. מספר ההתנגשויות ליחידת זמן. ‏Setreset • שיחה 09:47, 18 באוקטובר 2012 (IST)

תודה על התגובה. לגבי השאלה השנייה - האם מצב כזה לא אקוויולנטי לתנועה הרמונית עם שיכוך בה בסוף המערכת כן עוצרת על נקודת שיווי המשקל? 94.159.230.168 18:44, 18 באוקטובר 2012 (IST)

רק אם השיכוך מתכונתי (פרופורציוני) למהירות אז זה כך. במקרה אמיתי של בוכנה, החיכוך הדינמי די קבוע ותלוי באופן חלש במהירות, ואפילו אולי קטן עם המהירות, ומה שיעצור אותו בפועל מחוץ נקודת שווי המשקל הוא החיכוך הסטטי. במקרה שהחיכוך נובע רק מהתנגדות האוויר או נוזל, למשל, ואין חיכוך עם דפנות, החיכוך מתכונתי למהירות בחזקה מסוימת ואז אכן יעצור בנקודת שווי המשקל. ‏Setreset • שיחה 17:46, 20 באוקטובר 2012 (IST)

תודה רבה. 109.160.228.226 18:21, 20 באוקטובר 2012 (IST)

שאלה בקוונטים

פיתרון לשאלה בקישור הזה אני לא מבין 2 דברים:

1. למה משולש?
2. למה N עד E שווה למה שרשום (זה מזכיר לי מעט שטח משולש, אבל הצלעות שלו לא ברורות).

תודה לעונים. 79.177.230.196 16:53, 15 באוקטובר 2012 (IST)

1. הנקודות בשירטוט מציינות מצבים. תחשוב לאיזה מצבים יש אנרגיה קטנה או שווה למה שרשום, תראה שתקבל משולש
2. זה שטח של משולש שווה צלעות כמו שמופיע בשירטוט

שים לב שהפיתרון די טיפשי. למעשה מה שחישבו זה את אורך הקו האדום בצורה מאוד מסובכת. ירון ק. - שיחה 10:01, 26 באוקטובר 2012 (IST)

מה פירוש הסימנים של F וN בסטטיסטיקה והסתברות?

יש נוסחה שבה הכמות במונה מסומנת באות f (קטנה) והמכנה מסומן באות N של מה זה ראשי התיבות של האותיות האלה? (אני מבין שזה קיצורים של מילים שונות) 46.210.32.9 20:06, 15 באוקטובר 2012 (IST)

סביר שב-f מתכוונים לשכיחות, וב-N למספר האירועים הכללי (היחס ביניהם הוא הפרופורציה, השווה להסתברות אם מדובר במרחב מדגם סופי). נוסחה שבה כתוב משהו כמו "a=bc" אינה שלמה; צריך להיות "a=bc כאשר b הוא מספר התפוחים, c המחיר לתפוח, ו-a המחיר הכללי". עוזי ו. - שיחה 21:19, 15 באוקטובר 2012 (IST)

עוזי, השאלה היא מה הוא הפתרון של ראשי התיבות באנגלית (ולא מה הכוונה), כלומר איזה מילה באנגלית מייצגת כל אות... 109.253.191.254 16:38, 16 באוקטובר 2012 (IST)

אם אלו אכן שכיחות ומספר, אז אלו קיצורים של Frequency ו-Number. עוזי ו. - שיחה 16:49, 16 באוקטובר 2012 (IST)

שאלה קצרצרה. אלגברה ליניארית

נתון P מטריצת הטלה. הוכח כי P= P פלוס (הופכי מוכלל, הפלוס כביכול בחזקה..). אשמח לעזרה בהוכחה הזאת.. אני יודע שהיא קצרה אבל אני פשוט לא מצליח. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

שאלה קצרה במטריצות הטלה

הועבר מויקיפדיה:הכה את המומחה

נתון P מטריצת הטלה. הוכח כי P=P+ (כביכול p בחזקת + הופכי מוכלל). ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

מערכת השמש

הועבר מויקיפדיה:הכה את המומחה

בתקופה שלפני היום הקצר ביותר בשנה (בחצי הכדור שלנו), זמן זריחת השמש בכל בוקר הוא מוקדם יותר מזמן הזריחה של היום הקודם, וזמן שקיעת השמש בכל ערב הוא מאוחר יותר מזמן השקיעה של היום הקודם. בתקופה שאחרי היום הקצר ביותר - זמן הזריחה מתאחר וזמן השקיעה מתקדם. אבל, התאריך, בו זמן הזריחה הוא המוקדם ביותר, שונה מהתאריך, בו זמן השקיעה הוא המאוחר ביותר. איך זה קורה? האם זה קשור לכך, שהתקופה שמיום השוויון האביבי (21 במרץ) עד יום השוויון הסתווי (22 או 23 בספטמבר) ארוכה בארבעה עד שישה ימים מהתקופה שמיום השוויון הסתווי לזה האביבי (לפי הערך אפהליון ופריהליון ).

שאלה נוספת:

שעת הזריחה המאוחרת ביותר היא בתחילת ינואר, ושעת הזריחה המוקדמת ביותר היא בתחילת יוני. (באותו אופן, שעת השקיעה המאוחרת ביותר היא בתחילת יולי, ושעת השקיעה המוקדמת ביותר היא בתחילת דצמבר.)

במשך 5 חודשים, מתחילת ינואר עד תחילת יוני - בכל יום הזריחה נעשית מוקדמת יותר מאשר ביום הקודם. במשך 7 חודשים, מתחילת יוני עד תחילת ינואר - בכל יום הזריחה נעשית מאוחרת יותר מאשר ביום הקודם.

למה אורך התקופה הדרושה לשינוי שעת הזריחה מהמצב המאוחר ביותר אל המוקדם ביותר, שונה מאורך התקופה הדרושה לשינוי שעת הזריחה מהמצב המוקדם ביותר אל המאוחר ביותר?

שאלה נוספת:

אם משרטטים גרף של שעת חצות היום/הלילה (לפי שעות זמניות), מקבלים שבכל שנה יש לגרף 4 נקודות קיצון. השעה המוקדמת ביותר של חצות היום/הלילה לפי שעות זמניות היא בתחילת נובמבר, והמאוחרת ביותר היא בתחילת פברואר. בנוסף, לגרף יש עוד 2 נקודות קיצון מקומי, באמצע מאי ובסוף יולי, אבל ערכי קיצון אלו הם רק מקומיים.

מה גורם לכך, שערך הקיצון המתקבל באמצע מאי, הוא הרבה יותר מאוחר מערך הקיצון המתקבל בתחילת נובמבר?

(ניסיתי להוסיף קובץ עם תרשים, אבל לא הצלחתי.)

87.68.162.213 06:36, 16 באוקטובר 2012 (IST)

ישנן שתי הגדרות שונות למדידת זמני הזריחה והשקיעה. לפי הערך נקודת השוויון, "לצורך מדידת אורך יום, זריחת השמש מתרחשת כאשר מחצית מגוף השמש נצפה מעל לאופק המזרחי, ושקיעת החמה מתרחשת כאשר מחצית מגוף השמש נצפה יורד אל מתחת לאופק המערבי. בהתחשב בהגדרה זו, אורך היום (והלילה) הוא בדיוק 12 שעות בנקודת השוויון. עם זאת, שכיחה יותר הגדרת יום כמשך הזמן בו אור השמש מגיע אל האדמה בהיעדר מכשולים מקומיים. מאחר שהשמש אינה נקודה אלא דיסקה עגולה, ואור השמש נשבר באטמוספירה ומשתקף בחזרה אל הארץ, היום בהגדרה זו יהיה ארוך יותר מהלילה בכמה דקות (כמעט 14 דקות בקו המשווה, ואף יותר לקראת הקטבים), לכן השוויון הלכה למעשה מתרחש כמה ימים לפני נקודת השוויון האביבית וכמה ימים אחרי נקודת השוויון הסתווית."

לפי הערך אורך היממה, "אורך היממה משתנה באופן מחזורי לאורך השנה (משום שמהירות כדור הארץ במסלולו האליפטי סביב השמש אינה קבועה, וסיבות נוספות) ...". ולפי דף השיחה של ערך זה, "מהירות השמש בשמים מורכבת משתי תנועות: סיבוב כדור הארץ סביב עצמו, שנעשה במהירות קבועה, וסיבוב כדור הארץ סביב השמש, שבגלל אליפטיות המסלול נעשה במהירות משתנה! בינואר (כשכדור הארץ נמצא בפרהליון) מהירות זו היא המהירה ביותר, וביולי היא הנמוכה ביותר. לכן אורך היממה משתנה באופן מחזורי לאורך השנה. (קראתי שיש עוד גורם שמשפיע על כך, אבל לא התעמקתי בכך)."

אבל אני לא בטוח שזה מסביר:

1) למה זמן חצות היום והלילה אינו קבוע?

2) למה התקופה בה שעת הזריחה נעשית מוקדמת היא קצרה בחודשיים מהתקופה בה שעת הזריחה נעשית מאוחרת? (וכן לגבי שעת השקיעה)

3) למה השינוי בשעת הזריחה הוא מהיר יותר באביב מאשר בסתיו, ולעומתו השינוי בשעת השקיעה הוא מהיר יותר בסתיו מאשר באביב.

87.68.161.209 20:43, 22 באוקטובר 2012 (IST)87.68.161.209 20:50, 22 באוקטובר 2012 (IST)

ספקטרוסקופיה של השמש

בניתי ספקטרוסקופ ביתי ממש פשוט (סדק דק +דיסק CD) והוא פועל (בדקתי על נורת פלורסנט וראיתי ממש קווים בדידים). בעיה שכשאני מסכל על אור השמש אני רואה רצף. פשוט אין "קווים" אלא ממש קשת. אני לא כל כך רוצה להסתכל על השמש ישירות (אני לא בטוח שזה שהסדק דק והאור מוחזר מדיסק מגן על העין מנזקי הקרינה) אז אני מסכל על רצפה שממנה משתקף האור, אולי זו הבעיה? אם כך, איך אפשר לפתור אותה?

המטרה של הניסוי היא למצוא ספקטרום פליטה בדיד של השמש וממנו להסיק את ההרכב הכימי שלה (לא באמת- זה סתם ניסוי ביתי. אבל ברעיון). 79.176.233.201 19:28, 18 באוקטובר 2012 (IST)

זהו, שלשמש אין ספקטרום פליטה בדיד. קרינת השמש היא קרינה עם ספקטרום רציף, פחות או יותר של קרינת גוף שחור. היא "נורת להט" תרמו-גרעינית ענקית.

אם כבר, מה שאפשר להבחין בשמש זה דווקא ספקטרום בליעה, כלומר "חורים" בספקטרום, שמתאימים לאורכי גל בספקטרום של אטומים שבלעו חלק מהאור. אבל הבליעה לא חייבת להיות מוחלטת, וגם אם כן, ההפרדה של הספקטרומטר צריכה להיות מספיק טובה בשביל שזה יעבוד. eman • שיחה • ♥ 23:01, 18 באוקטובר 2012 (IST)

קו הבליעה שאני אמור לראות הם של חנקן ואוזון? יכולת ההפרדה היא באמת לא משהו, אבל אולי באמת אפשר לראות טיפה קווים חשוכים. איפה אני יכול להשוות לספקטרום בליעה של הגזים הללו?

ממש אכזבת אותי. אז איך בדיוק אני יכול לבדוק ממה עשויה השמש? אני לא מאמין בשום דבר עד שלא ראיתי אותו בעצמי. איזה ניסוי יתן לי את ההרכב או לפחות את "היסוד הדומיננטי" בשמש? 79.179.219.184 11:39, 19 באוקטובר 2012 (IST)

אקו דופלר

אני יודע מה זה אפקט דופלר. אבל מה זה (השיטה הרפואית) "אקו דופלר"? 79.179.219.184 11:55, 19 באוקטובר 2012 (IST)

לא בטוח שאני יודע למה התכוונת אבל למשל באקו לב ניתן בעזרת אפקט דופלר לזהות את כיוון תנועת הדם שנכנס או יוצא מהלב ולצבוע על המסך את העורקים והורידים בצבע שונה כדי לקבל תמונה ברורה יותר. Assafn • שיחה 14:52, 22 באוקטובר 2012 (IST)

בעל מטען חשמלי

איך אפשר להסביר הכי טוב את ההגדרה של "בעל מטען חשמלי" לאדם שלא יודע מה זה חשמל? אני רוצה להסביר לו שהאטום הוא "בעל מטען חשמלי" (חיובי או שלילי זה לא משנה בינתיים). איך אפשר להסביר את זה לילד בגן מה זה המטען החשמלי (מהות החשמל, אנרגיה, אש או מה?)? 46.210.93.186 14:25, 19 באוקטובר 2012 (IST)

לא צריך להסביר מה זה מטען חיובי או שלילי. אם כן, אז אפשר לדמות את זה למגנט שמושך אליו דברים ממגנטים, ככה צד אחד של המעגל מושך אליו דברים/אלקטרונים מהצד השני. אני הייתי מנסה להסביר שמדובר על אבק קטן מאוד שלא רואים כי הוא זז מהר מאוד ובגלל זה נוצר אור/אש וכדומה. -יונה בנדלאק - שיחה 15:33, 19 באוקטובר 2012 (IST)

א. מלבד הדוגמא הטובה של 'מגנטים', אתה מנסה להימנע משימוש במושגים מורכבים לגיל זה, במחיר של שימוש במושגים ותופעות אחרות, מורכבות לא פחות, וחלקן אף יותר.

ב. בגיל זה, אפשר להסתמך על חוויות והתנסויות המוכרות לו. 'גוף טעון חשמלית' נושא עמו תכונה פנימית, ולזו יש שתי צורות מנוגדות (אין צורך בשלב זה לדבר על 'פלוס' ו'מינוס' מאחר ובגיל זה המינוח עדיין לא מוכר קוגניטיבית), כאשר גופים בעלי תכונות מנוגדות - נמשכים זה לזה, וגופים בעלי תכונה דומה - דוחים זה את זה. כאן אפשר להשתמש באנלוגיה לתופעה אחרת - קטבים מגנטיים. מה שטוב בתופעה הזו, למרות שהיא מורכבת בהרבה מהתופעה החשמלית, הוא העובדה שניתן להראות בקלות קטבים נמשכים וקטבים דוחים. עם זאת, צריך להבהיר שזו רק תופעה דומה, ולא זהה, כדי לא לקבע זהות שגויה. בנצי - שיחה 00:55, 20 באוקטובר 2012 (IST)

"אם אתה לא יכול להסביר את זה לילד בן ארבע, כנראה שאתה לא מבין את הנושא בעצמך" (אלברט איינשטיין) נוסחה אחרת: "אם אתה רוצה לדעת אם הבנת דבר מסויים בעצמך, אתה צריך לדעת להסביר אותו לילד בגיל 6" (אלברט איינשטיין) 46.210.181.134 00:59, 21 באוקטובר 2012 (IST)

האם אין כאן קצת הגזמה?

לפי "חדשות ואקטואליה" שראיתי באתר זה, מצוטט ממעריב, אוהדים הצליחו להרעיד את היציעים בעוצמה של 6.4 בסולם ריכטר. זה נראה לכם סביר? על פי הערך "סולם ריכטר" בויקי אנגלית מדובר בכמות אנרגיה הגדולה בערך פי שלוש מזו ששוחררה בהפצצת נגאסאקי. נראה לי שחלה כאן איזו טעות. משה פרידמן - שיחה 14:05, 21 באוקטובר 2012 (IST)

אל תאמין לכל מה שאתה קורא בעיתון. גם אם הם רקעו ממש חזק, אז הרי שההפרעה היא מקומית. בניגוד לרעידת אדמה שהטווח שלה גדול מאוד.

האם סכמה כימית זו נכונה?

מהחלק הגדול לקטן ביותר: אטום מורכב מפרוטונים נייטרונים ואלה מורכבים מקווארקים. האם יש משהו יסודי יותר שמרכיב את הקווארקים או שהקווארקים הם חומר יסודי? 176.13.81.116 16:26, 21 באוקטובר 2012 (IST)

הפיסיקה המקובלת כיום לא מניחה חלקיקים המרכיבים את הקוורקים. לגבי האטום מורכב כמובן גם מאלקטרונים, והגרעין לא מורכב רק מקוורקים, אלא ממכלול שלם של חלקיקים. משה פרידמן - שיחה 17:46, 21 באוקטובר 2012 (IST)

אני דווקא לא חושב שיהיה נכון לומר שהגרעין לא מורכב רק מקווארקים. נכון שהקווארקים בפרוטון ובנייטרון מוחזקים ע"י גלואונים, ושגם יכולות להתרחש אינטאקציות עם ניטרינואים. אבל ממה הגרעין מורכב, הייתלי אומר מפרוטונים ונייטרונים, שכל אחד מהם מורכב משלושה קווארקים. eman • שיחה • ♥ 18:30, 21 באוקטובר 2012 (IST)

אני קצת מתבייש לומר שעל אף שזה בדיוק מה שאני חוקר כרגע, ההבנה התיאורטית שלי בנושא די מוגבלת. בכל זאת, מה שאני מבין הוא שהתפיסה הזו נחשבת למיושנת במקצת, ואיננה מתיישבת עם התוצאות הניסיוניות. משה פרידמן - שיחה 20:18, 21 באוקטובר 2012 (IST)

למה אתה מתכוון? eman • שיחה • ♥ 21:14, 21 באוקטובר 2012 (IST)

ראשית, כנסיונאי שחוקר את הפרוטון מעולם לא העליתי על דעתי להתייחס לגלואונים באופן פחות "קיים" מאשר לקווארקים. אני נזהר כי אולי זו פרשנות לא נכונה שלי, אבל בניסוי פיזור אתה מפזר עליהם, הם נושאים תנע ומסה, והם חלק מאפיון המבנה של הפרוטון (או הגרעין), מה שנקרא Generalized Parton Distribution. מעבר לכך, מודלים של נוקלאון כוללים גם פיונים (ראה למשל Cloudy bag model). משה פרידמן - שיחה 21:39, 21 באוקטובר 2012 (IST)

נתחיל מהסוף. ללא ספק אתה מומחה יותר גדול ממני בנושא, ואני לא מכיר את התיאוריות האלה. אבל הרי גם הפיונים מורכבים מקווארקים. (אבל זה כן מתקן את מה שקבעתי לגבי שלושה קווארקים)

ולגבי הגלואונים. אני כמובן לא כופר בקיומם. אבל השאלה האם אנחנו יכולים להתייחס אליהם כאל מרכיב. ואם כן, האם גם נצטרך להתייחס לפוטונים כאל מרכיב של האטום? אבל זה כבר יותר שאלות של הגדרה. eman • שיחה • ♥ 22:32, 21 באוקטובר 2012 (IST)

קודם כל, כפי שציינתי למעלה, אני ממש לא מומחה. זה לא יאומן כמה מהר נזרקתי לסבך של העבודה הנסיונית, ולא מצאתי את הפנאי להבין לעומק מה אני חוקר בכלל. לגוף הדברים, ההבנה הנוכחית שלי היא בדיוק כמו שאמרת, שזו שאלה של הגדרה. אבל בניגוד לאטום, שם יש הפרדה מאוד ברורה (למשל של סדרי גודל, אחוז המסה וכו') בין אבני היסוד לבין האינטראקציות, בגרעין זה לא המצב. מדובר בחומר דחוס מאוד, שיש בו משמעות לכל המכלול הנ"ל, באופן שלא ברור לי על איזה בסיס ניתן לומר שקווארק הוא ה"מה שיש" והגלואון הוא ה"אינטראקציה". משה פרידמן - שיחה 22:45, 21 באוקטובר 2012 (IST)

על סמך זה שהגלואונים נוצרים ונעלמים, ומספר הקווארקים (תקן אותי אם אני טועה, ומה שכתבת על הפיונים אולי אומר שאני טועה) קבוע. eman • שיחה • ♥ 23:07, 21 באוקטובר 2012 (IST)

מספר הקווארקים לא קבוע, ולא רק בגלל הפיונים. לפי מה שהבנתי תהליך יצירת זוגות בתוך הגרעין איננו זניח. מעבר לכך, מבחינת מסת הנוקלאון, 3 קוורקים זה ממש מעט. זה אומר שקשה להתעלם מהגלואונים בתור גורם משמעותי במבנה הנוקלאון, גם אם מספרם אינו קבוע. משה פרידמן - שיחה 23:18, 21 באוקטובר 2012 (IST)

נכון. מסת הקוורקים היא חלק קטן ממסת הנוקלאון. אבל אני מייחס את זה לאנרגית הקשר. האם זה אקוויוולנטי ללייחס את זה לגלואונים? לא בטוח. eman • שיחה • ♥ 00:59, 22 באוקטובר 2012 (IST)

על פניו הייתי אומר שאנרגית הקשר אמורה להקטין את מסת הנוקלאון, לא להגדיל. אבל נראה לי שאני צריך לבדוק יותר לעומק את הדברים לפני שאני ממשיך. משה פרידמן - שיחה 06:45, 22 באוקטובר 2012 (IST)

זו איננה 'סכמה כימית'. כל מה שמתחת לרמה האטומית, בדר"כ איננו בתחום עיסוקה של הכימיה, בודאי לא שאלת ההרכב שאתה מעלה. בנצי - שיחה 23:32, 21 באוקטובר 2012 (IST)

בכרומודינמיקה קוונטית על סריג מתייחסים לנוקלאונים כבעלי 3 קווארקים של ערכיות וזהו. כל שאר המרק נמצא בים הקוונטי, ולא ממש "קיים" באותו האופן, הם כולם וירטואליים. ‏Setreset • שיחה 06:48, 22 באוקטובר 2012 (IST)

קשה לי לקבל את הפרשנות הזו, משום שאינני מבין באיזה מובן שלושת הקווארקים הנ"ל יותר קיימים מכל שאר החלקיקים הוירטואלים. לא לאלה ולא לאלה קיום בפני עצמם, ואפילו הזהות של קווארקי הערכיות בכלל לא נשמרת. זוגות של קווארקים ואנטי קווארקים נוצרים ונעלמים כל הזמן, ובכלל לא ברור לי שיש שם שלושה קווארקים ספציפיים ששומרים על עצמם בכל הבלאגן ששורר שם, אם בכלל יש לזה משמעות. בסופו של דבר בניסוי אתה מודד עשרות קווארקים, והגלואונים הם אלו שתורמים את מירב המסה של הפרוטון. בפועל הנוקלאון הוא יישות פיסיקלית, שתכונותיה הסטטיות והדינמיות נקבעות על ידי כל אוסף החלקיקים הנ"ל. משה פרידמן - שיחה 08:48, 22 באוקטובר 2012 (IST)

In principle, lattice gauge theory should have the potential to describe QCD directly from the underlying Lagrangian. However, these calculations have yet to be restricted to the “quenched approximation”, i.e. initial configurations of 3 valence quarks. This is a bad approximation for light quarks, because the Goldstone mechanism creates plenty of sea quarks, and therefore the calculations are typically performed for massive quarks, mq ≈ 100 MeV, and then extrapolated to the small u and d quark masses. -arXiv:nucl-th/0003061v1 28 Mar 2000 משה פרידמן - שיחה 08:57, 22 באוקטובר 2012 (IST)

הציטוט הזה עושה בלגן וגם מיושן. הוא מדבר על אילו קוורקים ניתן או לא ניתן למדל בתוך הים, ולא על מה נמצא בערכיות של נוקלאון. מה שהיה המצב אז הוא שיכלו למדל רק את הקוורקים בערכיות וזה קירוב לא טוב. כיום יודעים למדל את כל הקוורקים (נכון שבמסות גבוהות יותר מהאמיתיות), אבל עדיין בערכיות יושבים שלושת הקוורקים הנומינליים. זה נכון שבתוך הנוקלאון יש בלגן גדול, שהוא לא כזה מבולגן אלא נקבע ע"י הלגרנזיאן, אבל יש משמעות מכרעת לקוורקים הוולנטיים, שהם בעצם קובעים מהו החלקיק. הם בעצם "תנאי השפה" של הבעיה, אחרת יש רק ים של QCD בלי שום מגבלה ובלי ממשות. ‏Setreset • שיחה 14:11, 22 באוקטובר 2012 (IST)

לא טענתי לרגע שאין משמעות לקווארקי הערכיות, אבל להגיד שהפרוטון מורכב רק מהם? זו בוודאי לא השפה המקובלת בסביבה שאני נמצא בה. כשמדברים על הרכב או מבנה הפרוטון, מדברים על הרבה יותר מזה. משה פרידמן - שיחה 16:53, 22 באוקטובר 2012 (IST)

אז מה יוצא מהדיון כאן? האם מוסכם על כולם שהקוורקים הם חלקיק יסודי שלא ניתן לחילוק יותר (בדומה לאלקטרון)? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

כן. הדיון הוא איך לתאר את המבנה הפנימי של הפרוטונים והנייטרונים. ‏Setreset • שיחה 23:07, 22 באוקטובר 2012 (IST)

על סמך מה אתה קובע שזהו סוף פסוק, אם היבנתי נכון את תשובתך ? נכון לעת עתה, אין יודעים על מבנה יסודי יותר. אגב, גם התקציבים שידרשו לבדוק זאת בדור הבא, דמיוניים לחלוטין. בנצי - שיחה 04:02, 23 באוקטובר 2012 (IST)

תודה לכולם על ההשתתפות בדיון, היה דיון פורה ומעניין. (אם למישהו יהיה משהו להוסיף הוא מוזמן לעשות זאת) מוטיבציה - שיחה 23:15, 23 באוקטובר 2012 (IST)

המסלול האליפטי כל כדור הארץ

מהו המוקד השני של אליפסת מסלול כדור הארץ מלבד השמש? אביעד‏ • שיחה 22:13, 21 באוקטובר 2012 (IST)

מכיוון שהאקסצנטריות של המסלול היא בערך 0.0165, המרחק בין שני המוקדים הוא כ-2.5 מליון קילומטר. מרכז השמש הוא אחד מהם, והשני נמצא בערך 2 מליון קילומטר ממנה. חם שם. עוזי ו. - שיחה 22:38, 21 באוקטובר 2012 (IST)

שאלה בפיזיקה: איזה חלקיקי אטום יכולים להתקיים בפני עצמם?

האם פרוטון נייטרון או אלקטרון או קווארק יכולים להתקיים בפני עצמם? ושאלה נוספת, האם כל החלקיקים האלה מוחשיים וא"כ באיזו דרך הם מוחשיים? (או בקיצור, איך מגדירים את מוחשיותם)109.253.246.47 16:35, 22 באוקטובר 2012 (IST)

פרוטון נויטרון ואלקטרון יכולים להתקיים בפני עצמם. בפועל בדרך כלל מהר מאוד הם יימצאו שותפים להפוך להיות חלק מאטום אחר (או מבנה כימי מורכב יותר). הנויטרון, במידה וישרוד מספיק זמן, יתפרק לאחר כ 10 דקות בממוצע. הקווארקים לא יכולים להתקיים בפני עצמם. לא יודע איך להגדיר מוחשות, אבל, למשל, אם לא תזהר אלקטרונים ופרוטונים מהירים, או נויטרונים איטיים, יכולים להרוג אותך. משה פרידמן - שיחה 16:49, 22 באוקטובר 2012 (IST)

שלום משה, לגבי שאלה ותשובה 2, כתבת שאינך יודע איך להגדיר מוחשות. אז אשאל בצורה אחרת: באיזה חוש מהחושים חשים את החלקיקים הנ"ל? (חוש הראייה, השמיעה, ההרחה, המישוש, הטעם). ולגבי המשפט שכתבת: "אם לא תזהר אלקטרונים ופרוטונים מהירים, או נויטרונים איטיים, יכולים להרוג אותך." ניסיתי להבין מה פשט הדברים ולא הצלחתי להבין למה התכוונת. בנוסף, כיצד ניתן להזהר מהם ומתי צריך להזהר מהם ואיך ייתכן שרוב הציבור שאינו מודע לחלקיקים אלה נזהר מהם? מוטיבציה - שיחה 18:05, 22 באוקטובר 2012 (IST)

באף אחד מהחושים. גם קרינה על-סגולה לא ניתן לחוש באף אחד מהחושים, ובכל זאת היא עשויה לגרום לסרטן. גם הרבה טכנולוגיות "ננו" לא ניתן לחוש באף חוש, ובכל זאת יש להם משמעות אדירה לחיינו. זה נראה לי קריטריון לא רלוונטי. לגבי הסכנה, הפשט הוא שאם אתה נוסע לבקר בכור גרעיני, ולא שומר על כללי הבטיחות, אתה עלול להחשף לכמות גדולה של נויטרונים, ולמות (מהר או בייסורים, תלוי בחשיפה). אלקטרונים מהירים ידועים לציבור הרחב בכינוי הידידותי "קרינה רדיואקטיבית" שסכנותיה ידועות. (ישנם סוגים נוספים של קרינה רדיואקטיבית). פרוטונים מהירים לא תפגוש בשום מקום, אלא אם כן ממש תתאמץ להסתכל אל תוך מאיץ חלקיקים בזמן פעולה, מה שיהרוג אותך באופן מיידי. משה פרידמן - שיחה 19:02, 22 באוקטובר 2012 (IST)

לא התכוונתי לומר שזה קריטריון, אלא בסך הכל רציתי לדעת עובדות, האם זה מוחשי או לא, ומדבריך עולה הרושם שלא. יש לי שאלה נוספת בנושא זה הנובעת מתוך בורות כמובן, על איזה בסיס מדעי מונחת תיאוריית החלקיקים? כלומר איך רואים (או איך המדענים יודעים) שבתוך גרעין אטום של יסוד מסויים יש 11 פרוטונים ושמסביב לאטום נמצאים בדיוק 8 אלקטרונים. כמו כך איך יודעים את המרחק היחסי שבין האלקטרון לפרוטון ולניטרון, הרי זו לא מסורת אלא יודעים את זה בעקבות ניסוי כלשהו, ואת הדבר הזה בדיוק אני לא יודע לצערי ומעוניין לדעת. מה שבעיקר מפליא אותי הוא איך ניתן לשקול את החלקיקים הכל כך זעירים האלה שאפילו המיקרוסקופ החזק ביותר לא יכול לראותם על אחת כמה וכמה שלא יהיה ניתן לשקול אותם כביכולמוטיבציה - שיחה 19:47, 22 באוקטובר 2012 (IST)

אתה שואל המון שאלות מצויינות, אבל נראה לי שיהיה קצת קשה להסביר את כל הדברים הללו במסגרת הזו. בכל זאת אנסה. כדי לדעת את כל הדברים הללו צריך לבנות את הפיסיקה שלב אחרי שלב. למשל, כדי לשקול את האטום אנחנו צריכים לדעת את חוקי הפיסיקה הקשורים לחשמל. בעזרתם אפשר לדעת מה הקשר בין מסלול האטום בשדה מגנטי לבין המשקל שלו. אחר כך עושים ניסוי שבו מעבירים את האטום בשדה מגנטי, ומודדים את המסלול שלו, ומתוך כך מסיקים את משקלו. משה פרידמן - שיחה 20:03, 22 באוקטובר 2012 (IST)

אתה מדבר על מסה, מן הסתם, ולא על משקל. בנצי - שיחה 04:05, 23 באוקטובר 2012 (IST)

ניוטרון לא יכול להתקיים לבד לאורך זמן. יש לו זמן מחצית חיים של 15 דקות. פרוטון ואלקטרון מתקיימים לבד. ‏Setreset • שיחה 23:10, 22 באוקטובר 2012 (IST)

ומה קורה איתו לאחר זמן זה, האם הוא הופך לחומר אחר (א"כ, לאיזה)? מוטיבציה - שיחה 18:52, 23 באוקטובר 2012 (IST)

הוא מתפרק לשלושה חלקיקים: פרוטון ועוד אלקטרון ועוד ניוטרינו. ‏Setreset • שיחה 20:21, 23 באוקטובר 2012 (IST)

תודה. מוטיבציה - שיחה 22:36, 25 באוקטובר 2012 (IST)

איזה מחלקיקי האטום הם ממשיים ואיזה מהם לא?

כמו כן, האם האלקטרון הוא ממשי (בדומה לפרוטון למשל), והאם פוטון הוא ממשי? מוטיבציה - שיחה 18:17, 22 באוקטובר 2012 (IST)

לגבי האלקטרון כבר עניתי. הפוטון מאוד ממשי - אדם יכול לראות אותו! משה פרידמן - שיחה 19:22, 22 באוקטובר 2012 (IST)

את הפוטון לא רואים, אלא רואים באמצעות אינטראקציה איתו. ליתר דיוק, תאי החישה ממצים את המידע (השינויים) הגלום באלומת האור או הפוטונים, המייצג את המקור או את העצם ממנו באו. בנצי - שיחה 03:55, 23 באוקטובר 2012 (IST)

אתה מכיר פירוש אחר למושג "ראיה"? משה פרידמן - שיחה 09:10, 23 באוקטובר 2012 (IST)

אין לי ספק שאתה יודע זאת, אבל המשפט שלך לעיל שגוי, ביחוד כשהוא מופנה לְשואל. בנצי - שיחה 10:20, 23 באוקטובר 2012 (IST)

תודה על התשובות. מוטיבציה - שיחה 23:23, 23 באוקטובר 2012 (IST)

את הפרוטון אפשר לטעום. הוא חמוץ. כמעט כל מה שאפשר למשש זה אלקטרונים. אם תעביר הרבה מאוד פוטונים (לייזר) דרך היד שלך, זה יכאב. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אנונימי נכבד, יש לי הרגשה שאתה נמצא ברמה גבוהה בפיזיקה ולכן קשה לי להבין את דבריך. מבחינתי אתה חדת לי חידות. כתבת ש"את הפרוטון אפשר לטעום והוא חמוץ", התוכל להסביר לי את דבריך, כיצד ניתן לטעום דבר כה קטן וכיצד דבר זה הוכח אמפירית?

שנית, כתבת ש"כמעט כל מה שאפשר למשש זה אלקטרונים", שוב גם כאן דבריך לא הובנו לי. והאמן לי שהתאמצתי.

שלישית, כיצד פוטונים קשורים לאלקטרונים? והאם אלקטרונים יכולים לחדור את גוף האדם מצד לצד דרך העצם וכל הרקמות? (אא"כ תאמר שהתחשמלות או חשמל סטטי זו הרגשה של אלקטרונים) בתודה מוטיבציה - שיחה 21:28, 25 באוקטובר 2012 (IST)

האנונימי סתם כתב שטויות. ‏Setreset • שיחה 21:35, 25 באוקטובר 2012 (IST)

דווקא לא. הוא כניראה יודע קצת על מה הוא מדבר, אבל אוהב להתחכם. אפרש אותו: חמיצות נובעת מיונים ולכן קשורה לפרוטונים. העובדה שעצמים (כמו אצבע, שולחן או כפית) לא עוברים אחד דרך השני קשורה לכוח החשמלי שמפעילים האלקטרונים בקצוות שלהם. את ההערה על הפוטונים נראת לי טיפשית (גם אם היא נכונה...). למה לא פשוט להגיד שאפשר להרגיש את חום השמש? ירון ק. - שיחה 22:18, 25 באוקטובר 2012 (IST)

הפרוטון חמוץ בצורה פשוטה ביותר. תשים כמה (הרבה) על הלשון ותרגיש שזה חמוץ. הדבר קורה דרך יוני הידרוניום, H9O4+, ודומיהם. לא היו לי כוונות להתחכם. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אני משער שזה ברור שהתיאור של לשים כמה (הרבה) פרוטונים על הלשון הוא לא מציאותי. אפשר לשים תערובת של פרוטונים עם דברים אחרים, אבל זה לא אותו דבר. ירון ק. - שיחה 08:18, 27 באוקטובר 2012 (IST)

הגדרת כוח ב-CGS

איך ניתן להגדיר את יחידת הכוח במערכת זו על מנת שיהיה אפשר לקיים את השוויון F=ma. בהסתמך על מה שידוע לי ב-SI, על ידי המרת הקילוגרמים לגרמים ומטרים לסנטימרים, פיתחתי ש:

1000[R]=10[g]*1[cm]/[s]^2

כש-R הוא יחידת הכוח...

אפשר לצמצם ולשחק גך ש[R], הוא גרם אחד כפול סנטימטר אחד חלקי 100 שנייה בריבוע. השאלה שלי אם אני יכול להגדיר את הכוח הזה בדומה להגדרה של ניוטון כ"הכוח שצריך להפעיל על מנת סמסה במשקל קילוגרם תנוע מ' במשך שנייה". לדוגמה - הכוח שצריך להפעיל כדי שעשירית גרם תנועה לאורך מילימטר בשנייה. זה נשמע לי מעט קלוקל... אביעד‏ • שיחה 20:27, 22 באוקטובר 2012 (IST)

אם אתה רוצה שיתקיים F=ma, אז בפרט כאשר המסה היא 1 (גרם) והתאוצה היא 1 (סנטימטר לשניה בריבוע), הכוח יהיה שוה ל-1*יחידת הכוח. לכן, יחידת הכוח שאתה רוצה להגדיר היא "כמות הכוח שנדרש כדי להאיץ מסה של גרם בתאוצה של סנטימטר לשניה בריבוע" --84.229.217.206 22:08, 22 באוקטובר 2012 (IST)

זה לא קלוקל. לכל היותר, זהו עניין של נוחות או מקובלות. שים לב לתשובת קודמי - אתה מגדיר מחדש באמצעות גדלי יחידה של מסה ושל תאוצה, שוב, כי כך נוח לקבוע בסיס תקני. באופן זה, או בכל אופן אחר, אתה מקבל את הגדרת היחידה המתאימה של כוח. במקרה הנדון זהו דין. בנצי - שיחה 03:42, 23 באוקטובר 2012 (IST)

פרדוקס הסולם - גרסה 2

הועבר מויקיפדיה:הכה את המומחה

נעשה ניסוי מחשבתי: מעגל חשמלי בעל 2 מתגים, שצריך ללחוץ על 2 כפתורים בו זמנית כך בשביל שהנורה תדלק. כלומר, אם המרחק בין הכפתורים הוא 5 ס"מ והיד שלי היא 5.1 ס"מ אז אני יכול לסגור את המעגל- לשים יד על 2 הכפתורים בו זמנית ואני אראה נורה נדלקת. עכשיו, היד שלי היא 4.9 ס"מ והדרך היחידה לסגור את המעגל היא לרוץ במהירות הקרובה למהירות האור. המרחק בין הכפתורים יתקצר ויהיו כמה רגעים בהם היד שלי תכסה את המעגל והנורה תעבוד.

במערכת המעגל, במעבדה יראו דבר אחר: אני (הניסיונאי שדיבר קודם) רץ ולכן מתקצר. הדבר היחיד שהיד הקצרה יכולה לעשות זה קודם לגעת במפסק הראשון ואחרי זה במספק השני. לכן הנורה לא תדלק כלל. אבל זה סתירה של ממש. זה לא סתם עניין של סימולטניות שבורה כמו "בפרדוקס הסולם" שהציג איינשטיין (האם ניתן להכניס סולם לתוך בית עם 2 דלתות, אתם מכירים). זה עניין של תהליך של כן מתרחש במערכת אחת ולא מתרחש במערכת אחרת. הנורה שיגרה פוטון, המעגל רוקן חלק מהסוללה. ובמערכת המעבדה- כאילו כלום לא קרה. מה אני לא מבין? 79.177.247.15 22:19, 22 באוקטובר 2012 (IST)

זמן

הועבר מויקיפדיה:הכה את המומחה

שאלה חצי פילוסופית חצי מדעית: האם הזמן קיים. אולי הוא בסך הכל פיקציה מתמטית שנועדה לעזור לנו לנתח תהליכים? אני מבין שתפיסת הזמן שלנו מבוססת על הזיכרון, כלומר זו תפיסה שהמקור שלה בכך שאנו יכולים לשחזר בראש תהליך בסדר הגיוני. אבל זו תפיסת אנוש, לא הטבע האבסולוטי. 79.177.247.15 15:21, 23 באוקטובר 2012 (IST)

מה זה "קיים"? עוזי ו. - שיחה 15:33, 23 באוקטובר 2012 (IST)

הוכתי תדהמה. ממשי, ניתן למדידה מספרית, לא יודע להגיד חד משמעית... זה כבר ממש שאלה בפילוסופיה. 79.177.247.15 16:30, 23 באוקטובר 2012 (IST)

"ממשי" לא מוגדר טוב יותר מ"קיים". זמן ניתן למדידה מספרים כמובן, אבל כך גם דברים אחרים שבבירור לא תואמים את מה שאנו מתכוונים אליו ב"קיום". דניאל • תרמו ערך 16:35, 23 באוקטובר 2012 (IST)

מדיד ולא קיים? הדגם. אפר לטעון שזמן לא ניתן למדידה מספרית, אלא כמות מחזורי שעון יד שלך זה מה שאתה מודד. 79.177.247.15 16:40, 23 באוקטובר 2012 (IST)

בחבורת הארבעה של קליין יש 4 איברים, אבל היא לא קיימת בשום מובן פיזיקלי של המילה. למדידת זמן אכן נחוצה יחידת מידה, אבל זה נכון כמעט לכל דבר. גם אורך אנחנו מודדים באמצעות מטר ומסה באמצעות קילוגרם. דניאל • תרמו ערך 19:26, 23 באוקטובר 2012 (IST)

עוזי ודניאל, השאלות שאתם מציגים הן סבבה והכל, אבל אני חושב שאת השואל יעניין יותר לשמוע על ההשערות על הקשר בין חץ הזמן ותרמודינמיקה, נניח. דברים כאלה. --אלעזר - שיחה 21:41, 23 באוקטובר 2012 (IST)

בהחלט. מומלצים הספרים זמן ותודעה (אבשלום אליצור) וזמן ואקראיות (עמית הגר). עוזי ו. - שיחה 01:09, 24 באוקטובר 2012 (IST)

הנושא נידון בהרחבה גם במארג היקום המצוין של בריאן גרין. דניאל • תרמו ערך 10:53, 24 באוקטובר 2012 (IST)

א. אינני יודע מהו 'קיום של זמן', אבל עצם העובדה שתהליכים בטבע דינמיים (תהליכים פיזיקליים, תהליכים כימיים ותהליכים טבעיים אחרים) מעידה על 'קיומו' של הזמן, והוא אינו פיקציה מתימטית או פילוסופית או הכרתית (בדיוק כמו שקיומו של שולחן אינו תלוי בחוש המישוש שלי). יתרה מזאת, לכל סוגי הדינמיקות שציינתי, יש כיוון מוגדר - 'חץ זמן'; לדוגמא, במהלך עונה, אין צמיחה של עלה >> קמילה שלו >> ושוב צמיחה. העקביות הכיוונית הזו היא היא שמקנה לזמן מעמד של משתנה פיזיקלי.

ב. היבט נוסף: לא ניתן למדוד הישתנות של קצב שינוי של משתנה שהוא 'דבר-מה' שאינו קיים. אבל, אפקטים יחסותיים הם דוגמא להישתנות כזו - בקצב השינוי בזמן.

לסיכום, אפשר לייחס לזמן כיוון. ואפשר לייחס לו קצב שינוי. אלו אינם מופשטים פילוסופיים, אלא ישויות ברי-מדידה. בנצי - שיחה 01:40, 24 באוקטובר 2012 (IST)

.

השאלה האם קיים זמן, אינה שונה מהותית מהשאלה האם קיימים אלקטרונים, או האם קיימים שברים, או האם קיימים מספרים בכלל. מה שברור, זה שאנו יודעים: הן שקיימים מרחקים - ארוכים וקצרים, והן שקיימות תנועות - מהירות ואיטיות - שגומאות מרחקים. בשלב הזה, עוד לפני שבכלל הצלחנו לברר האם קיים זמן (ותכף נגיע לזה), כבר אפשר (לפחות) להגדיר את הזמן (שלוקח לתנועה הזו לגמוא את המרחק הזה), בתור היחס (שבין המרחק הזה לבין התנועה הזו). אמנם מתוך עצם ההגדרה הנ"ל - עדין לא נובע אפריורית שקיים זמן, אבל כן נובע ממנה שהזמן (אם הוא בכלל קיים) אמור להיות ארוך יותר - ככל שהמרחק ארוך יותר - וככל שהתנועה איטית יותר, ושהזמן אמור להיות קצר יותר - ככל שהמרחק קצר יותר - וככל שהתנועה מהירה יותר. בשלב הזה מגיעים סוף סוף לשאלתך: האם עצם זה - שהגדרנו כך את הזמן - מצדיק להסיק שקיים זמן; התשובה היא, שאם מניחים הנחה פילוסופית מאד בסיסית, אז כן: ההנחה הפילוסופית הנדרשת כאן - אומרת, שאם קיימים שני דברים (שאף אחד מהם אינו מאופס) אז קיים גם היחס ביניהם; או בנמשל: אם קיים מרחק וקיימת תנועה שגומאת את המרחק הזה, אז - קיים היחס שבין המרחק לבין התנועה - ולכן קיים "זמן" (לפי איך שהגדרנו קודם לכן מה זה "זמן"). לסיכום: קיים זמן (כי קיימים מרחקים וקיימות תנועות שגומאות מרחקים). אמנם, ההוכחה הנ"ל הניחה את ההנחה הפילוסופית הנ"ל, שהיא כשלעצמה אינה הכרחית ואפשר לחלוק עליה (עובדה שיש דברים שאין ביניהם יחס, למשל אין יחס בין אפס לבין אפס). עם זאת, ההנחה הפילוסופית הנ"ל היא מקובלת ביותר (ואף נעשה בה שימוש תדיר - למשל כשמניחים שקבוצה פלונית היא חבורה). אגב, הנחות דומות מאפשרות להסיק ש"קיימים" חלקיקים תת-אטומיים. סמי20 - שיחה 11:38, 24 באוקטובר 2012 (IST)

איפה עובר הגבול בין פיזיקה וכימיה?

כשמדברים על חומר איפה עובר הגבול בין פיזיקה וכימיה? (באחת מהתגובות לאחת משאלותיי כתב אחד המגיבים שמאטום ומטה זהו לא תחום הנוגע לכימיה אלא לפיזיקה), האם זה נכון, והאם זה עונה על השאלה הנ"ל? תודה. מוטיבציה - שיחה 18:47, 23 באוקטובר 2012 (IST)

מקובל שכימיה עוסקת במולקולות ואינטראקציות בינהן ואילו פיזיקה גרעינית עוסקת באטום ומרכיביו. אבל אין פה כללים נוקשים כי זה בסך הכל הענקת שמות, ואפשר שכימאי יעסוק בפיזיקה גרעינית (והרבה פעמים אף יידרש לכך) ולהיפך. דניאל • תרמו ערך 19:19, 23 באוקטובר 2012 (IST)

אכן, זו היתה הערה שלי בדיון קודם, בתגובה לכותרת שאלתך בדיון שאתה מציין. נדמה לי שכבר הישבתי לך שם, אם כי בקצרה. מה לא ברור עדיין ? אשמח אם תחדד את אי הבהירות. עיין גם בשורות הבאות. בנצי - שיחה 01:14, 24 באוקטובר 2012 (IST)

א. זה לא רק עניין של מקובלות ושל הענקת שמות, אלא תוצאה של מכלול תופעות שבשל חשיבותם הרבה לאדם לתחומים שונים, והיותם רווחים כל כך בטבע, נוח להגדיר את הכימיה כדיסציפלינה נפרדת. מכלול זה כולל את תהליכי היווצרותן של מולקולות מאטומים, התפרקותן של מולקולות ושל היווצרותן של מולקולות ממולקולות אחרות. כלומר, תהליכים כימיים רלוונטיים לחלקיקים אטומיים ומעלה. זה מבהיר את ההערה שלי בדיון הקודם שהשואל מזכיר.

ב. יש גם את המרכיב ההיסטורי: שני תחומי הדעת התפתחו בנפרד זמן רב בטרם התברר בהדרגה, הבסיס הפיזיקלי של מדעי הכימיה.

ג. פיזיקה גרעינית לא עוסקת באטום ובמרכיביו, אלא בגרעין האטום ובתהליכים גרעיניים. באטום ובמרכיביו, ובתהליכים ברמה זו, עוסקת פיזיקה אטומית.

ד. כימאי לא עוסק בפיזיקה גרעינית, אלא אם כן בחר לעבור תחום. יותר נכון שתמצא כאלה העוסקים בכימיה גרעינית, כלומר בתחום החוקר את השפעת קיומם של איזוטופים שונים על קצבי תהליכים כימיים, ועוד. ויש כמובן כימיה פיזיקלית, ויש פיזיקה כימית (לפעמים שמות תת-התחומים הם עניין של מקום-אוניברסיטה, או של השפעתו של מדען דומיננטי, ולאו דווקא של מהות), ובסה"כ ישנם שטחי חפיפה בין פיזיקה וכימיה, ובין תת-תחומים שלהם. מה שמעניין הוא שמה שאנו מגדירים ככימיה, בהמשך למה שכתבתי ב(א), מהווה את הבסיס למדעי החיים, ומכאן התפתחו תחומי ביניים, דוגמת ביוכימיה, ותת-תחומים, דוגמת גנטיקה מולקולרית, ועוד.

ה. לסיכום, כל התהליכים הכימיים, שהם ביסודם תהליכי קישור ותהליכי התפרקות, מבוססים על חוקים פיסיקליים, ולכן, מבחינה זו, בהרבה מקרים מחקר מעמיק ויסודי בכימיה, הוא בעצם עיסוק בפיזיקה, והדוגמאות לכך רבות. הסיבה לכך היא שתופעות כימיות נובעות מאינטראקציות אלקטרוסטטיות וטיפול של מכניקת הקוונטים באינטראקציות אלה ובתיאורן. תופעות רבות לא ניתנות להסבר קלאסי, אלא קוונטי, דוגמת השוני בין קשר קוולנטי לבין קשר יוני ולבין קשר מימן, שהן שלוש דוגמאות לקשרים נפוצים מאוד בעולם הטבע. אני מקווה שה'קו' מתוח עתה בצורה ברורה יותר. שאלה מצויינת, והעובדה שהיא חוזרת במובן מסויים, מעידה על התעניינות עקבית. בנצי - שיחה 01:14, 24 באוקטובר 2012 (IST)

נהוג להפריד בין התחומים באזור החפיפה ביניהם, לפי סקאלות האנרגיה הרלוונטיות. תהליכים באטומים ומולקולות שנקראים "פיזיקליים" ולא "כימיים" מאופיינים באנרגיות גבוהות בהרבה. אני מעריך שהגבול עובר בכמה אלקטרון-וולט. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

יחסות פרטית, חישוב

השאלה שלי כאן. אני בסעיף 3. עשיתי ככה:

נעבוד במערכת המעבדה. האנרגיה הדרושה להאיץ את החללית היא $E_{k}={\frac {Mc^{2}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$. האשר M זה ה700 שנתנו, מסת החללית.

עכשיו, הקטע שלא ברור. אני מסמן m מסת הדלק. האם אני צריך לעשות $E_{k}=E_{m}$, כלומר ${\frac {Mc^{2}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}=mc^{2}$, כאילו שהדלק "נמצא במעבדה"? אני יודע שהשאלה עצמה מוזרה בכך שמניחה שהדלק לא חלק מהחללית. אם אני מניח שהוא נע במהירות של החללית אני מקבל ${\frac {Mc^{2}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}={\frac {mc^{2}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$. כלומר משהו מוזר: בשביל להאיץ קילוגרם אחד לכל מהירות שהיא, צריך קילוגרם דלק אחד, בלי תלות במהירות. משהוא פה לא בסדר.

ומה הרעיון בשאלה 4? אני פשוט לא מבין מה זה יכול להיות. 79.177.247.15 18:54, 23 באוקטובר 2012 (IST)

מחפש שם של חוק פיזיקלי או כימי

אני חושב ששמעתי פעם שישנו חוק כלשהו בפיזיקה או בכימיה האומר כי חומר לא נעלם ולא נוצר יש מאין, איך קוראים לחוק זה? (גם כדי שאוכל לקרוא עליו בויקיפדיה). מוטיבציה - שיחה 18:54, 23 באוקטובר 2012 (IST)

חוק שימור החומר. עוזי ו. - שיחה 19:10, 23 באוקטובר 2012 (IST)

כן לזה התכוונתי. תודה. (אגב, הערך הזה עתה קצרמר - השוו עם אנגלית). מוטיבציה - שיחה 23:24, 23 באוקטובר 2012 (IST)

א. או בניסוח נכון יותר: חוק שימור המסה.

ב. אבל, זה לא לגמרי נכון, אלא בתנאים מוגדרים. החוק הכללי יותר הוא חוק שימור המסה-אנרגיה. ישנם תהליכים רבים בהם מסה הופכת לאנרגיה, ולהיפך; וישנם גם שיקולים יחסותיים. בנצי - שיחה 23:39, 23 באוקטובר 2012 (IST)

תודה למשיבים. מוטיבציה - שיחה 21:04, 25 באוקטובר 2012 (IST)

חישוב מרחק המולוקולות במים

כיצד ניתן לחשב את המרחק הממוצע בין מולוקולות מים סמוכות? אביעד‏ • שיחה 20:15, 23 באוקטובר 2012 (IST)

מול אחד של מים שוקל כ-18 גרם ולכן נפחו כ-18 סמ״ק. זה אמור להספיק כדי לחשב את המרחק בין המולקולות (אפשר להניח שהן מסודרות בסריג). Easy n - שיחה 20:41, 23 באוקטובר 2012 (IST)

א. לא שוקל 18 גר', אלא מסתו 18 גר'. זה נכון גם מבחינת היחידות, וגם מבחינת העובדה שהמשקל משתנה ממקום למקום.

ב. הנתונים שאתה מספק מתייחסים כמובן לתנאי טמפ' ולחץ תקניים, כלומר, לטמפ' החדר (27⁰C), וללחץ אטמוספרי (בגובה פני הים).

ג. הם לא תמיד מסודרות בסריג, וגם בצורת מוצק לא תמיד זה כך, בודאי לא קובי. הסיבה לכך סוג הקשר בין המולקולות - קשרי המימן בין אטומי חמצן לאטומי מימן במולקולות סמוכות. אבל למציאת המרחק הממוצע אכן די בחישוב מס' מולקולות ליחידת נפח. בנצי - שיחה 00:01, 24 באוקטובר 2012 (IST)

מותר להניח שהמים מסודרים בקובייה, כדי להקל על החישוב? אביעד‏ • שיחה 06:59, 24 באוקטובר 2012 (IST)

במציאות לא, משום שהקשרים הבינמולקולריים לא מאפשרים למולקולות המים ליצור סריג קובי (כלומר, כזה שהמולקולות ממוקמות בקודקודי הקוביה). אבל החישוב האמור הוא בכל זאת נכון, משום שהוא מבוסס על גישה אחרת: כמה מולקולות יש לי בנפח נתון, מה שמאפשר לקבל מרחק הדדי ממוצע - כאילו מדובר בסריג קובי. בנצי - שיחה 09:54, 24 באוקטובר 2012 (IST)

אתה קטנוני. בשביל לחשב מרחק ממוצע (שזה מה שביקש השואל) ניתן להניח סידור בסריג. מכיוון שהשואל לא ציין נתוני לחץ וטמפרטורה, ניתן להניח שהם סטנדרטיים, מה גם שסדר הגודל לא ממש משתנה כשמדובר במים נוזלים. Easy n - שיחה 10:46, 24 באוקטובר 2012 (IST)

א. אתה לא נמצא במקום ממנו אתה יכול לדבר על "קטנוניות". אין מקום למושגים שגויים או לנתונים חסרים (גם אם, לדבריך, ניתן להניח שהם תקניים, עדיין יש צורך לציין את התלות הזו).

ב. לא ניתן להניח סריג קובי פשוט, כי הם לא. לא מספקים תובנות שגויות כדי לקבל תוצאה. עם זאת, את המרחק הממוצע אפשר לקבל כאילו מדובר בסריג קובי וירטואלי כזה. צריך לציין את ההבדל הזה, ואת בסיס ההנחה, ולא להסתפק בהנחה סתמית.

ג. מותר לשגות, אבל לא להפוך אותן אוטומטית ל"קטנוניות". בנצי - שיחה 11:30, 24 באוקטובר 2012 (IST)

אתם מתעלמים מהעובדה שהשואל לא הגדיר למה הוא התכוון בדיוק ב"מרחק ממוצע". אני יכול לחשוב על יותר מהגדרה הגיונית אחת. דניאל • תרמו ערך 10:52, 24 באוקטובר 2012 (IST)

לא מדובר בממוצע בזמן, אם לזה אולי התכוונת. 'מרחק ממוצע' מתקבל בהסתמך על יחידת הנפח אותה תופסת כל מולקולה בתנאים מוגדרים, וכפי שהסברתי קודם. בנצי - שיחה 11:33, 24 באוקטובר 2012 (IST)

מה בדיוק ההגדרה? דניאל • תרמו ערך 11:49, 24 באוקטובר 2012 (IST)

התבונן למשל, באיור השני בקרח. המבט שם הוא כמעט מבט-על, אבל מראה היטב את סידור מולקולות המים במרחב, הנובע מקשרי המימן ביניהן, ואת העובדה שאין סימטריה ברמה של המולקולה הבודדת. מכאן הצורך בהגדרה האמורה של מרחק ממוצע: שורש שלישי של הנפח למולקולה אחת, המבוסס על הנפח הכולל מחולק במס' המולקולות (מס' המולקולות במול אחד של מים הוא מס' אבוגדרו). בנצי - שיחה 16:14, 24 באוקטובר 2012 (IST)

המספר שמקבלים מהחישוב שנתת לא מתאר את מה שנקרא אינטואיטיבית המרחק הממוצע (במבנה שאינו סריג קובי). דניאל • תרמו ערך 22:38, 24 באוקטובר 2012 (IST)

פיתרון מד"ר

איך פותרים (בלי ניחוש) את המד"ר $y''(x)+ay(x)=0$ כאשר a קבוע. בשיטת הניחוש זה יוצא ממש קל (פונקציה ידועה). אבל אני רוצה פתרון "שלם". עשיתי קורס מד"ר לפני יותר משנה. 79.182.199.116 20:00, 24 באוקטובר 2012 (IST)

ראה en:Cauchy–Euler equation. דניאל • תרמו ערך 22:42, 24 באוקטובר 2012 (IST)

סמל האליפסות בפיזיקה - מהו?

בפורטל הפיזיקה בויקיפדיה למשל, יש סמל כזה של מספר אליפסות מחוברות מכיוונית שונים, מה מהות הסמל הזה? האם זה מסמל אם הפרוטון ואת הנייטרון ואת האלקטרונים שחגים סביבם בצורת אליפטית? (ניסיתי לחפש מידע בערך פיזיקה ולא מצאתי). ראיתי הרבה סוגים של הסמל הזה, והמסקנה העולה היא שאין סמל אחיד אלא רק הכיוון של האליפטיות. אשמח להסבר על הנושא הזה. תודה. מוטיבציה - שיחה 20:50, 25 באוקטובר 2012 (IST)

זהו ציור המתאר הבנה ישנה של מבנה האטום. הציור הזה התקבל בציבור הרחב (וגם בקהילה המדעית), כמין סמל כללי לפיסיקה בכלל, ולפיסיקה האטומית בפרט. למרות שהוא איננו מדוייק, הוא מאוד פשוט לציור, נוח למתבונן, ונותן אינטואיציה כללית למבנה האטום. בציור הזה מתואר האטום גרעין המונח במרכז, וסביבו חגים במסלולים אליפטיים אלקטרונים. משה פרידמן - שיחה 21:20, 25 באוקטובר 2012 (IST)

אז במילים אחרות ציור זה מציג תיאוריה שהייתה ואיננה עוד, תיאוריה שלא רלוונטית לזמננו. יש דגם יותר מתקדם שמייצג את התיאוריה העכשווית או שדגם זה בבחינת שיבוש שנשתרש (בדומה ל'חמצן') ואין דגם מחליף למרות שהתשתית הוחלפה? אגב, בהזדמנות זו אפשר בבקשה לדעת במה שונה התיאוריה שהוא מייצג מהתאוריה של זמננו- ולו 'על קצה המזלג'? ובכלל האם יש לסמל זה שם בעברית? (באנגלית אני חושב שהוא נקרא atom symbol). מוטיבציה - שיחה 21:59, 25 באוקטובר 2012 (IST)

ראה: המודל הפלנטרי. שמוליק - שיחה 22:08, 25 באוקטובר 2012 (IST)

המודל הפלנטרי הוא מודל ישן, והוא מציין את אחד השלבים המשמעותיים הראשונים בהבנת מבנה האטום. בנצי - שיחה 02:44, 26 באוקטובר 2012 (IST)

א. כפי שהסבירו לך קודם, זהו סמל בלבד, הנותן מושג כללי ביותר לגבי מבנה האטום. ליתר דיוק, הוא ממחיש בצורה היוריסטית את העובדה שהאלקטרונים 'חגים' מסביב לגרעין במסלולים אפשריים שונים בדידים, ולא כמו במודל תומסון; שתי עובדות אלה הן נכונות, במגבלות הסמל כמובן, והצורך בעיצוב פשוט ככל האפשר.

ב. אגב, לדעתי, המסלולים בסמל אינם בדיוק אליפטיים, אלא מבט פרספקטיבי (מבט מהצד) על מסלולים מעגליים.

ג. שאלת על הבדלים: 1. התמונה המתקדמת יותר אינה מדברת על מסלולים מישוריים, כפי שניתן להתרשם בסמל (בדומה למודל הפלנטרי), אלא על משטחים מרחביים המציינים הסתברות מירבית למצוא אלקטרון במצב קוונטי נתון (מצב קוונטי מאופיין ע"י 4 מספרים קוונטיים). מצבים קוונטיים יסודיים אכן מתוארים ע"י משטחים כדוריים מתאימים. 2. הסמל אינו יכול לתאר את הפרופורציות של מימדי האטום כולו (למשל משטח ההסתברות של האלקטרון החיצוני ביותר) לעומת מימדי הגרעין. הסיבה לכך היא מימדי הגרעין שהינם זעירים ביותר; לשם השוואה, היחס ביניהם הוא בסדר הגודל של מימדי כדור (בהנחה שמדובר במשטח כדורי) שקוטרו הוא כאורכו של מגרש כדורגל, לעומת קוטרה של גולה. בנצי - שיחה 02:44, 26 באוקטובר 2012 (IST)

על קצה המזלג: מסתבר שהאלקטרון אינו "גולה קטנה" שמסתובבת אלה משהוא מרוח במרחב ללא מיקום (או מהירות) מוגדרים. אתה אולי יכול לתאר לעצמך שהרבה יותר קשה לצייר מודל כזה. (דרך אגב סמלים ציוריים מיושנים זה דבר די נפוץ: לדוגמה הסמליל של שמירת קובץ) ירון ק. - שיחה 10:45, 26 באוקטובר 2012 (IST)

הגולה התייחסה למימדיו היחסיים של הגרעין. בנצי - שיחה 19:15, 26 באוקטובר 2012 (IST)

מה ההבדל בין ציון תקן לסטיית תקן?

האם אפשר לקבל הסבר בשפה פשוטה מה ההבדל בין ציון תקן לסטיית תקן (אם אפשר עם המחשה קטנה - זה יותר טוב). קראתי את הערכים הרלוונטייים בויקיפדיה. כמו כן, מה מסמלת האות S של סטיית התקן (האות היא קיצור של מילה כלשהיא) ומה מסמלת האות Z של ציון התקן (האות היא קיצור של מילה כלשהיא). מוטיבציה - שיחה 22:55, 25 באוקטובר 2012 (IST)

נתון מדגם של n מספרים, x1,x2,...,xn. למדגם יש ממוצע ${\bar {x}}={\frac {1}{n}}(x_{1}+\cdots +x_{n})$ (מספר שנתוני המדגם קרובים אליו ביותר, במובן מסויים) וסטיית תקן $\,s={\sqrt {{\frac {x_{1}^{2}+\cdots +x_{n}^{2}}{n}}-{\bar {x}}^{2}}}$ (המרחק של נתוני המדגם מן הממוצע: ככל שסטיית התקן קטנה יותר הנתונים מרוכזים יותר). את סטיית התקן מקובל לסמן ב-s שהיא האות הראשונה של המלים Standard deviation (אפשר היה לקרוא לזה "סטיה מן התקן"). ציון התקן של ערך x (יכול להיות אחד מנתוני המדגם, או ערך חדש) הוא המספר ${\frac {x-{\bar {x}}}{s}}$ שמודד את המרחק של x מהממוצע ביחידות של סטיית התקן. את ציון התקן מקובל לסמן ב-z, ככל הידוע לי ללא שום סיבה מיוחדת. ההבדל העיקרי בין ציון התקן לסטיית התקן הוא פיזיקלי: סטיית התקן, כמו הממוצע, נמדדת באותן יחידות שבהן נמדדים נתוני המדגם (מטרים, שקלים חדשים לדקה בריבוע, וכו'). ציון התקן הוא סקלר חסר יחידות. עוזי ו. - שיחה 00:30, 26 באוקטובר 2012 (IST)

השאלה היא מה הוא התקן עצמו? (כדי שאוכל להבין את מהות הסטיה). אין לי בעיה לפתור בעיות עם סטיית תקן, אבל אני עושה את זה כמו רובוט ולא מבין את המשמעות. כמו כן, האם יכול להיות שהאות S מתכוונת גם למילה swerve (סטייה)? 109.253.2.189 12:41, 26 באוקטובר 2012 (IST)

ה"תקן" הוא להיות שווה לממוצע. בכל התפלגות שפויה בדעתה יש סטיות מן הממוצע, וסטיית התקן מודדת את גודל הסטיות האלה. עוזי ו. - שיחה 13:41, 26 באוקטובר 2012 (IST)

תודה. אז אם אני מבין נכון התקן הוא הוא הממוצע. או במילים אחרות סטיית תקן= סטיית ממוצע. מוטיבציה - שיחה 22:30, 27 באוקטובר 2012 (IST)

כוכבים נצפים

הועבר מויקיפדיה:הכה את המומחה

האם נכונה הטענה, שהכוכבים שאנו רואים מכדור הארץ, כולם משתייכים לגלקסיית שביל החלב, לא לגלקסיות אחרות מרוחקות יותר ? במידה וכן, האם הדבר אמור אך ורק בצפייה בעין בלתי מזוינת כמסתבר ? טיפוסי - שו"ת 01:56, 26 באוקטובר 2012 (IST)

העצמים שנראים בשמי הלילה מתחלקים לכמה סוגים. האחד הוא כוכבי הלכת הקרובים לנו. השני הוא עצמים קרובים אלינו יחסית בתוך שביל החלב. בעיקר מערכות של כמה כוכבים (שנדמים לנו בעין לא מזוינת ככוב אחד), למשל כוכבים כפולים. השלישי הוא מבנים גדולים מאוד מחוץ לשביל החלב. למשל ענני מגלן וגלקסיית אנדרומדה. באמצעות טלסקופ חזק ניתן לבחון את המבנה הפנימי של גלקסיות אחרות רבות. דניאל • תרמו ערך 02:50, 26 באוקטובר 2012 (IST)

קוטר שביל החלב הוא 100,000 שנות אור, וכמעט כל הכוכבים שאפשר לראות בעין בלתי מזויינת כבודדים הם במרחק של כמה עשרות או מאות שנות אור, כלומר, ממש מעבר לפינה. אפשר לראות כוכבים בודדים בגלקסיות רחוקות רק בנסיבות יוצאות דופן, כמו למשל כשהם נעשים סופר נובה. עוזי ו. - שיחה 02:52, 26 באוקטובר 2012 (IST)

תודה. ביקום אדיר ובלתי נתפס זה שאנו עוסקים בו, רב הנסתר על הגלוי. מה רבו מעשיך השם. טיפוסי - שו"ת 03:08, 26 באוקטובר 2012 (IST)

הדבר הכי לא נתפס בו זה למרות שיש עדויות ברורות לכך שהיקום בן ביליוני שנים, עדיין יש אנשים שחושבים שהוא נברא לפני איזה 5-6 אלף שנה. ורובם גם מסרבים לשמוע על כך שמהירות האור היא גודל סופי ולכן אם מרחק ביננו לבין כוכב כלשהו הוא 6 ביליון שנות אור, אז לא יתכן שנראה אותו אלא אם כן חלפו 6 ביליון שנה. 109.65.243.209 19:34, 27 באוקטובר 2012 (IST)

שלום לך. לא הספקתי להגיב לדבריך קודם, ורק אומר שדבריך מאוד במקומם, נכונים וחשובים. תבורך. בנצי - שיחה 09:25, 29 באוקטובר 2012 (IST)

העדויות הברורות שאתה מדבר עליהן, הן לא אחר מאשר השערות והנחות בלתי מבוססות שמעולם לא אומתו, וכשמשוים אותן לסיפור הבריאה התנכ"י הן באמת שוות כקליפת השום, בעיני היהודי המאמין כמובן. טיפוסי - שו"ת 00:16, 29 באוקטובר 2012 (IST)

א. אני מבקש ממך להפסיק לדקלם את הרעיונות הללו. הסוגיות הנדונות דורשות ידע יסודי הנרכש בעמל רב של למידה, התמסרות והתמדה. האם אתה בא משם ? אין מדובר בהשערות, כי חוקים פיזיקליים אינם פיקציה - זה רציני מאוד. בלעדיהם קיומך לא היה אפשרי כמערכת, וכך גם כל תא ותא בגופך. אנא חדול מכך. זה אינו ויכוח, ולא מדובר ב'דעות'. כדי להבין את קצה קצה של בעיה מדעית ולהיות מסוגל לטעון דבר מה בקשר לכך, נדרש, לפחות, להשיג ידע והבנה מובנים ומסודרים. לא היית מעיז להתערב בויכוח בין מהנדסים הבונים גשר, או בין רופאים הדנים בחולה או מחלה. אבל כאן אתה מרשה לעצמך, משום שאינך נושא באחריות או מחוייב בתוצאות של דבריך. 'לופטגשפט' - מכיר ??

ב. בפרט, נא מחק את הביטוי "הן באמת שוות כקליפת השום". זהו ביטוי מזלזל קיצוני, המציב אוטומטית, אמונה לא מוכחת עפ"נ תובנות המבוססות היטב מכל בחינה שהיא. כל העולם המדעי בצד אחד, ורק טיפוסי מעמיד את עצמו בצד השני, וסבור אחרת מהם. קצת צניעות !!

ג. אין לך מונופול על יהדות מאמינה, והפסק לדבר בשמם; לכל היותר דבר בשם עצמך ובשם אנשים המחזיקים בדעות כשלך. בצד יהודים מאמינים הסבורים כמוך (גם נוצרים מאמינים אגב, וגם מוסלמים מאמינים), ישנם יהודים מאמינים שאינם מקבלים זאת כלל ועיקר. אזכיר שוב את הרמב"ם. ידועה לי כבר 'הפרשנות' שלך לגבי כוונתו, ואין צורך לחזור עליה. שוב, יהודים מאמינים רבים, שהם תלמידי חכמים וגם חוקרים אקדמיים בתחום, סבורים אחרת ממך. את חלקם אני מכיר באופן אישי. כבד אותם. גם על זה אין לך מונופול.

ד. כפי שכבר כתבתי בעבר: אין שום ערך לטענות בעלות אופי מדעי, מבלי שהן מבוססות. אין די בדקלום מילולי והצהרתי המבוסס על אמונה. בנצי - שיחה 09:25, 29 באוקטובר 2012 (IST)

בנצי, אני מבין שאצלך המדע זה חזות הכל, זה לא נורא, אבל זה בוודאי לא מוכח. קל וחומר שזה לא מצדיק את ההשתלחות חסרת הרסן וההגיון שלך כלפי טיפוסי. החוקים הפיסיקליים עשויים להיות פיקציה, על אף שהם רציניים מאוד. להגיד שבלעדיהם קיומו לא היה אפשרי זו כבר שטות מוחלטת, המצביעה על כך שכלל לא ניסית להבין את טענת הצד השני - וחבל שכך. לכנות את תובנות המדע כ"מבוססות היטב מכל בחינה שהיא" זו כבר ממש בורות בפילוסופיה של המדע. הקהילה, שאני גאה להיות חלק ממנה, בחרה להיפטר במודע ממספר שאלות עקרוניות העומדות בבסיס על מנת לייצור התקדמות. זו בעיני בחירה ראויה. אבל להסיק מכך משהו על מהותן של אותן שאלות זו הזיה. משה פרידמן - שיחה 09:52, 29 באוקטובר 2012 (IST)

א. לא אגיב לדבריך, משום שאינם ענייניים, ובעיקר, מתנשאים ופוגעים. אתה לא מדבר איתי, אלא שופט את דבריי ומבטל אותם תוך שימוש בכינויים פוגעניים. גם בנסותי לדוג איזשהו עקרון חשוב בדבריך שאולי פיספסתי, אינני מצליח. אתה מכליל, ואין בדבריך דיון לגופן של סוגיות. דיון כזה היה מרחיב דעת, והיה מחדד את הגישה המתודולגית בה אני דוגל, ואת גישתך שלך. לי זה חבל, אבל לא אטול חלק בשיח פוגעני ו'מחלק ציונים'.

ב. אני מבקש ממך להסיר את הביטויים: בדבר "השתלחות חסרת רסן", "שטות מוחלטת", "ממש בורות" ו"הזיה". לא רק אתה נמנה על אותה קהילה, ואמנע מלמנות שורה ארוכה של מדענים וחוקרים, שאינם סוברים בדיוק כמוך או לפי גישתך. אסתפק ביובל נאמן, כנציג ישראלי, ובמארי גל-מאן כנציג אמריקני. לידיעתך, התייחסות לביטויים פוגעים אלה שלך תופנה לאן שצריך.

ג. הייתי שמח אילו יכולתי להרחיב את הדיון איתך ולהעמיק אותו, לגבי ההיבטים העולים הן מדבריי לעיל, והן מדבריך. אינני חושב שאתה מבין את הבעיה עליה אני מדבר. אתה גם לא טורח לברר זאת. כך היה גם בעבר. כך גם בהווה. שוב, לא אנהל איתך דיון, בעיקר כאמור, בשל הביטויים הבוטים והפוגעים.

ד. לא ראיתי בדבריך התייחסות לביטוי "לא שווים כקליפת השום" שלו לעיל. מעבר לדיון גופו, זהו ביטוי לא ראוי, גם לפי אמות המידה של דבריך שלך. בנצי - שיחה 10:26, 29 באוקטובר 2012 (IST)

אדרבה, אני מעוניין שתפנה אותם לאן שצריך. זאת משום שבתגובתי הקודמת ניסתי לשקף בפניך את היחס השופט המזלזל והמתנשא שלך, באופן עקבי, כלפי אחרים. מכיוון שהצהרת שאינך מתכוון להגיב לדברי, אין כל הגיון בכך שאמשיך לטעון לגופם של דברים. גם אין כל צורך לבקר את הביטוי של טיפוסי, משום שהוא גם לא ביטוי שיפוטי כלפי הזולת, וגם מדוייק לחלוטין. משה פרידמן - שיחה 11:47, 29 באוקטובר 2012 (IST)

א. אתה ממשיך לפגוע. אתה מכליל, ולא מכבד אותי במידה מספקת, כדי להבהיר את השיפוט הקיצוני שלך כלפיי באמצעות דוגמאות שיש בהן כדי לתמוך בטענה שלך, ולא נותן לי 'צ'אנס' לבדוק על מה בדיוק מבוססות טענותיך או הרגשתך. זו ההגדרה הקלאסית של שיפוטיות והתנשאות. אתה גם נוקט בהכללות והכפשות, משל הדבר היה לגיטימי ו'מטבע עובר לסוחר', כולל האשמתי לכאורה, "בזלזול ובהתנשאות עקביים". אני חש שהתנהלותך כלפיי, ולא מהיום, היא אישית ואנטגוניסטית לחלוטין, ביחוד, כאמור, כשהיא נטולת כל היגד ענייני המאפשר בחינה מעמיקה של טיעון כזה או אחר, הן במישור המדעי והן במישור טענותיך. מה אתה רוצה ? דעתי שונה לחלוטין משלך, למרות שאנו משתייכים לאותו מילייה. מדוע אינך מכבד זאת ?

ב. ניסיתי לרמוז לך קודם שהשיח עם טיפוסי הוא מסוג והקשר שונים לגמרי מהויכוח איתך. אבל אתה מתעקש להתעלם מכך. מניעיו אמוניים ולא ענייניים, בניגוד לך, או שאני טועה לגבי מניעיך. בנצי - שיחה 12:27, 29 באוקטובר 2012 (IST)

א. בנצי, כמו שכתבתי למעלה, אני מנסה לשקף לך את ההתנהלות שלך. נסה לחשוב רגע כיצד חש טיפוסי כאשר הוא קרא את ההודעה שלך למעלה, ותבין מה גרם לי לנסח את הודעתי כפי שניסחתי. אני טוען שהדבר הוא עקבי, משום שפעמים רבות אתה מגיב לאנשים במסגרת זו בצורה שיפוטית ואף מחנכת, באופן שאתה לא היית מקבל בהבנה אם הייתה מופנית כלפיך. בדרך כלל אני מתאפק ולא מגיב לדברים, משום שאני לא חושב שיש סיכוי לשנות את היחס הזה שלך, אבל לפעמים כן.

ב. איזה טעם יהיה בלנסות להגיב עניינית, כאשר אתה מצהיר מראש שאינך מעוניין להגיב לדברי?

ג. בהודעה המקורית שלי, שנכתבה, כאמור, בניסוח המבקש לשקף בפניך את היחס שלך כלפי טיפוסי, הגבתי בצורה עניינית לחלוטין, אם כי בקיצור נמרץ.

ד. אני מאוד מכבד דעות שונות משלי. אני רק מנסה להציג בפניך שגם עמדתו של טיפוסי (שאיננה זהה לדעתי) היא לגיטימית, ולא ראויה להתייחסות המבזה לה היא זכתה בהודעה שלך מלמעלה. משה פרידמן - שיחה 13:15, 29 באוקטובר 2012 (IST)

אתייחס ל-(ב) לעת עתה, ורק לזה, משום שממנו נובע חוסר רצוני להגיב: דבריך שם מניפולטיביים, כי הם מובאים בצורה מסולפת ונטולת הקשר - אתה בוחר את הפרשנות שנוחה לך. לא הצהרתי "שאיני מעוניין להגיב". הצהרתי משהו אחר לגמרי: אינני מעוניין להשתתף בדיון בו משמיעים הכפשות אישיות, וכינויים, שיפוטיים ואחרים, נוטלים בו חלק. אני מקווה שעתה נקודה זו ברורה לך. לא אטול חלק בשיח מן הסוג הזה, ויש לי זכות מלאה להימנע מכך. בנצי - שיחה 14:18, 29 באוקטובר 2012 (IST)

בנצי, שאלה ידידותית, האם ואולי תנסה להפנים את הביקורת המנומקת שמשה מפנה כלפיך? ואגב, אני סבור שאדם שאינו מסוגל לכבד קיומן של השקפות עולם מנוגדות לשלו, תהיה זו ציפיה מוגזמת מצידו לכך שהשקפת העולם שלו תזכה ליחס אוהד יותר מצד המתנגדים לה. בברכה. טיפוסי - שו"ת 14:33, 29 באוקטובר 2012 (IST)

(הוספה לאחר התנגשות עריכה) כלומר, אתה מוכן להשתתף בדיון מבלי לזלזל מראש בדסיפלינות שונות משלך, מבלי לכנות עמדות של אחרים "דקלומים", מבלי לרמוז שהצד שכנגדך חסר את הידע הבסיסי על מנת להשתתף בדיון, ומבלי לטעון כנגד יריבך שעמדתו לוקה בחוסר צניעות? כי אז אומר, שהשיטה המדעית לוקחת כאקסיומות מספר הנחות בסיסיות העומדות בסתירה מוחלטת לאמונתו של טיפוסי. הרי הנחתו של טיפוסי שהעולם נברא באופן שאיננו מציית לאף חוק טבעי אלא כביטוי לרצון האל, עומדת בסתירה מהותית לכל יסוד המאפשר עבודה מדעית. מובן מאליו, איפה, שכל ראיה מדעית, המבוססת על עקרונות המדע, לא תוכל להעלות או להוריד במאומה את תקופתה של ההנחה היסודית, שהטבע מציית לוחקים נוקשים ולא לרצונותיו של האל. לכן צדק טיפוסי כשאמר, שעבוד המאמין כל ההוכחות הללו שוות כקליפת השום, ואין בכך שמץ של חוסר צניעות. (רק באמת אני מצר על כך שכלל איתו את כל היהודים המאמינים). שכן מה תועיל לו למדען תצפית אל כוכב במרחק מליון שנות אור, אם טיפוסי יטען כנגדו שלפני 20 דקות האל ברא את הכוכב, ועשה לקרינה שלו "קפיצת הדרך" היישר לעבר הטלסקופ שלך? מה תועיל לך הטענה שתהליכים גיאולוגים לוקחים כך וכך שנים, אם טיפוסי יטען כנגדך שהעולם נברא מראש כעולם מפותח, הנראה זקן לעיננינו בלבד? היוצא מדברינו, שהוויכוח בין עמדתו הדתית של טיפוסי לבין העמדה המקובלת בזמננו היא ברמת האקסיומות, ועל כן כל העבודה המדעית הענפה והמכובדת לא תוכל להציב את מאמיניה בעמדה עדיפה בוויכוח שכזה. אמת, שגם בעיני אין כל צורך לטעון טענות משונות שכאלו כדי להגן על הבנה לא הכרחית של הכתובים, אבל אין כל מקום להתנשאות של אנשי המדע על מאמינים מסוגו של טיפוסי בטענות שהידע שלהם במדעים חסר. פעמים רבות (אם כי לא בהכרח) זוהי טענה שאיננה מן העניין. משה פרידמן - שיחה 15:03, 29 באוקטובר 2012 (IST)

סחטיין על האידאליזציה. אבל ברוב המוחלט של המקרים הגישה הדתית באמת נובעת מחוסר ידע, כלומר אמונה מבוססת על בורות. 192.114.105.254 15:19, 29 באוקטובר 2012 (IST)

האמת, לדעתי, שברוב המקרים הגישה של הדתי, כמו כל גישה אחרת, מבוססת על הרקע האישי המשפחתי והלאומי של אותו הפרט. זה נכון באותה מידה גם לגבי החילוני, ואפילו לגבי המדען החילוני. זה נכון, לצערי, שבחברה החרדית קיימת בורות עצומה ולעיתים אך עוינות לא מוצדקת כלפי השיטה המדעית. יחד עם זאת, אל תשלה את עצמך שאי-דתיותו של החילוני הממוצע מבוססת על הכרות מעמיקה עם שתי הדסיפלינות והכרעה באחת מהן. בדרך כלל מדובר על בורות בפילוספיה של המדע ובמדע עצמו, ובורות עמוקה מכך בתפיסה הדתית משה פרידמן - שיחה 15:26, 29 באוקטובר 2012 (IST)

משתמש:192.114.105.254 ניתן להשכיל מדברי משה שלמקל יש שני קצוות, ולמטבע שני צדדים. טיפוסי - שו"ת 16:35, 29 באוקטובר 2012 (IST)

בעזרת טלסקופים (לא חובבניים, אלא טלסקופים גדולים כמו שאדווין האבל השתמש בהם) אפשר בהחלט לראות כוכבים בודדים גם בגלקסיות קרובות. ככה מצאו את המרחק אליהן (כשהסתכלו על משתנים קפאידים). eman • שיחה • ♥ 10:23, 26 באוקטובר 2012 (IST)

משה ובנצי, תודה רבה ויישר כוח לשניכם. טיפוסי - שו"ת 11:57, 29 באוקטובר 2012 (IST)

בנצי היקר, אי אשפר לטעון שבימנו בורות היא עניין של בחירה. את נוזף באדם בוגר על כך שאינו מוכן לקבל עובדות מדעיות אלא מעדיף לספר על כישופים, עין הרע ובחישה בכוס עופרת. הזלזול במדע במקרה הנ"ל אינו נובע רק מבורות, אלא מהתייחסות למדע כ"דת אחרת". וכמו בדת מתייחסים למדענים ככוהני דת ולא כחוקרים. התעקשות באמונה זו והבורות שאמונות אלו מביאות אינן פרי בחירה, אלא באים מרקע מסוים. הרקע הסוציאו-תרבותי ולימודים בקו מסוים מעצבים את החשיבה גם עבור אדם בוגר. בתת-מודע הוא פשוט לא מבין שניתן להתייחס שונה לעולם. הכל במונחים של אמונה ודת. כך שהתוקפנות שלך היא לריק. 192.114.105.254 14:30, 29 באוקטובר 2012 (IST)

עשרות אלפי האנשים שחזרו וחוזרים בתשובה ו/או שנתגיירו, רובם משכילים ואינטלגנטים, חלקם אף מדענים דגולים, כולם יחד וכל אחד לחוד מהווים הוכחה חד משמעית לאי תקפות הטיעון שלך. טיפוסי - שו"ת 16:20, 29 באוקטובר 2012 (IST)

הגעתי לדיון הזה רק עכשיו, ואני מקדם בברכה את בנצי וטיפוסי כנציגים של 2 גישות שונות, הגישה המדעית והגישה הדתית. חברים! מקובל מאוד שכל אחד מבעלי הדעות החלוקות אוחז בדעתו, ומגן עליה כשמור לביאה על גוריה. מותר לכל אחד ממייצגי הדעות להצדיק לסנגר ולתמוך את עמדתם בכל טעם שימצאו לנכון. בד בבד על הצדדים לנהל דיון בצורה מכובדת, ולשמור ולהגן על זכותו של הצד השני לדבוק בעמדתו. כל ביטוי של זלזול בצד השני, או בעמדתו אינו מקובל לחלוטין.

אני מבקש מהמשתתפים בדיון, להסיר את הביטויים הפוגעים כגון: "כקליפת השום", "בורות", וכו'. אציין, גם קידומו בברכה של אלמוני הפוחד להזדהות בשמו, ומבזה קבוצה שלימה באשר דעתם שונה מדעתו, אינה פעולה מקובלת, ותוצאותיה אינן מבורכות. ברכות אריאל פ. (slav4) • דף שיחה 21:33, 29 באוקטובר 2012 (IST)

אריאל יקר, אני מציע ומבקש שתשקול את עמדתך לגבי אופי קיום דיונים, אין חולק על כך שהכללים מונעים ביזוי אמונתו ודעתו של חבר בקהילה, שזה אכן חמור מאד, יחד עם זאת העברת ביקורת על התנהלות היא בוודאי בגדר המותר ולעתים אף רצוי, כמו כן ציון עובדות גם אם הן לא נעימות הוא דבר מותר ולרוב אף הכרחי, כעת אתייחס למשפט שאתה מבקש ממני לשנותו "..כשמשוים אותן (הנחות המדע) לסיפור הבריאה התנכ"י הן באמת שוות כקליפת השום, בעיני היהודי המאמין כמובן". זה מקרה קלאסי של ציון עובדה יבשה, בסוגיה פילוסופית פולומוסית, זאת מבלי לפגוע באיש באופן ספציפי. מדוע הדרישה לשנות את המינוח? נראה לי שמדובר ברגישות יתר מיותרת, בויקיפדיה כמו בעולם הגדול יכולות להיות דעות שונות ומנוגדות שחלוקות בתכלית האחת מרעותה, אין בכך כל פסול למיטב שיפוטי את הכללים, ואני חושב שרבים יסכימו עמי, ולסיום, אני מדגיש שוב ששימוש בהערות מבזות ומתנשאות לגופו של ויקיפד, הוא נוהג פסול שיש לגנותו ולשרשו מקרבנו, אסור לערבב בין המקרים. ואגב שים לב למהלך הדיון, אני התנסחתי כשקיבלתי תשובות לשאלתי בסגנון "מה רבו מעשיך השם" בתגובה הופיע אנונימי שהתפלא על כך שישנם אנשים שמשוכנעים שהעולם נברא רק לפני כמה אלפי שנים, וביטל את אמונתי, זה לא הכי נעים אבל לדבריי זה לגיטימי, בתגובה לכך הגבתי שמי שמאמין בתורה השערות המדע בשבילו הן כקליפת השום, גם לא הכי נעים לצד השני, אבל שוב, לגיטימי, וכך הלאה וכך הלאה, ולסיכום, הבעת עמדה או דעה או ציון עובדה כללית או טענה כזאת היא לגיטימית גם אם היא מנוסחת בלשון חדה, ובתנאי שאין היא מתייחסת לגופו של איש, אלא לגופה של דעה או עמדה. בתקווה שדבריי יובנו כהלכתם. בברכה. טיפוסי - שו"ת 22:50, 29 באוקטובר 2012 (IST)

שאלה בגבולות

הגבול הראשון הוא נתון. אני אמור למצוא מה הגבול של השני - פיתחתי אותו לצורה השלישית. ואני שואל אם אני יכול להניח שהפרמטרים זניחים כש-X שואף ל-0. האם ההנחה שלי נכונה? ואם לא, אז מה אפשר לעשות? אביעד‏ • שיחה 08:10, 26 באוקטובר 2012 (IST)

הבנתי שטעיתי. sin(kx)/x כש-x שואף ל-0, יהיה שווה k. אך כיצד אפשר להוכיח זאת? אביעד‏ • שיחה 08:59, 26 באוקטובר 2012 (IST)

נגיד שאתה רוצה לחשב את הגבול של sin2x/x. נסמן 2x=u, אז הגבול שאנחנו רוצים לחשב שווה לגבול של:

sinu/(u/2)

ששווה לגבול של 2sinu/u. מוציאים 2 מחוץ לגבול ומקבלים שזה שווה לפעמיים הגבול של sinu/u, דהיינו 2. אגב, יכולת להשתמש בזה ישירות בלי לעבור מהגבול השני לשלישי. 94.159.182.160 09:58, 26 באוקטובר 2012 (IST)

אני לא מבין איך זה עוזר. הגעתי ל-sinu/u, וגם הוצאתי את ה-2, אבל עדיין u שואף ל-0. גם המונה, וגם המכנה, אז איך אני יודע מהו הגבול? אביעד‏ • שיחה 11:34, 26 באוקטובר 2012 (IST)

כתבת שנתון לך שהגבול של sinx/x שווה אחד. אם אתה רוצה את ההוכחה, ראה הגבול של sin(x)/x. בברכה, 94.159.182.160 11:37, 26 באוקטובר 2012 (IST)/

תודה. אביעד‏ • שיחה 07:46, 27 באוקטובר 2012 (IST)

פוטנציאל

באופן כלל, בלי לקשר לחשמל, מכניקה או תרמו: מהו פוטנציאל בפיזיקה? תנו הסבר ברמה שאוכל להסביר לילד נבון בתיכון. 109.64.188.100 09:52, 26 באוקטובר 2012 (IST)

באופן כללי אין הבדל משמעותי בין משמעות המילה פוטנציאל בפיסיקה לבין המשמעות שלה בעיברית (או באנגלית). אולי הדבר היחיד הוא שבדרך כלל בפיסיקה מדובר על אנרגיה. ירון ק. - שיחה 11:14, 26 באוקטובר 2012 (IST)

ומה המשמעות שלו? מה זה הגודל הפיזיקלי "פוטנציאל"? 109.64.188.100 11:22, 26 באוקטובר 2012 (IST)

למונח "פוטנציאל" שימושים רבים בפיזיקה, כפי שאפשר לראות מהדף פוטנציאל. השימוש הנפוץ ביותר מתייחס לאנרגייה פוטנציאלית, ובפרט לאנרגיה פוטנציאלית חשמלית. בלנק - שיחה 18:12, 26 באוקטובר 2012 (IST)

א. לצערי, שתי התשובות שנתנו קודמיי חלקיות מאוד, ולא מתמקדות בהגדרה הפורמלית המדוייקת של גודל זה. להפנות לערך הקיים זה בסדר, אבל מעבר לציון ה'שימושיות' בהמשך התשובה, אין מענה לשאלת השואל, שנאלץ לחזור ולחדד את שאלתו.

ב. ההגדרה הבסיסית של פוטנציאל בפיזיקה (ואין זה כך בתחומי דעת שאינם מבוססים על פיזיקה) היא אנרגיה פוטנציאלית ליחידת תכונה פיזיקלית פנימית של הגופים הרלוונטיים ("תכונה פיזיקלית פנימית" - למשל, מסה במקרה של אנרגיה פוטנציאלית כובדית (או אנרגיית גובה במודלים פשוטים), ומטען חשמלי במקרה של אנרגיה פוטנציאלית חשמלית). המשמעות הפיזיקלית המיידית של הגדרה זו היא העובדה שפוטנציאל הוא תכונה של המרחב בו נמצא הגוף המושפע, ולא של הגוף עצמו - שכן מדובר באנרגיה ליחידה.

מאחר והזכרת תלמיד תיכון, אוסיף שאני נוהג להמחיש זאת לתלמידיי באמצעות הדוגמא הבאה: נניח שקבוצת תלמידים מבקשת לבקר במוזיאון ארצות המקרא בירושלים. נניח גם שמחיר כרטיס כניסה הוא 50 ש"ח (אינני מעודכן) ושאין הנחה לקבוצות. כעת נשאל: מהו המחיר הכולל שתשלם הקבוצה, ומהו המחיר שישלם תלמיד יחיד ? התשובה לשאלה הראשונה אנלוגית לאנרגיה הפוט' הכוללת, והיא כמובן, תלויה בגודל הקבוצה. התשובה לשאלה השניה לעומת זאת, אנלוגית לפוטנציאל, מאחר והיא 'תכונה' של האתר ולא של גודל הקבוצה. Cest Tout !

ג. בתחומי דעת אחרים משמעות המושג 'פוטנציאל' היא כללית יותר, ומתייחסת ליכולת חבויה של עצם או מערכת עצמים. משמעות זו שונה, שכן ההגדרה הפיזיקלית מדברת על תכונה של המרחב דווקא, ואילו כאן ההגדרה דומה יותר להגדרת מושג האנרגיה הפוטנציאלית בפיזיקה. שבת שלום, בנצי - שיחה 19:09, 26 באוקטובר 2012 (IST)

לפוטנציאלים תרמודינמיים משמעות אחרת מזו שתיאר בנצי. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

א. הערתך מאוד במקומה, אבל קביעתך אינה נכונה. אני מקווה שעיינת בערך אליו הפנית. אין מדובר בהגדרה נוספת או משמעות אחרת של 'פוטנציאל', אלא בשימוש מקוצר, מושאל, ל'אנרגיה פוטנציאלית' של מערכת מרובת חלקיקים. זה אכן מבלבל במקצת, אבל המונח 'פוטנציאל' משמש שם במובן של 'אנרגיה'. תודה על הערתך.

ב. ואם כבר, שימוש דומה מקוצר במושג 'פוטנציאל' במובן של 'אנרגיה פוטנציאלית', קיים גם במכניקת הקוונטים (למשל, בור פוטנציאל) ובפיזיקה של מצב מוצק (למשל, פוטנציאל סריג). שבוע טוב, בנצי - שיחה 00:24, 28 באוקטובר 2012 (IST)

קוונטים, א"ה

אתם יודעים במקרה למה בפיתוח פה יש את 2 המעברים שסימנתי בשאלה? 109.64.188.100 11:25, 26 באוקטובר 2012 (IST)

בראשון הפעילו את האופרטורים בקצוות כל אחד לכיוון אחר והשני זה יחס החילוף שלהם.ירון ק. - שיחה 08:21, 27 באוקטובר 2012 (IST)

סריגי בראבה

סריג ברווה בו מימדי

בתמונה מוויקי האנגלית, בצד שמאל: מה ההבדל בין סריג 1 לבין סריג 3? אני רואה את המלבן שהם שרטטו, אבל לא ממש מבין את ה"חשיבות שלו". שתיהם מתארים מקביליות, לא? Corvus,(שיחה) 18:37, 26 באוקטובר 2012 (IST)

אני לא בטוח במאה אחוז שזה הענייין אבל כשהזווית של המקבילית חדה זה משנה מיהו ה"שכן הבא" NNN ולכן את הגדרת תא היחידה. ירון ק. - שיחה 08:26, 27 באוקטובר 2012 (IST)

הסימטריות של הגבישים הן בעלות חשיבות מכרעת לתכונות החומר. במקרה הזה, לסריג 1 אין סימטריית שיקוף (מראה) אלא רק סימטריות סיבוב ב-180 מעלות והזזה. לסריג 3 יש שיקוף בנוסף. ‏Setreset • שיחה 10:54, 28 באוקטובר 2012 (IST)

פונקציה הפיכה

הפכתי את הפונקציה הראשונה, וקיבלתי את השנייה. איך אני יודע אם לקחת את הפלוס או המינוס, והאם היא תקינה גם בלי לבחור? אביעד‏ • שיחה 08:05, 27 באוקטובר 2012 (IST)

שני הפתרונות נכונים (בתנאי שתצמצם ב-2!), ואפשר לבחור ביניהם אם נתונה נקודה שבה הפונקציה ההפוכה עוברת. עוזי ו. - שיחה 22:31, 27 באוקטובר 2012 (IST)

עוזי, האם בהכרח נכון בכל תחום ההגדרה? משרטוט שלוש הפונקציות, נראה שיש תחומים שבהם רק אחת מהפונקציות ההפוכות היא אכן ההופכית. ירון • שיחה 23:42, 27 באוקטובר 2012 (IST)

צריך להזהר בבחירת הסימנים. כדי להיפטר מאחד הסיבוכים, נחליף את y בהפכי שלו. נסמן $\ f_{\alpha }(x)=x+\alpha {\sqrt {1-x^{2}}}$ ו-$\ g_{\beta }=(y-\beta {\sqrt {2-y^{2}}})/2$ (עבור $\ \alpha ,\beta =\pm 1$). הקבוצות $\ \{(x,y):y=f_{1}(x)\ {\mbox{ or }}\ y=f_{-1}(x)\}$ ו-$\ \{(x,y):x=g_{1}(y)\ {\mbox{ or }}\ x=g_{-1}(y)\}$ מתארות שתיהן את אותה אליפסה, למרות שלאף שתי פונקציות אין אותו גרף. הן הופכות זו את זו מקומית בכל נקודה, אבל מי שישרטט את ההרכבה $\ g_{1}(f_{1}(x))={\frac {1}{2}}(x+{\sqrt {1-x^{2}}}-{\sqrt {1-2x{\sqrt {1-x^{2}}}}})$ יגלה שהיא מתלכדת עם פונקציית הזהות עבור $\ -1\leq x\leq {\frac {\sqrt {2}}{2}}$ אבל לא עבור $\ {\frac {\sqrt {2}}{2}}<x$. עוזי ו. - שיחה 21:59, 29 באוקטובר 2012 (IST)

וקטורי יחידה בקואורדינטות כדוריות

מה המשמעות של וקטורי יחידה בקואורדינטות כדוריות? r, לדוגמה, מייצג רק את המרחק אל הנקודה, ולא את הכיוון שלה. אז מה המשמעות של וקטור יחידה בכיוון r? תודה, 94.159.247.99 19:15, 27 באוקטובר 2012 (IST)

וקטור יחידה r הוא וקטור מראשית הצירים לנקודה מסוימת, בגודל 1. וקטורי תטא ו-פי הם המשיקים למעגלים שמרכזם בראשית באותה הנקודה. ‏Setreset • שיחה 23:28, 27 באוקטובר 2012 (IST)

תודה. 94.159.247.99 11:00, 28 באוקטובר 2012 (IST)

כיצד מדדו בעבר חום של חפצים כלשהם?

איך בעבר מדדו חום? וכי לפני גליליאו גלילי לא היה ניתן לתאר מדות חום? (לפי הכתוב בויקיפדיה ערך מדחום, הראשון שהמציא את מד החום היה גליליאו) מוטיבציה - שיחה 22:29, 27 באוקטובר 2012 (IST)

חום (פיזיקה) הוא לא תכונה של מערכת! בדיוק כמו שעבודה (פיזיקה) לא תכונה של מערכת. אי אפשר למדוד חום ישירות אלא רק את ההשפעה שלו על מערכות אחרות, כלומר שינוי בטמפרטורה. מד טמפרטורה הוא מכשיר הרלוונטי למדידת הטמפרטורות וכמו שכתוב בערך גליליי באמת אחראי על ההמצאה. אני לא יודע אם הוא בכלל השתמש במעלות כלשהם. ובכלל, לפני תחילת התרמודינמיקה מדענים בקושי התעסקו עם חום. סקלות טמפרטורות שלנו התפתחו במאה ה18-19 ככה. לפני זה לא חשבו על טמפרטורה במונחים של "כמות". Corvus,(שיחה) 14:20, 28 באוקטובר 2012 (IST)

ויי, כמה שאני רוצה להבין את דבריך, אבל אני מנסה וקשה לי, כי השפה שלך מאוד גבוהה לי. (אני אשמח ללמוד שפה גבוהה, אבל שיהיה לידה תרגום). כתבת ש"חום הוא לא תכונה של מערכת", ניסיתי להבין למה התכוונת בתכונה ולמה התכוונת במערכת. (אני מבין את כל אחת מהמילים בנפרד אבל לא בהקשר הזה). לגבי מה שכתבת שאתה לא יודע אם הוא השתמש בכלל במעלות כל שהן, אתה מעלה נקודה חשובה שלא נתתי את דעתי עליה. איך ניתן לבדוק זאת? מוטיבציה - שיחה 17:09, 28 באוקטובר 2012 (IST)

אני מצטער, לא ניסיתי "להישמע חכם" ולהפגיז במילים מסובכות. פשוט מילים כמו מערכת, חום, סביבה וכדו' נמצאים בלקסיקון שלי די קבוע. אז: מערכת במקרה שלנו זה הגוף (או קבוצת גופים) שאותו חוקרים. לדוגמה מיכל גז חם, או דלי עם מים קרים וכדו'. המילה "מערכת" מתעלמת מכל "הסביבה"- כלמור מהחדר שבו נעשה הניסוי וכל הגופים האחרים שאותם לא חוקרים כרגע (יש הרבה מאוד דברים במעבדה, אבל רק הכלי שאת הטמפרטורה שלו בודקים זה "מערכת"). תכונה זה גודל פיזיקלי שמאפיין את המערכת ברגע נתון. לדוגמה מהירות, לחץ, טמפרטורה, גובה מעל פני הים. חום לאומת זאת אינו גודל שמאפיין את המערכת. חום זה גודל שמתאפיין בכך שהוא עובר ממערכת אחת לאחרת. זה סוג של "אינטראקציה" בין מערכות שונות. לכן למערכת אחת לא יכול להיות חום. Corvus,(שיחה) 17:21, 28 באוקטובר 2012 (IST)

עכשיו אני מבין. הדברים כתובים בפשיטות ובבהירות לבעל רמה שכמוני בפיזיקה. תודה. מוטיבציה - שיחה 20:51, 28 באוקטובר 2012 (IST)

מספר שאלות ידע בכימיה

בספר הלימוד שיש לי כתוב שיחידת המסה האטומית היא: 1.6X10² (אני לא יודע איך ליצור כאן חזקה של מינוס 24, עמכם הסליחה), כלומר מסתו של אטום מימן הוא 1 ימ"א.

1. באותו ספר למדתי גם כן שמסתו של אטן נתרן היא 23 ימ"א (דלטון). ושם מוסבר ש"זהותם של האטומים נקבעת על פי מספר הפרוטונים שלהם, כלומר על פי מספר המסה", לפי דבר זה מסתו של נתרן אמורה להיות 11 ימ"א, וא"כ איך הגיעה לנתרן מסה של 23 ימ"א? אז בעצם לפי מה ניתן לדעת מה המסה של אטום?

2. לפי מיטב הבנתי כיום מניחים במדע שהגרעין של האטום הוא עגול, ולפי זה מסיקים שהרדיוס של האטום עגול, באיזו סוג של הוכחה זה מוכח אמפירית שהגרעין עגול - אולי הוא מרובע או משולש?

3. איך למעשה חישבו את המסה של אטום המימן והגיעו למסקנה הכל כך מדוייקת הנ"ל, זה מסקרן אותי להבין את זה, אני כבר כמה ימים חושב על זה כל הזמן ומנסה להבין. תודה למסייעים. מוטיבציה - שיחה 23:04, 27 באוקטובר 2012 (IST)

1) המשפט הזה אינו מדויק. זהות האטום אכן נקבעת לפי מספר הפרוטונים, אבל הפרוטונים והניוטרונים של האטום תורמים במידה שווה למסת הגרעין שלו. באטום נתרן יציב יש 11 פרוטונים ו-12 ניוטרונים, ולכן המסה האטומית היא 23. יש אטומים אחרים שיש להם מספר איזוטופים יציבים, בעלי מספר ניוטרונים שווה אך כולם בעלי אותו מספר פרוטונים. המסה האטומית של האטום מחושבת ע"י ממוצע משוקלל של מסת האיזוטופים השונים. 3) ראה en:Avogadro constant#Measurement. מרגע שאתה יודע שב-12 גרם פחמן יש מספר אבוגדרו של אטומים, אתה יודע מה מסת אטום יחיד. 94.159.247.99 23:18, 27 באוקטובר 2012 (IST)

1) במלים אחרות המשפט כפי שצוטט שגוי (אולי הציטוט לא מדויק?). מספר הפרוטונים לא שווה למספר המסה (פרוטונים+ניוטרונים), אלא מספר המסה ברוב האטומים גדול פי 2 ויותר ממספר הפרוטונים. 2) האטום, וגם גרעין האטום, בקירוב עגולים. אחד לא נובע מהשני. זה לא נבדק באופן ישיר, אבל הרבה גדלים פיזיקליים אחרים שנובעים מאותה תיאוריה כן הוכחו לאורך ניסויים רבים, כך שסוברים שכל התוצאות של התיאוריה, גם אלו שאינן יכולות להיבדק באופן ישיר, נכונות. ‏Setreset • שיחה 23:34, 27 באוקטובר 2012 (IST)

לגבי הציטוט, בדקתי שוב והחלטתי להביא אותו לפניכם במלואו: "זכרו שזהותם של האטומים נקבעת על פי מספר הפרוטונים (הדגש במקור. מ.), כלומר על פי מספר המסה. מסתם, לעומת זאת, נקבעת על פי סכום (הדגש במקור. מ.) הפרוטונים והנייטרונים. לכן ייתכנו שני אטומי פחמן אשר לאחד מהם 6 נייטרונים ולשני 8 נייטרונים. המספר האטומי שלהם, כלומר מספר הפרוטונים הוא זהה (6) שכן שניהם אטומי פחמן. היות שמספר המסה שלהם שונה, בשל השוני במספר הנייטרונים, גם המסה שלהם שונה." (אפרופו "האומר דבר בשם אומרו", דברים אלה לקוחים מתוך הספר "בסביבת הכימיה" 2009 שנכתב בידי ד"ר דבורה יעקובי, רכזת ההוראה בחמד"ע, עורכת מדעית בכתב העת "סיינטיפיק אמריקן ישראל", ממקימי האונ' הפתוחה, והייתה שותפה בכתיבת הקורסים הראשונים של אוניברסיטה זו. התמחותה בכימיה פיזיקלית (תואר שני), ובביוכימיה (תואר שלישי)). מוטיבציה - שיחה 23:54, 27 באוקטובר 2012 (IST)

א. נתחיל מעשיית סדר מושגי. בדומה למה שכבר הסבירו קודמיי, אם כי בצורה חלקית ולא ממוקדת דייה, מבחינים בין מספר אטומי, שהוא מספר הפרוטונים בגרעין, ובין מספר מסה, שהוא מס' הנוקליאונים (מס' פרוטונים + מס' נויטרונים) בגרעין האטום. הגדרות אלה אינן מקריות: המס' האטומי (מס' הפרוטונים בגרעין) קובע את תכונותיו הכימיות (יכולת קישור ופעילות כימית) של האטום, ואילו מס' המסה קובע את תכונותיו הפיזיקליות של האטום (אני מתעלם כרגע מקיומם של איזוטופים שונים, שאינו רלוונטי לשאלתך). הנוסח שאתה מצטט הוא אכן שגוי (וריבוי התארים לא יכול לשנות עובדה זו).

ב. אני שמח על הערתך ועל הצפת שגיאה מודפסת זו. כמי שעוסק בהגהה של ספרות לימוד מדעית, בין היתר, אני נתקל בלא מעט מקרים מסוג זה. הבעיה אינה במשגה עצמו, כי כולנו בני אדם, ומועדים לטעויות ולתקלדות, אלא בהעדרה של מערכת יסודית ומסודרת של ביקורת עמיתים והגהה, לשונית ומדעית, שיכולה היתה לנפות משגה כזה. אדאג לפנות לאן שצריך, ע"מ להסב את תשומת הלב לצורך לתקן זאת במהדורות הבאות, ובינתיים, להוסיף דף תיקונים למהדורה הנוכחית (אני מקווה שעיינת בדף התיקונים המצורף, בדר"כ, לספר הלימוד; מאוד יתכן ומופיעה שם כבר הערה בעניין הנדון). שבוע טוב, בנצי - שיחה 00:53, 28 באוקטובר 2012 (IST)

תודה בנצי על הסדר והמושגים. למען האמת, לך ולי יש כבר 'היסטוריה' במציאת שגיאות כאלה, ראה כאן לגבי ספר הלימוד בפיזיקה של ד"ר יבגני. הצעתך לעיין בתיקונים הייתה נעשית ברצון אילו היו כאלה, אך אין כאלה בספר הלימוד שבידי (אגב, האם אתה כותב את המילה נייטרון כ"נויטרון" בכוונה או שזו תקלדה?) שבוע טוב. כמו כן לכל המשיבים תודה רבה על תרומתכם לבירור הנושא וליבונו. מוטיבציה - שיחה 01:18, 28 באוקטובר 2012 (IST)

תיקון לדברי שלמעלה: לגבי צורת אטומים, לפעמים הם ממש לא עגולים. ראה אורביטל ואטום המימן, יש שם איורים של צורות אפשריות שונות, וכפי שאפשר לראות, לא ממש כדוריות. ‏Setreset • שיחה 06:57, 28 באוקטובר 2012 (IST)

תודה על התיקון. בכל אופן, הגעתי למסקנה שהפיזיקה לא מספיק מפותחת בתיאור מוכח של החומר אותו היא מתארת. תיאוריות רבות נשענות על הסתברויות, ובהיעדר יכולת לבדוק הסתברויות אלה ולהוכיח אותן אמפירית, רבים מן הדברים האלה הם 'בהנחה' שכך הוא המצב. קשה מאוד ללמוד כך. לרבים מן השאלות הפשוטות כביכול בפרט בפיזיקה גרעינית אין תשובות מוכחות, אחת מהן זו שאלת הצורה של הגרעינים ושל חלקיקי האטום בכלל. מוטיבציה - שיחה 16:55, 28 באוקטובר 2012 (IST)

אתה מבולבל בנושא ההסתברות. יש שני ביטויים של הסתברות בפיזיקה. האחד הוא במכניקה סטטיסטית שם החישובים הם אכן סטטיסטיים, אבל לא כי אין תורה מדויקת מאחוריהם, אלא כי יותר נוח ומעשי להשתמש במודל סטטיסטי מקורב ומוצלח מאשר להשתמש במודל מדויק לחלוטין אבל כמות הנתונים בו ואורך החישובים בו גדולים מידי גם בשביל כל מחשבי העולם יחד. השני הוא במכניקת קוונטים, ששם גם חישובים פשוטים הם הסתברותיים, אבל לא כי למדענים אין הבנה מעמיקה מספיק של המציאות, אלא כי (ככל הידוע) הטבע עצמו עורך הגרלות שקובעות את התוצאה באקראי. עובדה היא שמכניקת קוונטים, על אף ההסתברויות שבה, חוזה תוצאות של ניסויים באופן מדויק יותר מכל תורה אחרת בהיסטוריה האנושית. לגבי צורת האטום (שנקבע על פי האלקטרונים ולא לפי הגרעין), העובדה שהוא עגול אינה הנחה מקרית, אלא מסקנה מניסויים רבים שבוחנים את התחזיות המתקבלות מטענה כזו. אין דרך אחרת לאשש זאת. דניאל • תרמו ערך 19:07, 28 באוקטובר 2012 (IST)

אני מבין את מה שאתה אומר, אבל לפחות ברמה ההשכלתית פיזיקלית שבה אני נמצא כעת, קשה לי לקבל זאת כהבנה מעמיקה של המציאות בקרב המדענים. בדברים חומריים הורגלנו גם את וגם אני, לחוש אותם כדי לאמת שהם אכן קיימים. הפיזיקה מציעה יותר מדאי מודלים המונחים על אקסיומות שלא ניתן להפריך אותם. כך לדוגמה אם תאמר שהאטום הוא מרובע, ומישהו אחר יאמר שהוא עגול ואני אומר שהוא משולש, ההוכחה היחידה תהיה אם נראה אותם דרך מיקרוסקופ, או משהו שמוכיח זאת, כמו לדוגמה טביעה שמשאיר האלקטרון או כל דבר אחר שמוכיח את צורתו. יוצא לי לשאול מדענים רבים בעלי תארים מתקדמים, ואני שם לב שאין שם תמימות דעים בנוגע לדברים כה יסודיים הנוגעים לפיזיקה אטומית. הרבה פעמים אני חושב לעצמי על כך שאין לי בעיה עם זה שלא יודעים, אבל לפחות שלא יציגו מצג שוא כביכול שכאילו הכל ידוע והם שולטים במצב. דברים יסודיים לא ברורים ולא מוכחים (לי). {דברי כתובים ברוח טובה מתוך מטרה להתדיין ולא להתנצח, נא להמשיך ברוח זו בבקשה} מוטיבציה - שיחה 19:47, 28 באוקטובר 2012 (IST)

אם בא מדען וטוען שהאטום קובייה קל להפריך את טענתו. עורכים ניסוי שתוצאותיו מושפעות מצורת האטום ורואים אם התוצאות הן כפי שנחזו על ידי קוביה או כפי שנחזו על ידי כדור. ואכן כשעורכים ניסוי כזה התוצאה היא כדור (וחשוב לציין שאנו עוסקים באטומים שאינם חלקיקים יסודיים ויש להם נפח, כך שיש בכלל מובן לאמירה שיש להם צורה). אתה חייב להתנער מההסתמכות על חוש הראיה. בפיזיקה ראיות המובססות על ראיה הן מהזן הנחות ביותר. ראיה היא בסך הכל מכשיר מדידה אופטי העושה שימוש בפוטונים ועובר עיבוד אינטרסנטי על ידי המוח. זוהי עדות חלשה לאין שיעור מכלי מדידה במעבדה. אני לא מבין על איזה בלבול אתה מדבר. פיזיקה גרעינית מודרנית היא תחום מבוסס מאוד שעולה בקנה אחד עם כל המדידות והניסויים שנעשו במהלך ההיסטוריה. היא מפיקה ניבויים מדויקים שטכלונוגיות שימושיות רבות מבוססות עודותם. המצג שווא שאתה טוען שישנו אינו קיים. דניאל • תרמו ערך 19:56, 28 באוקטובר 2012 (IST)

החלטתי למספר את דבריי בהתייחס לדבריך המלאים תוכן לימודי בשבילי.

1. אשמח לקבל מידע על צורת הניסוי שבה התוצאות מושפעות מצורת האטום ורואים בה אם התוצאות מתאימות לקוביה או לכדור. זה מעניין אותי לאין ערוך.

2. שמתי לב לכך שהתסייגת וכתבת שחשוב לציין שאנו עוסקים באטומים שאינם חלקיקים יסודיים ויש להם נפח, כך שיש בכלל מובן לאמירה שיש להם צורה. מכלל הן אני למד על לאו. האם ניתן להבין מדבריך שלחלקיקים היסודיים (כדוגמת פרוטון ונייטרון) אין נפח? איך ייתכן איפוא שאפס נפח ייצור 1 נפח?!

3. הדהמת אותי במשפט: "בפיזיקה ראיות המבוססות על ראיה הן מהזן הנחות ביותר". חשבתי עד עתה להפך. ועכשיו אני מתחיל להטות את דעתי לדבריך, אך נצרכת לי דוגמה לראיה חזקה יותר מאשר ראייה.

4. אם טעיתי בעניין מצג השווא, תלון משוגתי עמי. אני לומד הרבה וביזע כדי להבין את עולם הפיזיקה. האמן לי. אמנם אני רק בהתחלה של ההתחלה, ולכן דון אותי לכף זכות עם דעותיי. 20:47, 28 באוקטובר 2012 (IST)

חלק מהגילויים החשובים ביותר בהיסטוריה של הפיזיקה הושגו בעקבות ההבנה שפעמים רבות יש הבדל בין האופן שבו המוח האנושי תופש דברים אינטואיטיבית לבין האופן שבו הטבע פועל. במשך כ-2000 שנה, מאז ההוגים היוונים הראשונים, היה ברור לכולם שכדי שגוף ינוע, צריך להפעיל עליו כוח, וש"המצב הטבעי" של גוף שלא פועל עליו כוח הוא מנוחה. לקח הרבה מאוד זמן עד שבמאה ה-16 התגבשה ההבנה שכוח אינו דרוש כדי לשמור על מהירות קבועה, ושגוף שלא יפעל עליו כוח יתמיד במהירותו. 94.159.247.99 20:55, 28 באוקטובר 2012 (IST)

ניסוי פיזור מוכיח את צורת האטום או הגרעין, תלוי בסוג החלקיקים שמפזרים והתנע שלהם. כדוגמה הכי פשוטה, ניסוי רתרפורד הפריך את מודל עוגת הצימוקים של האטום. ‏Setreset • שיחה 21:55, 28 באוקטובר 2012 (IST)

1. סטריט ענה.

2. אני לא רוצה להיכנס לסוגיה הזו כי איני פיזיקאי ואני מפחד לטעות. בכל אופן רוב הנפח באטום הוא הריק שבין החלקיקים היסודיים, כך שייתכן שלחלקיקים יסודיים נפח 0 ולאטום נפח חיובי.

3. קל לתת דוגמאות מחיי היום יום. על מה תסמוך יותר? אדם שמודד את זמן הריצה של אצן 100 מטר באמצעות שעון עצר או מכשיר אופטי שעושה זאת (כמו באולימפיאדה). דניאל • תרמו ערך 18:59, 29 באוקטובר 2012 (IST)

האם יש סוף לגובה הטמפרטורה?

מקובל להניח שנקודת האפס המוחלט היא הנקודה שבה החומר נמצא במצב של אי תנועה (או לפי תורת הקוונטים החומר נמצא במצב של תנועה יסודית), נקודת האפס היא אפוא 273.15- מעלות צלזיוס, 459.67- מעלות פרנהייט או אפס קלווין (כך לפי הערך האפס המוחלט), שאלתי היא האם יש סוף לקצה השני של המדידה, כלומר האם יש מעלה כלשהיא שהיא שיא המהירות שבה חלקי החומר יכולים לנוע (בדומה לאפס המוחלט אלא ההפך ממנו)? מוטיבציה - שיחה 02:57, 28 באוקטובר 2012 (IST)

אם אני לא טועה (לא למדתי את זה באופן פורמלי):

נתבונן אך ורק בגזים אידאליים, ללא אפקטים קוונטים ומעברי פאזות. ישנה הגבלה על מהירות החלקיק שהיא מהירות האור. כשמחממים חומר ומהירות ממוצעת של חלקיק בו מתקרבת למהירות האור, אז כל תוספת חום לא משנה כמעט את הטמפרטורה. זה נראה כמו אסימפטוטה אופקית, כלומר גבול באינסוף. במילים אחרות בגרף של "טמפרטורה" כפונקציה של "חום שמוסיפים למערכת" מתקבל שהקו שואף לטמפרטורה מקסימלית כלשהי ולא יכול להגיע אליה.

אבל, מה שחשוב לטמפרטורה זה לא מהירות החלקיק אלא התנע שלו. ולכן אין טמפרטורה מקסימלית אוניברסלית לכל החומרים, אלא לכל חומר יש טמפרטורה מקסימלית אחרת. וזאת בניגוד אפס המוחלט שהוא היחיד לכל החומרים בעולם.

כאמור, לא למדתי את זה באופן פורמלי, אז יתכן שהמסקנות שלי שגויות (למרות שלי הם נראות נכונות לוגית). Corvus,(שיחה) 14:10, 28 באוקטובר 2012 (IST)

מהו גז אידיאלי? ולא הבנתי למה זה נראה כמו אסימפטוטה אופקית, הלא במהירות האור תוספת חום לא משנה (כמעט?!) את הטמפרטורה. מה ההבדל בין מהירות החלקיק לתנע שלו? מוטיבציה - שיחה 16:46, 28 באוקטובר 2012 (IST)

הנחתי גז אידיאלי כי זה המודל הכי פשוט. קודם צריך להבין את הפשוט ואחרי זה מוספים לו סיבוכים (כגון אינטראקציה בין החלקיקים, עליה ברמה אנרגטית ומעבר למצב צבירה פלזמה (מצב צבירה)). לגבי אסימפטוטה: זה המשמעות המתמטית של אסימפטוטה אופקית- גבול שאליו שואפת הפונקציה כאשר המשתנה שלה שואף לאינסוף. אתה מתקדם בציר ה- X (כלמור מוסיף חום) ושואל "איך משתנה הY" (כלומר איך גדלה הטמפרטורה). אם התשובה היא "בXים גודלים מאוד Y כמעט ולא משתנה" אז זה אסימפטוטה. בניסוי שלנו מתקבל שבטמפרטורות גבוהות מאוד, מוסיפים חום ולא מקבלים כמעט שום שינוי בטמפרטורה. ההבדל בין תנע לבין מהירות הוא שתנע גם מתחשב במסה של החלקיקים (עבור אותו התנע חלקיק קל יותר ינוע מהר יותר). Corvus,(שיחה) 17:02, 28 באוקטובר 2012 (IST)

לדעתי קורווס טועה. אמנם יש מהירות מקסימלית לחלקיקים בגז, אבל אין אנרגיה מקסימלית (כך לפי תורת היחסות הפרטית}. לפיכך אין טמפרטורה מקסימלית לגז במובן הזה. אחת ההגדרות לטמפרטורה היא הנגזרת של האנרגיה הפנימית לפי האנטרופיה. הקשר הפונקציונלי בין הגדלים האלה תלוי במערכת הספציפית בה עסקינן. אפשר אולי לחשוב על מערכת שבה קיימת טמפרטורה מקסימלית (לא חשבתי על זה לעומק), אבל במערכת של מולקולות נעות אין כזו. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

במחשבה נוספת מערכת דמיונית כזו כנראה תפר את החוק השני של התרמודינמיקה. קשה לי להסביר מדוע, וממילא זה לא מה ששאלת. בלי קשר, ראה גם טמפרטורת פלאנק. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

חבורה ציקלית

מה המוטיבציה להגדרה של חבורה כחבורה ציקלית? למה ההגדרה היא דווקא כזו? תודה, 94.159.247.99 14:06, 28 באוקטובר 2012 (IST)

חבורות ציקליות הן החבורות הפשוטות ביותר ונוטות להופיע בהקשרים רבים (למשל המספרים השלמים עם חיבור הם חבורה ציקלית). כמו כן הן אבני הבניין מהן ניתן לבנות חבורות מורכבות יותר (למשל את כל החבורות האבליות הנוצרות סופית). זו המוטיבציה להגדרתן. למה דווקא בדרך זו? כי זו ההגדרה הפשוטה ביותר. דניאל • תרמו ערך 14:10, 28 באוקטובר 2012 (IST)

למה לדוגמה אם יש h איברים בחבורה, איבר הזהות צריך להיות שווה לאיבר שיוצר את כל החבורה, בחזקת h? 94.159.247.99 14:13, 28 באוקטובר 2012 (IST)

הטענה הזו לא מיוחדת ליוצר של חבורה ציקלית. זה נכון לכל איבר בכל חבורה סופית. ראה משפט לגראנז'. בחבורה ציקלית קל לראות את זה. אם g היוצר של החבורה, אז לפי ההגדרה איברי החבורה הם: $g^{0},g^{1},g^{2},\ldots$. אם בחבורה הזו יש h איברים אז בהכרח אחרי h+1 איברים חייבים לחזור לאיבר היחידה $g^{0}$. דניאל • תרמו ערך 14:28, 28 באוקטובר 2012 (IST)

תודה. 94.159.247.99 17:53, 28 באוקטובר 2012 (IST)

שאלה לגבי הצגה פרמטרית של פונקציה

המרצה שלי למתמטיקה (במסגרת של מבוא מתמטיקה לפיזיקאים) נגע היום בהצגה פרמטרית של פונקציה. הוא אמר שבמקום הצורה הנפוצה y=f(x) ניתן לקשר בין x ו-y באמצעות משתנה שלישי, "פרמטר" לדוגמה t.

אז הוא רשם: x=x(t), y=y(t)

הוא נתן דוגמה של אליפסה. c הוא הפרמטר. וa וb קבועים.

x=acos(c), y=bsin(c)

במקרה זה, הוא חילץ את הסינוס והקוסינוס, וקיבלנו משוואה קלאסית של אליפסה.

שאלתי היא, מדוע נקבע דווקא פרמטר שרירותי מסוים. כלומר, לי נראה שהוא פעל מתוך ידיעה שהוא רוצה לדבר את הזהות של סינוס בריבוע ועוד קוסינוס בריבוע שווה אחד. אך האם אני יכול לבחור כל פרמטר שאני רוצה? איך אני שולט בכך שאני לא אקבל משוואה הזויה. מאוד יעזור לי אם תינתן דוגמה למצב כזה עם פרבולה - פונקציה אותה אני מכיר טוב. תודה, אביעד‏ • שיחה 19:25, 28 באוקטובר 2012 (IST)

נתחיל מזה שאין מדובר בפונקציה. אליפסה אינה הגרף של שום פונקציה (כי יש ערכים של x להם מתאימים שני ערכים של y). מה שהוא עשה הוא פשוט להגדיר קבוצה במישור שהיא במקרה הזה אליפסה. זוהי הקבוצה $\{(x,y)\mid x=a\cos(c),y=b\sin(c),c\in \mathbb {R} \}$ (אני מניח שהסימון הזה מוכר לך, אמור אם לא). באופן כללי $\{(x,y)\mid x=f(c),y=g(c),c\in \mathbb {R} \}$ היא קבוצה במישור. כאשר קבוצה שכזו היא במקרה גרף של פונקציה (לעתים באופן מקומי) קוראים לה פונקציה סתומה. לרוב משפט הפונקציה הסתומה מאפשר לקבוע אילו קבוצות כאלו הן פונקציות סתומות. דניאל • תרמו ערך 19:39, 28 באוקטובר 2012 (IST)

בפרבולה ההצגה $\ y=x^{2}$ או $\ x=y^{2}$ מייתרות את הצורך בפרמטר משותף (משום שהתלות של אחד המשתנים בשני פשוטה כל-כך). אבל במקרים רבים כל הקואורדינטות תלויות בגורם חיצוני (למשל - תנועה במישור), ואז נוח מאד לתאר הכל באמצעות פרמטר. אין צורך לפתור את "המשוואה ההזויה" ולמצוא את התלות הישירה של y ב-x. עוזי ו. - שיחה 21:06, 28 באוקטובר 2012 (IST)

ראה גם מסילה (מתמטיקה). דניאל • תרמו ערך 21:11, 28 באוקטובר 2012 (IST)

תודה רבה. אביעד‏ • שיחה 21:32, 29 באוקטובר 2012 (IST)

איך להכין דגם מד טמפרטורה של גלילאו גלילי

בכוונתי לבנות דגם של מד טמפרטורה של גלילאו גלילי. מה אני צריך לעשות כדי לבנות דגם ביתי לדבר הזה? {הדבר הראשון שאני צריך זה את הטקסט שבו הוא מתאר את בניית המד הזה}. תודה לכל המסייעים בהדרכה. מוטיבציה - שיחה 19:46, 28 באוקטובר 2012 (IST)

פיזיקלי מרוכב

האם יש גודל בטבע שיכול להיות מתואר אך ורק על ידי מספר מרוכב? אני יודע שיש הרבה מאוד דברים שמסמנים במספרים מרוכבים, אבל אולי ניתן בכתוב אותם בדרך אחרת כך שהם יהיו ממשים? 192.114.105.254 14:46, 29 באוקטובר 2012 (IST)

ראה ויקיפדיה:הכה את המומחה/ארכיון198#האם גודל פיזיקלי יכול להיות מרוכב?. 94.159.247.99 16:35, 29 באוקטובר 2012 (IST)

ראוי לציין שהשימוש במרוכבים בפיזיקה ומתמטיקה רחוק מלהתמצא במדידת גדלים. אנליזה מרוכבת מעניקה לנו כלים חזקים במיוחד שעוזרים גם בבעיות "ממשיות" לחלוטין. דניאל • תרמו ערך 18:55, 29 באוקטובר 2012 (IST)

הגדרת קבוע אלסטי

האם ניתן להגדיר קבוע אלסטי k, במקרה של כבל, כמכפלת מודול יאנג בשטח החתך חלקי אורך הכבל? עם היחידות זה הסתדר... אביעד‏ • שיחה 21:34, 29 באוקטובר 2012 (IST)

כן. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 23:08, 29 באוקטובר 2012 (IST)

אכן, וראה גם חוק הוק, אבל זהו מקרה פרטי לחומרים אלסטיים או בתחום האלסטי שלהם. בנצי - שיחה 00:00, 30 באוקטובר 2012 (IST)

באופן כללי לחומרים "הוקיאנים". אבל בכל מקרה לא ניתן להגדיר קבוע אלסטי ליניארי k לחומרים שלא מקיימים את חוק הוק. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 23:43, 30 באוקטובר 2012 (IST)

פיזיקה

נגיד שאני נמצא במקום מבודד עם ריק, כלומר שאינו מושפע מתנאי מזג האוויר, או כל תנאים חיצוניים אחרים. יש לי שולחן, וחפץ כבד מאוד. (שניהם עשויים מחומר לא-אורגני, שלא נהרס או משתנה במשך הזמן). אני מניח את החפץ הכבד על השולחן. יש שתי אפשרויות ברורות:

1. החפץ כבד מדי, והשולחן מתרסק או מתעקם

2. החפץ לא כבד מדי, והשולחן מחזיק לנצח נצחים.

האם ישנה אפשרות שלישית- השולחן מחזיק תקופה מסויימת ורק אחרי זה מתרסק או מתעקם. במילים אחרות, האם החפץ מפעיל איזה שהוא לחץ או כוח או מתקף (או אחד מאלה) קבוע על השולחן, או האם רק ברגע ההנחה שלו הוא משפיע על השולחן.

אם האפשרות השלישית לא קיימת, אז איך נוצרים פצעי לחץ? אם היא קיימת, אז איך זה שאיזונים חלשים למראה, כמו זה למשל, יכולים להחזיק מעמד הרבה זמן? בלנק - שיחה 22:46, 29 באוקטובר 2012 (IST)

1. נצח זה הרבה מאד זמן; אולי הפרוטונים יתפרקו בדרך. 2. עייפות החומר היא לא רק מטאפורה. 3. גוף האדם (בפרט העור) אינו עונה לתאור "חומר לא-אורגני שלא נהרס או משתנה". עוזי ו. - שיחה 23:00, 29 באוקטובר 2012 (IST)

התעייפות אינה תופעה סטטית/קווזיסטטית אלא תופעה דינמית. במצב קווזיסטטי התופעה היא זחילה ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 23:12, 29 באוקטובר 2012 (IST)

תודה לעונים, כמה שאלות נוספות:

1. מה בעצם, ברמה החלקיקית, גורם לזחילה?

2. בערך זחילה (דפורמציה) היה כתוב שהזחילה היא גם פונקציה של הטמפרטורה. האם באפס המוחלט לא תהיה זחילה כלל?

3. האם הבנתי נכון מתשובתו של גיל, שעייפות החומר לא ממש קשורה לשאלה?

4. בכל זאת, בעניין פצעי הלחץ- מה גורם להם? הרי די ברור שלא מדובר בזחילה. כתבתי "חומר לא אורגני", כדי שלא יכתבו לי "השולחן נרקב לאורך הזמן", אבל גם העור לא נרקב תוך כמה שעות. תודה מראש. בלנק - שיחה 00:44, 30 באוקטובר 2012 (IST)

אתייחס כרגע לעניין פצעי לחץ, משום שזו שאלה נפרדת השונה מהיתר. בניגוד לצברי חלקיקים המרכיבים עצמים דומים, מערכות ביולוגיות (דוגמת תאים ורקמות) מגיבות בצורה מורכבת בהרבה. אני מניח שאתה יודע שתאי רקמות מתחדשים כל הזמן. כלומר, תאים מתים, ובמקומם מתחדשים תאים בתהליך של התחלקות. תהליך זה אינו סטטי ואינו מתקיים בקצב קבוע. קולטנים על מעטפת התא מגיבים לתנאי הסביבה, כולל תנאים פיזיקליים, כמו כבידה וכמו לחץ. הבעיה אינה בלחץ כשלעצמו, משום שאדם בריא נמצא בתנועה מתמדת, הן הגוף כולו והן אזורים שונים שלו (גם במהלך שינה). הבעיה היא במצבים בהם הלחץ המקומי או האזורי הוא קבוע לפרק זמן ממושך, דוגמת מקרים של שיתוק מלא, אובדן הכרה ממושך, פציעה קשה וכיוב'. לחץ ממושך כזה משפיע על זרימת אותות מולקולריים (בהעדר ערך עברי, עיין בערך הקצרצר הבא, ודיון מקיף ורחב יותר תמצא כאן) המכתיבים לתאים את עיתוי וקצב ההתחדשות, ומכאן פוגע בקצב ההתחלקות, ובעקבותיו - קצב ההתחדשות. בנצי - שיחה 10:14, 30 באוקטובר 2012 (IST)

זחילה בדומה להתעייפות הן תופעות שלא מובנות לחלוטין, קצת קשה לי להרחיב על זחילה כי למדתי אותו באופן שטחי וגם התעייפות, שלמדתי בכמה קורסים שונים עדיין קשה לי להיכנס לעומק העניין. אתה יכול לקרוא בערך האנגלי על מספר סוגי זחילה ועל מקור התופעה. עקרונית זחילה קוראת בטמפ' יחסית גבוהות, כלומר בטמפ' קרובה לנק' ההתכה. לדעתי (וזה בלי להתבסס על ידע אלא לפי מה שנראה לי הגיוני) לא תתפתח זחילה באפס המוחלט. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 00:11, 31 באוקטובר 2012 (IST)

הערך "מדחום גלילאו" - מדויק?

קראתי את הערך הקצרצר בויקיפדיה שנקרא "מדחום גלילאו" ומצאתי בו אי אילו דיוקים... למשל, כתוב שם: " הרעיון למדחום הועלה בתחילת המאה ה-17 על ידי גליליאו גליליי ועל שמו (על אף שהוא עצמו לא בנה כזה) קרוי המדחום.". סוף ציטוט. למען הסדר הטוב ראוי להדגיש שני דגשים:

1. גלילאו בנה מדחום, אומנם בלי סקאלה, אבל הוא בנה מדחום ואף השתכר מלימוד עשייתם. מערך זה משתמע שהוא התעסק ברעיונות גרידא. ניתן לראות זאת בויקיפדיה עצמה בערך מדחום ששם כתוב כך "גלילאו גליליי היה הראשון שבנה ב-1592 מדחום והשתמש בו בניסוייו (זאת לא אני כתבתי).

2. בשנת 1990 בערך המוזיאון להיסטוריה בלונדון פיתח משהו שנקרא "תרמומטר גלילאו", לתרמומטר זה אין קשר למדחום שגלילאו השתמש בו, הקשר הינו מקרי בלבד, והמוזיאונים קראו את זה על שמו. ראו גם ערך Galileo thermometer (אנגלית) מוטיבציה - שיחה 00:33, 30 באוקטובר 2012 (IST)

זה לא הדף המתאים לשאלות כאלה. אני מציע לך להעביר את ההערות לשיחה:מדחום גלילאו. אם לא יגיבו לך, אתה מוזמן להפנות אנשים לדיון מויקיפדיה:לוח מודעות. לאחר מכן אתה מוזמן גם לשנות בעצמך את הערך, בהתבסס על מקורות. בהצלחה בלנק - שיחה 00:48, 30 באוקטובר 2012 (IST)

גאומטריה בתלת מימד

אני צריך לסדר כדורים זהים ברדיוס $a/2$ כמה שיותר צפוף. מטרה שלי היא לחשב את הגובה של מרכז הכדור משכבה העליונה ביחס לשכבה התחתונה.

אני יושע שהסידור האופטימלי הוא "סידור כדורי תותח". כלמור מצמידים 3 כדורים ושמים מעליהם עוד חד בתוך השקע. ברביעיות כאלה מרצפים את המישור ואז ממלאים את השכבה הבאה בכדורים באותו האופן, מקבלים שליליות וממשיכים האלה. אני לא יודע איך להוכיח שזה הסידור בעל הצפיפות המקסימלית, למרות שזה נשמע לי מאוד אינטואיטיבי.

ולא יודע כיצד לחשב את היחס בין רדיוס הכדור לבין "הגובה", כלומר מרחק בין השכבות. 79.181.212.218 18:20, 30 באוקטובר 2012 (IST)

זוהי השערת קפלר שהיתה חלק מרכזי בבעיה ה-18 של הילברט . הבעיה נפתרה לפני כמה שנים (ע"ע באנגלית); אל תצפה להוכחה קלה או פשוטה. עוזי ו. - שיחה 18:55, 30 באוקטובר 2012 (IST)

השאלה היא במקור כאן והיא באה מקריסטלוגרפיה. אם אתה אומר שזה באמת שאלה שקשה מאוד להוכיח אז לא סביר להניח שלא היו נותנים אותה בש"ב. אז נניח שאני מקבל כנתון שהמבנה האופטימלי הוא HCP. איך מזה אני מוצא את היחס בין a לc? חשבתי על זה וניסיתי לשרטט, זה נראה כמו טטראדר שבו אני צריך למצוא את הגובה אם אני יודע את הצלע. אבל יוצא $c={\sqrt {6}}/3$. מאיפה יכול לבוא היחס שהם מבקשים? 79.181.212.218 19:31, 30 באוקטובר 2012 (IST)

בשאלה לא מבקשים שתמצא את הסידור האופטימלי (=בעיית קפלר, קושי 48), אלא את הסידור הטוב ביותר מבין הסידורים בסריג הקסגונלי (=בעיית שעורי בית, קושי 12). עוזי ו. - שיחה 21:49, 30 באוקטובר 2012 (IST)

לא ממש הבנתי מה ההבדל. הסידור הכי טוב הוא הסידור ההקסגונלי, לא? או שיש מספר סידורים בשם "הקסגונלי" ואחד מהם הוא "הטוב ביותר" ( ואיך מוצאים אותו?)? 79.181.212.218 22:07, 30 באוקטובר 2012 (IST)

איך מחושב המספר של דרגת הקושי? זה סולם מוכר? --46.117.105.50 20:58, 31 באוקטובר 2012 (IST)

The Art of Computer Programming. ראה כאן, עמודים 9-11. עוזי ו. - שיחה 23:01, 31 באוקטובר 2012 (IST)

מכפלה בין מטריצות

מכפלה בין מטריצות נותנת מטריצה, נכון? איך קוראים לסוג מכפלה כזה? חשבתי שזה "מכפלה פנימית", אבל פנימית חייבת לתת סקלאר ופה המכפלה מכזירה אותנו למרחב המטריצות. 79.181.212.218 21:02, 30 באוקטובר 2012 (IST)

למה כוונתך במלה "סוג"? הכפל הרגיל של מטריצות נקרא, עד כמה שזה מוזר, כפל מטריצות. עוזי ו. - שיחה 21:47, 30 באוקטובר 2012 (IST)

המודל נפל?

על פי מודל הנלמד במערכת החינוך, כל מולקולה אשר אינה סימטרית, (כמו פרמידה משולשת למשל) קוטבית. אבל מה קורה עם לאטומים המרכיבים את המולקולה יש ערך אלקטרושליליות דומה? כך לדוגמה ב-NCl3 לחנקן וכלור יש ערך אלקטרושליליות דומה. על כן אין כמעט קוטביות בקשר. אבל בגלל זוג האלקטרונים הלא קושרים של החנקן כן מתקיימת פרמידה משולשת. אז האם המודל של משרד החינוך נפל? Exx8 - שיחה 20:57, 31 באוקטובר 2012 (IST)

תאוצה

שאלה במכניקה:

אני נמצא על קיסקה שאני רוצה לבדוק האם היא נעה בתאוצה קבועה או מסתובבת. איך אני עושה ניסוי שיוכיח לי חד משמעית באיזה סוג תנועה אני (מבין 2 האפשרויות). מהם מכישרי המדידה המתאימים? הדיסקה יחסית גדולה ורוצים ניסוי לא מקומי. אין אפשרות לתקשר עם הסביבה החיצונית לדיסקה. 79.177.217.142 21:26, 31 באוקטובר 2012 (IST)

מה המונח העברי המקביל למידה SPAN?

מהו המונח העברי המקביל, למידה span? מוטיבציה - שיחה 23:36, 31 באוקטובר 2012 (IST)

זרת (יחידת מידה). עוזי ו. - שיחה 23:50, 31 באוקטובר 2012 (IST)

תודה. מוטיבציה - שיחה 22:48, 1 בנובמבר 2012 (IST)

החוק הראשון של ניוטון

אם יש את החוק השני, למה צריך את החוק הראשון? ברור שאם F=ma ואין כוח אז a=0 . אז למה לא הסתפק ב2 חוקי ניוטון? 192.114.105.254 10:34, 1 בנובמבר 2012 (IST)

אפשר לחזק את שאלתך. חוקי ניוטון תקפים אך ורק במערכת אינרציאלית, כלומר, מערכת בה גוף שלא פועלים עליו כוחות לא משנה את מהירותו. אבל זהו בדיוק החוק הראשון של ניוטון. במילים אחרות, החוק הראשון של ניוטון קובע שבמערכת יחוס שבה הוא מתקיים הוא אכן מתקיים. זו, בעיני, טאוטולוגיה. אני אישית מבין את החוק הראשון של ניטון כקובע שקיימת מערכת ייחוס אינרציאלית, שבה מתקיים החוק השני. (זה בכלל לא מובן מאליו, ובכלל, קשה להוכיח שזה נכון בכלל). הבעיה היא שזה לא מה שניוטון אמר... אני גם מוטרד לעיתים מהשאלה הזו. משה פרידמן - שיחה 10:48, 1 בנובמבר 2012 (IST)

לשואל: זה שכוח יוצר תאוצה לא אומר שהוא הדבר היחיד שיוצר תאוצה. החוק הראשון נועד להגיד שאין שום מקרים שבהם תאוצה נוצרת שלא בעקבות כוח. לפי האינטואיציה (וגם לפי הפיזיקה של אריסטו) על כל החפצים שזזים יש מין "תאוצה שלילית קבועה". אם אני אבעט בכדור הוא יתגלגל במהירות מסויימת, ואז יאט וייעצר. אם אני ארה עם תותח לשמיים הפגז יאט ויאט עד שהוא ייפול חזרה למטה. כיום ברור לנו שזה נובע מכוח הכבידה ומכוח החיכוך, אבל באת פרסומם של חוקי התנועה זה לא היה ברור בכלל.

למשה: למעשה כל המתמטיקה כולה (להוציא יוצאי דופן בודדים?? נראה לי שלא), היא טאוטולוגיה. גדולתו של ניוטון הוא שהוא הראה שאם קוראים לדברים בשמות, אפשר ליישם את חוקי המתמטיקה כמעט לגבי כל דבר בעולם הפיזי. אם נגדיר מונחים כמו "כוח" ו"תנע", נוכל לחשב בדיוק רב מה יקרה לעצם שמופעל עליו כוח כזה וכזה. בלנק - שיחה 14:37, 1 בנובמבר 2012 (IST)

בלנק, מהחוק השני נובע שכוח נמצא ביחס ישר לתאוצה, בלי תלות בגורמים נוספים, ולכן החוק הראשון אכן נובע מהשני. כנראה שניוטון ציין אותו כי הוא מספיק חשוב בפני עצמו. ולגבי טאוטולוגיה, יש פה בלבול של משמעות המילה. במתמטיקה, וגם בפיזיקה (כשהאקסיומות הן תוצאות ניסויים), כל האמירות הן טאוטולוגיות. אילו ניוטון היה אומר "אם החוק הראשון נכון החוק הראשון נכון" זו טאוטולוגיה במשמעות הלוגית של המילה ואין איתה שום בעיה. אבל משה טוען שניוטון הגדיל לעשות, והוסיף לומר "לכן החוק הראשון נכון", זו כבר שגיאה לוגית שבטעות השתרשה בשם השגוי "טאוטולוגיה" גם כן. בלנק השתמש במשמעות הראשונה ואילו משה במשמעות השנייה. דניאל • תרמו ערך 19:13, 1 בנובמבר 2012 (IST)

החוק הראשון של ניוטון אינו מקרה פרטי של החוק השני ואינו טאוטולוגיה. החוק הראשון מגדיר מהי מערכת יחוס אינרציאלית, ובכך מגדיר מתי שני החוקים האחרים תקפים. קל לראות שהם אינם תקפים במערכות לא אינרציאליות. בבתי הספר וגם ברוב השיעורים באוניברסיטה לא מסבירים זאת היטב, ולכן נוצר הרושם שהחוק הראשון מיותר. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אם תשים לב, זה מאוד דומה למה שכתבתי. הבעיה היא שבבתי הספר מלמדים בדיוק מה שניוטון כתב. לפחות כך בתרגום לאנגלית של ספרו. משה פרידמן - שיחה 23:28, 1 בנובמבר 2012 (IST)

Every body perferves in its state of rest, or uniform motion in a right line, unless it is compelled to change that state by forces impres'd thereon. (מתוך התרגום לספרו משנת 1729). משה פרידמן - שיחה 00:06, 2 בנובמבר 2012 (IST)

כמעט פילוסופיה, פיזיקה

איך הטבע יודע להתנהג לפלי המתמטיקה שאנחנו כתבנו? חלקיק לא באמת עושה חשבון ווריאציות ומחליט לנוע על המסלול בו הפעולה מינימלית. חלקיק לא שמע על זה שההסתברות למצוא אותו היא פונקציית גל בריבוע. האם ניתן להבין מכך שישנו "כוח עליון" שעושה את החישוב ומחליט בשביל החלקיקים איך התנהג? 192.114.105.254 10:38, 1 בנובמבר 2012 (IST)

זה הפוך כמובן. אנחנו מסתכלים על התנהגות החלקיקים ואז ממציאים מודלים מתמטיים שמתאימים להם. ברטראנד ראסל אמר פעם ש"העובדה ש-3 ועוד 3 תמיד שווים ל-6 אינה מדהימה יותר מהעובדה ששלוש רגל תמיד יהיו שווים ליארד אחד"-הכל תלוי רק בהגדרה שלך למספרים, מונחים, ואירועים. מה שנכון הוא שאכן קיימים "חוקי טבע", שהטבע מציית להם תמיד. רוצה לקרוא לזה "כוח עליון?" לך על זה. בלנק - שיחה 16:49, 1 בנובמבר 2012 (IST)

אני סבור אחרת. המתמטיקה לטעמי היא שפה אנושית, שמקורה בתודעה שלנו ולא בנסיון הנרכש. במיוחד המתמטיקה היותר מתקדמת. (ישנן דעות נוספות בנושא זה). בכל זאת, אנו מוצאים שניתן לתאר את כל חוקי הטבע המוכרים לנו בעזרת שפה זו. אין כל סיבה אפריורי שחוקי הפיסיקה יצייתו לשפה אנושית, אם אכן היא לא נרכשת. למיטב זכרוני קאנט דן בבעיה זו וטען כי אכן הטבע איננו מציית לחוקי המתמטיקה, אבל התודעה שלנו מצייתת להם. היכולת שלנו לקלוט ולארגן ידע מוגבלת לחוקי הלוגיקה והמתמטיקה, ולכן איננו מסוגלים לדעת שום דבר מחוץ לזה. לכן, התמונה של המציאות שנמצאת אצלנו בתודעה מצייתת לחוקי הטבע, אולם אין שום אינדקציה שיש טבע כזה מחוץ לתודעה שלנו. אפשר להמשיל זאת למחשב מאוד משוכלל, שיש לו בינה מלאכותית, והוא מסוגל להתנהל בצורה מאוד מורכבת מול העולם שמחוצה לו. יום אחד הוא עשוי לתהות לעצמו איך שזה שכל המציאות מכילה רק 0 ו-1, ומצייתת למספר מאוד מסויים של פעולות לוגיות. האמת היא, כמובן, שזו פשוט השפה שממנה מורכבת התודעה שלו, ואין בין תפיסת המציאות שלו למציאות החיצונית הרבה מן המשותף. משה פרידמן - שיחה 21:24, 3 בנובמבר 2012 (IST)

מעולם לא הודגם אספקט של המציאות שאינו ניתן לתאור על ידי פעולות לוגיות פשוטות על 0 ו-1. דניאל • תרמו ערך 21:28, 3 בנובמבר 2012 (IST)

אז? משה פרידמן - שיחה 21:43, 3 בנובמבר 2012 (IST)

במשל שלך המחשב לא תופס את המציאות טוב כמונו. לדעתי הוא תופם אותה באותה מידה של הצלחה. דניאל • תרמו ערך 21:57, 3 בנובמבר 2012 (IST)

ייתכן, אבל זה משל שבא להמחיש רעיון, לכן אין טעם להתווכח על נכונות המשל. מה שחשוב זה לא האיכות של השפה, אלא הטענה העקרונית שיכולת התפיסה של התודעה מוגבלת לשפה שלה. משה פרידמן - שיחה 22:07, 3 בנובמבר 2012 (IST)

אני מצטער, רק עכשיו קלטתי שתגובתי למעלה בכלל לא קשורה לשאלה של השואל המקורי. לשאלה המקורית, ראה התייחסות מפורטת בספרו של יובל שטייניץ "טיל לוגי מדעי וכו'". משה פרידמן - שיחה 22:19, 3 בנובמבר 2012 (IST)

כמה חומץ+סודה לאפייה = 950 ליטר פד"ח?

עברו הרבה יותר מדי שנים, וגיליתי ששכחתי איך מחשבים דברים כאלה. חומץ 5%, סודה ביקרבונט. תודה לפותר/ת מראש. הפיקנופודיה טובה ממך! אילן שמעוני, - שיחה 15:44, 1 בנובמבר 2012 (IST)

טלסקופ חלל

האם יש השפעה למהירות הסיבוב של טלסקופ סביב כדור הארץ על המדידות? אני מדבר על כל מיני הסחות כמו הסחה גרביטציונית או הסחה לאדום. נניח שאני רוצה למדוד את האורך גל של חלקיק שמגיע מכוכב מרחק. 109.65.192.97 21:29, 1 בנובמבר 2012 (IST)

המוח צורך יותר דם בשעת חשיבה או למידה?

זכורני שלמדתי פעם שהמוח צורך יותר דם בשעת חשיבה או למידה בדומה לצורך הריאות בזמן פעילות ספורט, יש מקור לדבר זה? ושאלה נוספת, האם ידוע לכם על תיאוריה בעבר שבה נטען שחוף הגוף עולה (במדת מה) כאשר לומדים בצוותא באופן פעיל של משא ומתן? (נשמע משהו מהפילוסופיה היוונית). מוטיבציה - שיחה 00:34, 2 בנובמבר 2012 (IST)

כל איבר בגוף צורך יותר חמצן (שמגיע בדם) בזמן מאמץ. זה נכון לקיבה בעת עיכול, לשרירים בעת ריצה ולמוח בעת למידה. דניאל • תרמו ערך 22:23, 2 בנובמבר 2012 (IST)

ואני אוסיף, שבמדעי המוח (ראה בערך) משתמשים בזה, כשעושים דימות תהודה מגנטית תפקודי (fMRI). eman • שיחה • ♥ 02:53, 3 בנובמבר 2012 (IST)

דניאל, כפי שכתבתי למדתי את זה פעם, אך ניסיתי לחפש היכן זה כתוב בויקיפדיה (שהמוח צורך יותר דם בשעת לימוד) ולא מצאתי. ובאותו הקשר יש לי שתי שאלות: האם זה מוכח באמת שהמוח מתאמץ יותר בשעת לימוד? ושאלה נוספת, האם כשאנו אומרים שאיבר מסויים (כמו השריר או המוח או הריאות) צורך יותר דם פירושו של דבר שלחץ הדם באותו איבר גדל (עולה)?מוטיבציה - שיחה 18:48, 3 בנובמבר 2012 (IST)

לחץ הדם אמור להיות קבוע בכל הגוף, ללא תלות באיבר שאתה מודד. בלנק - שיחה 20:01, 3 בנובמבר 2012 (IST)

אז במה מתבטא השינוי בשאר האיברים כשהמוח למשל נוטל מנת דם מכובדת בשעת למידה 'על חשבון' הריאות או מערכת העיכול, או כאשר מערכת העיכול משתמשת יותר בדם על חשבון המוח והאחרים? מוטיבציה - שיחה 22:12, 3 בנובמבר 2012 (IST)

כלי דם מתכווצים או מתרחבים בהתאם לצורך. יוסי • שיחה 08:51, 4 בנובמבר 2012 (IST)

לחץ הדם לא קבוע בכל הגוף. הוא תלוי מאד בגובה היחסי של החלק בגוף. אצל אדם עומד, לחץ הדם ברגליים גבוה מבראש. בעת עמידת ראש המצב 'מתהפך'. לחץ הדם שמודדים, מוגדר כלחץ הדם שבגובה הלב. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

מונחים בכימיה

שמתי לב שבטכניון בפקולטה לכימיה במקום "ניסוי" אומרים "ניסיון". למה? 109.65.219.216 11:20, 2 בנובמבר 2012 (IST)

בדיוק לאחרונה קראתי את ספריו של יצחק לבנון "על כל שאלה תשובה" (משנת 1959), ושמתי לב שלאורך ספריו הוא משתמש במונח "נסיון" (ונסיונות) במקום ניסוי וניסויים שאנו רגילים לומר. אם זה נכון ועקבי מה שאמרת לגבי הטכניון (לי באופן אישי אין מידע על הטכניון - ואני מסתמך על דבריך בלבד) כנראה מדובר בצורת מינוח ישנה שהטכניון הותיק עדיין משמר. מוטיבציה - שיחה 18:40, 3 בנובמבר 2012 (IST)

}}

פיזיקה הוואקום

האם זה נכון שקיים נושא מחקר בשם "פיזיקת הוואקום"? 109.65.219.216 20:02, 2 בנובמבר 2012 (IST)

כן. ראה כאן. בלנק - שיחה 21:17, 2 בנובמבר 2012 (IST)

מציאת גבול בעזרת לופיטל

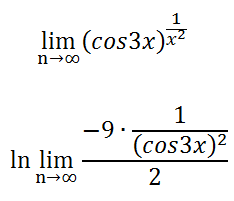
עליי למצוא את הגבול הראשון. על מנת לפתור התכוונתי למצוא מכפלת הגבול ב-ln. והגעתי לגבול השני. בתשובה המפורטת ראיתי, שכל הגבול הזה שואף ל-(9/2-). משמע, הביטוי עם הקוסינוס שואף לאחד כש-X שואף לאינסוף. לא הבנתי למה, הרי הקוסינוס בריבוע נע בין 0 ל-1, אז איך ניתן להגיד שהוא שואף ל-1? תודה, אביעד‏ • שיחה 11:41, 3 בנובמבר 2012 (IST)

טוב, הבנתי את הטעות המטופשת. זה שואף ל-0 ולא לאינסוף. אביעד‏ • שיחה 11:44, 3 בנובמבר 2012 (IST)

וזה x ולא n ... eman • שיחה • ♥ 12:51, 3 בנובמבר 2012 (IST)

תחושת תאוצה וסיבוב

בגוף אדם ישנם גלאים לסיבוב ותאוצה, נכון? לדוגמה אני יכול עם עיניים עצומות לדעת שאני מסתובב. לגבי תאוצה אני קצת לא בטוח- יתכן שמה שאני מרגיש זה כוח נורמלי כלומר אני משתמש במישוש לצורך גילוי התאוצה(תקנו אותי אם אני טועה!).

אז אני שואל- איך פיזית בנויים הגלאים האלא. שמעתי (ממש מזמן ואולי בטעות) שיש איזה מיכל עם נוזל בראש המאתר סיבוב בגלל חיכוך פנימי (וזה מסביר למה יש סחרחורת אחרי כמה סיבובים לאותו כיוון). תפנו אותי לשמות של האיברים המשמשים בגלאי תנועה. Corvus,(שיחה) 12:24, 3 בנובמבר 2012 (IST)

ראה מערכת שיווי המשקל. eman • שיחה • ♥ 12:50, 3 בנובמבר 2012 (IST)

מהלך חופשי ממוצע

אני רוצה למצוא מהלך חופשי ממוצע של גז חנקן. נעזר בוולפראם אלפה. מצד אחד הוא נותן לי את זה ומצד שני כאן. לא מדובר בעיית דיוק, יש פה הבדל של סדר גודל (פי 10). את הנתון לגבי קוטר מולקולת חנקן לקחתי מויקיפדיה. אז אחד החישובים שגוי. איזה מהם ולמה? 79.182.246.53 13:11, 3 בנובמבר 2012 (IST)

קו ישר בין שתי נקודות אינו המרחק הקצר ביותר?

קראתי שלהשיט אוניה בנתיב קשתי זה חוסך דרך ארוכה יותר של הפלגה בנתיב ישר בין שתי נקודות(!), האם זה נכון, וא"כ כיצד יתכן דבר כזה? (כלומר ביבשה המרחק בין שתי נקודות הוא בודאי הכי קצר, אז מדוע בים להפך?) מוטיבציה - שיחה 18:54, 3 בנובמבר 2012 (IST)

זה לא קשור לים או יבשה. זה נובע מפני שאנחנו על פני כדור. ועל פני כדור אין קווים ישרים בכלל. יש רק קשתות (או קווים מסובכים יותר). הקו המחבר בין שתי נקודות במרחק הקצר ביורת הוא קשת גאודזית. כשמסתכלים על מרחקים קצרים, הקשת הזו קרובה לקו ישר. אבל אם אתה מדבר על מרחקים בין ארצות או יבשות, אז החריגה מקו ישר כבר ניכרת.

ובוודאי אין טעם לעשות קו ישר על המפה, כי מפה היא רק היטל שיוצר עיוות.

eman • שיחה • ♥ 19:01, 3 בנובמבר 2012 (IST)

טוב, למרות מאמציי הצלחתי להבין רק מעט מדבריך. אז אעתיק לפניך את הכתוב: "האם קו ישר הוא תמיד המרחק הקצר ביותר בין שתי נקודות? תשובה: קו ישר אינו תמיד המרחק הקצר ביותר בין שתי נקודות. הספנים חוסכים דרך ארוכה בהשיטם את האניות בנתיב קשתי." זה הציטוט מהספר "על כל שאלה תשובה" של יצחק לבנון. אם זה נכון שאין כאן קו ישר בכלל, אז השאלה מעיקרה לא רלוונטית וחסרת משמעות, לא כי?! מוטיבציה - שיחה 20:37, 3 בנובמבר 2012 (IST)

כיצד תגדיר קו ישר? ההגדרה הסטנדרטית לקו ישר היא הקו הקצר ביותר בין שתי נקודות אז השאלה שלך חסרת משמעות. מה שיצחק לבנון התכוון אליו הוא שקווים ישרים במפה אינם באמת קווים ישרים בכדור הארץ. זאת משום שמפה היא היטל שטוח של פני כדור הארץ הכדוריים, ולכן היא מעוותת מרחקים. למשל שים לב שכל הקו העליון במפת העולם הוא למעשה כולו נקודה אחת! הקוטב הצפוני. להסבר רחב יותר ראה בערך מעגל גדול. דניאל • תרמו ערך 21:18, 3 בנובמבר 2012 (IST)

ראשית כל הרשה לי להודות לך על הבאת הקישור במקומו. ושנית, יכול להיות שיצחק לבנון התכוון לדבריך, אבל המציאות היא שליד השאלה והתשובה הוא הדפיס איור של כדור המקשה את ההסבר עוד יותר לכאורה. לנוחיותך העליתי את לרשת את הקטע המדובר. צבעתי באדום את הנתיב הקשתי, ובירוק את הנתיב הישר. אני מקווה שמתוך זה תבין את הקושי שלי בהבנת הנושא. מוטיבציה - שיחה 22:03, 3 בנובמבר 2012 (IST)

צבעת באדום קו רוחב, זה לא הנתיב הישר, אלא הנתיב המתחזה לישר בהיטל הסטנדרטי. הנתיב הישר מסומן בשחור והוא עובר קצת צפונה לקו הירוק. הקו הירוק שסימנת אינו ישר כלל. הוא ישר כקו על הציור השטוח של כדור הארץ אבל זו אשליה שנגמרת בשל ההיטל (שבמקרה הז אינו סטנדרטי). אם "תנפח" את האיור למרחב התלת ממדי העין תבחין מיד בכך שהקו השחור הוא הישר. דניאל • תרמו ערך 22:10, 3 בנובמבר 2012 (IST)

כעת אני מבין את הדברים, תודה. ותוך כדי כך תמה על 'חידושו' של לבנון, וחושב ששאלתו מעיקרה אינה נכונה לכאורה כי אם 'ננפח' (כפי דבריך) את האיור למרחב התלת ממדי, נגלה שכן מדובר במרחק בין שתי נקודות (גם אם מדובר בצורה קשתית), הרי לא ייתכן, לפי מיטב ידיעתי, לקדוח מנהרה דרך הגרעין מישראל לאוסטרליה למשל. הקו הישר בכדור הארץ הוא ביטוי לשתי נקודות על המעטפת החיצונית של כדור הארץ. מוטיבציה - שיחה 22:19, 3 בנובמבר 2012 (IST)

לבנון השתמש במינוח לא מוצלח. במקום קו ישר היה עליו לומר קו רוחב. הרעיון אינו אינטואיטיבי לרבים. כשמוסלמי בקנדה רוצה להתפלל לכיוון מכה הוא צריך לפנות צפונה ולא מזרחה כפי שהרוב יסברו. דניאל • תרמו ערך 22:46, 3 בנובמבר 2012 (IST)

על מפה כזו, קו ישר מסמן גם את המרחק הקצר ביותר, כך שההכללות לעיל אינן נכונות. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

נכון, דיברתי על ההטלות הפופולריות יותר. אבל לפי Theorema Egregium, לכל היטל יהיה עיוות כלשהו. דניאל • תרמו ערך 09:50, 4 בנובמבר 2012 (IST)

מהי כוס כימית?

קראתי בערך כוס כימית, שכוס כימית עשויה בד"כ מזכוכית, א"כ אני מתפלא איך מחממים אותה עם להבת אש במעבדות בלא שהיא תתפוצץ? לפי מיטב ידיעתי אם דבר כזה היה נעשה עם כוס או ספל זכוכית של קפה הוא היה מתפוצץ. אז במה שונה כוס כימית משאר הכוסות מזכוכית? (קראתי בערך כוס כימית שלפעמים הן מיוצרות מפלסטיק!) מוטיבציה - שיחה 22:36, 3 בנובמבר 2012 (IST)

אין לי נסיון עם כוסות כימיות. הסיבה שכוס זכוכית נשברת בחימום היא בגלל שהטפמרטורה בתוכה לא אחידה, וזה גורם להתפשטות תרמית לא אחידה, למאמצים ולבסוף לשבירה. אם תחמם את הכוס באיטיות רבה היא לא תשבר. ככל שהכוס דקה יותר, ובעלת צורה פשוטה, היא תהיה עמידה יותר בחימום, כי כך לא נוצרים הפרשי טמפרטורה חדים בתוך הכוס. מוכרים כוסות זכוכית דקות עבור משקאות חמים. לגבי פלסטיק: יש המון סוגים של פלסטיק שניחנים בסגולות שונות. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

את העיקר שכחתי: יש סוגים של זכוכית שלהם מקדם התפשטות תרמית קטן, ולכן הפרשי טמפרטורה חדים בפנים לא יביאו לשבירה. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

ככתוב בערך כוס כימית עשויה לרוב מזכוכית בורוסיליקט המוכרת גם בשם פיירקס, תמצא כלי בישול ואפיה מזכוכית זו גם במטבחך. שנילי - שיחה 10:09, 4 בנובמבר 2012 (IST)

תודה על התשובות. אגב, במטבחי אין כלי בישול או אפייה מזכוכית. אנחנו משפחה פשוטה. חוץ מזה, אם היה כאלה בביתי (או אם הייתי מודע לקיומם של כלים כאלה) לא הייתי צריך להגיע רחוק לכוס כימית ולמעבדה. מוטיבציה - שיחה 22:00, 6 בנובמבר 2012 (IST)

אם אתה או הוריך בגיל המתאים אני די משוכנע שקיבלתם כלי פיירקס לחתונה. שנילי - שיחה 22:02, 10 בנובמבר 2012 (IST)

ראיתי בדף המשתמש שאתה ממשפחה חרדית ספרדית אזי דע לך, מבלי שאפסוק הלכה, שבמחלוקת האם כלי זכוכית בולע או לא ובעיקר שהוא חם, הפוסקים הספרדים פוסקים שהוא אינו בולע ולכן כלי פיירקס שימושי בהיותו ניתן להגעלה. שנילי - שיחה 22:24, 10 בנובמבר 2012 (IST)

נגזרות

נתון $x^{2}+y^{2}=t^{2}$ וגם $x\sin t=ye^{y}$. איך אני מוצא את הנגזרות החלקיות $\partial x/\partial t;\partial y/\partial t$? 192.114.105.254 15:21, 5 בנובמבר 2012 (IST)

כאשר מדובר בפונקציה סתומה מוגדרת, אתה יכול לגזור ישירות את איברי הביטוי ולחלץ את הנגזרת הרצויה (למשל במקרה הראשון צריך לפתור את המשוואה הדיפרנציאלית: $2x+2yy'=0$). דניאל • תרמו ערך 11:39, 6 בנובמבר 2012 (IST)

דווקא בשתי הדוגמאות האלו עדיף בהרבה לחלץ את המשתנה שאותו גוזרים, ואז פשוט לגזור נגזרת חלקית. ‏Setreset • שיחה 13:13, 6 בנובמבר 2012 (IST)

הצגה פרמטרית

תנועה של חלקים מתוארת ע"י: y=Asin(t)*e^-(at) ו-y=cos(t)*e^-(at). כאשר a,A קבועים. כדי להבין את המסלול, אם t מתחיל מ-0, הצבתי אפס, והשאפתי את הפונקציות לאינסוף. ברור לי שבאינסוף שתי הפונקציות שואפות ל-0, ולכן תנועת המסלול שואפת לראשית הצירים. אך איני מבין דבר מה. כאשר אני מגדיל את t, בעוד הביטוי המעריכי קטן בערכו, פונקציות הסינוס והקוסינוס נעות בטווח שבין 1 למינוס 1, כלומר עוברות בין השליליות והחיוביות, ולכן אני מתקשה לצייר את תנועה החלקיק. תודה, אביעד‏ • שיחה 15:23, 5 בנובמבר 2012 (IST)

נכון שהפונקציות הטריגונומטריות כל הזמן נעות בין -1 ל-1, אבל האקספוננט שואף לאפס (והוא שואף לאפס מהר מאוד), והתוצאה של הכפלת משהו ששואף לאפס במשהו שמתנדנד בין -1 ל-1 (או בין a ל-a-) הולכת ומתקרבת לאפס. ראה לדוגמה כאן. 16:26, 5 בנובמבר 2012 (IST)

אני מבין שבגלל שהאקספוננט שואף לאפס מהר מאוד הפונק מתקרבת ל-0 כולה, אך כיצד זה יכול להיות שעד שהיא מתקרבת היא אינה נעה בין חיוביות לשליליות? כיצד נראית ההצגה הפרמטרית? אביעד‏ • שיחה 16:39, 5 בנובמבר 2012 (IST)

אתה מתכוון במקרה ש- x=cos(t)*e^-(at)? ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 18:44, 5 בנובמבר 2012 (IST)

כן. אביעד‏ • שיחה 19:47, 5 בנובמבר 2012 (IST)

מדובר בהצגה פרמטרית של ספירלה מתכנסת. תחשוב שניה על קואורדינטות רדיאליות, כאשר t מציין את הזווית של מעגל היחידה ו- Ae^-(at) מציין את הרדיוס. כאשר שנייהם תלויים באותו פרמטר t. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 20:45, 5 בנובמבר 2012 (IST)

נכון, אבל הבט נא כאן. בתחום ש-x גדול מ-0, יש מין חצי מעגל. עכשיו, ברור לי מדובר שחלק מתנועה ספירלית אולם איני מבין איך יכול להיות שאין מעבר משליליות לחיוביות לקראת 0. אביעד‏ • שיחה 22:15, 5 בנובמבר 2012 (IST)

מה שאתה מציג שם אינה הצגה פרמטרית אלא פשוט הצגה של שתי פונקציות על גבי אותו גרף. אם מעניין אותך מה שאתה מציג אז אלו בעצם פונקציות סינוסואידליות כאשר הן מתכנסות לאפס תחת מעטפת אקספוננציאלית. כאשר הפונקציה מתקרבת לאפס היא אכן תונדת בין חיובי לשלילי, במה שהצגת האקספוננט מתכנס מהר, תנסה מקדם קטן (נניח 0.05) לאקספוננט ותראה שהפונקציה תונדת.

הצגה פרמטרית שאני מניח שבמקור התכוונת היא בעצם גרף של נקודות כאשר ערכי x שלהן מבוטאים ע"י Acos(t)*e^-(at) ואילו ערכי y שלהן מבוטאים ע"י Asin(t)*e(-at) כאשר עבור כל t ישנה נקודה. הצגה פרמטרית פשוטה עם קוסינוס וסינוס נותנת את מעגל היחידה, הכפלה שלהם באקספוננט שלילי יוצרת ספירלה מתכננת עבור ערכי t חיוביים.

ראה כאן הצגה פרמטרית של הגרף. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 22:59, 5 בנובמבר 2012 (IST)

שים לב שבלינק ששלחתי יש למטה גם הצגה פרמטרית. שם אין מעבר בין שליליות לחיוביות. אביעד‏ • שיחה 06:34, 6 בנובמבר 2012 (IST)

תודה על ההצגה הפרמטרית. אבל אם זה טוב עבור 0.05t, מדוע זה לא שמתקבל גם עבור t?

זה כן, פשוט זה מתכנס מהר ואתה לא רואה את זה. אם היה אפשר לעשות זום היית רואה גם עבור t. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 00:04, 7 בנובמבר 2012 (IST)

קרח מתפוצץ

שמתי לב לתופעה מעניינת. כשאני מוזג מים מהברז לכוס עם קוביית קרח, אז קוביית קרח נסדקת ועושה רעש קל של נפיצה. היום איזו קוביה ממש "התפוצצה" לי בכוס לשני חתיכות. למה זה קורה? 109.64.250.205 22:34, 5 בנובמבר 2012 (IST)

אתה מוזג מים רותחים או חמים מאוד? לי התופעה מוכרת רק כאשר שמים קרח בתה או קפה כדי ליצור תה או קפה קרים. אני מניח שאז זה קורה כי הקוביה מתחילה להתמוסס, ויש הבדלי לחצים וכאלה. (זה בטח קשור גם לאנומליה של המים) בלנק - שיחה 23:13, 5 בנובמבר 2012 (IST)

התופעה קורית גם כשמוזגים מי ברז. זה קורה בגלל הלם תרמי (Thermal shock, איזו בושה שטרם נכתב הערך, אני אנסה להגיע לזה בקרוב). בקצרה, זה קורה בגלל שהצד החיצוני של הקרח מתחמם מהר מאוד ומתכווץ, והצד הפנימי נשאר כפי שהיה, וזה גורם למאמצים בתוך החומר (הקרח). כשהמאמצים יותר גדולים מהחוזק של החומר, הוא נשבר. ‏Setreset • שיחה 13:20, 6 בנובמבר 2012 (IST)

שאלה במד"ר

איך פותרים $(x-{{e}^{y}}){\frac {dy}{dx}}+1=0$? 109.64.250.205 23:01, 5 בנובמבר 2012 (IST)

מספר שאלות על חום ואנרגיה

שלום, יש לי מספר שאלות בנושא של חום ואנרגיה, אשמח לדעת מהן התשובות...

1. קראתי ש"חום הוא תנועה של חלקיקי חומר- אנרגיה", האם תנועה של חלקיקי חומר נקראת אנרגיה או מה שמפעיל את התנועה נקרא אנרגיה?

2. קראתי בנוסף, שכאשר מקרבים גוף שחלקיקיו נעים במהירות (גוף חם) אל גוף שחלקיקיו נעים באיטיות, פוגעים החלקים המהירים בחלקים האיטיים, וזה גורם לחלקיקים המואצים להיות איטיים. כל המהלך הזה נגרם כתוצאה מ"תכונת האיזון בטבע". שאלותי בעניין זה הן שאלות הבנה: (א) קודם כל איך יתכן שכאשר אני לוקח כוס עם תה ומצמיד לה כוס עם מים קרים, החלקיקים עוברים דרך הזכוכית?! (ב)דבר שני, מדוע החלקים המהירים פוגעים בחלקים האיטיים ולא להפך, הרי זה הדדי! (ג) מה גם שאני תמה מדוע החלקיקים המואצים לא גורמים לחלקיקים האיטיים להיות מואצים, אלא הכל קורה להפך האיטיים מאיטים את המואצים. (ד) לצערי, איני מבין מה זה "תכונת האיזון בטבע"- אוכל לקבל הסבר בבקשה?. מוטיבציה - שיחה 18:36, 6 בנובמבר 2012 (IST)

1. אני לא חושב שיש הבנה מלאה מה זה אנרגיה, אבל בהקשר הזה נראה לי מספיק לומר שאנרגיה היא תכונה של חלקיקים בתנועה.

2. מבחינת השימוש במושגים יש כאן בלבול מסויים. כשאתה אומר "חום" אתה מתכוון לומר, בשפה המדעית, טמפרטורה. המושג "חום" פירושו מעבר של אנרגיה.

3. כאשר מצמידים חומר בעל טמפרטורה גבוהה לחומר בעל טמפרטורה נמוכה, החלקיקים המהירים מתנגשים באיטיים, וזה גורם לחלוקה של האנרגיה בין החומרים. אתה יכול לחשוב על כדור ביליארד מהיר שמתנגש בכדור איטי, התוצאה היא שהכדור האיטי מתחיל לנוע (מקבל אנרגיה), על חשבון הכדור המהיר שמאבד מהירות (ולכן מאבד אנרגיה). עכשיו תכפיל את זה בהמון חלקיקים. התהליך הזה, באופן מצטבר, גורם לחימום (=העברת אנרגיה) של החומר בעל הטמפרטורה הנמוכה, על חשבון החומר בעל הטמפרטורה הגבוהה.

4.החלקיקים לא עוברים דרך הזכוכית. התה מחמם את הזכוכית, והזכוכית מחממת את המים. משה פרידמן - שיחה 20:47, 6 בנובמבר 2012 (IST)

תודה משה,

1. האם לא יודעים בזמננו מה זה אנרגיה, (זה מפתיע אותי, בפרט שזה נאמר ע"י דוקטורנט לפיסיקה), אז איך מדברים על משהו שלא יודעים מהו?

2. האם ניתן לומר שטמפרטורה = אנרגיה? (או שיש צורך להשתמש במילים "מעבר של")

4. אז אתה מסכים עם הטענה ש"כאשר מקרבים גוף שחלקיקיו נעים במהירות (גוף חם) אל גוף שחלקיקיו נעים באיטיות, פוגעים החלקיקים המהירים בחלקיקים האיטיים"?

5. מה זה "תכונת האיזון בטבע"? יש מונח כזה או ערך בויקיפדיה שאני יכול לקרוא על זה או שזו המצאת מונח על ידי מורה? (אולי הכוונה להומואסטזיס?!)מוטיבציה - שיחה 21:14, 6 בנובמבר 2012 (IST)

1. קודם כל, אני לא בטוח שכולם יסכימו איתי. בכל אופן, הפיסיקה מתארת תופעות, ומושג האנרגיה הוא גורם מרכזי מאוד בתיאור התופעות שאנו רואים. השאלה "מה זה אנרגיה", במידה ויש לה משמעות, איננה הכרחית על מנת להשתמש במושג הזה. הדבר איננו ייחודי למושג האנרגיה, והוא תקף, לדעתי, לרוב המושגים היסודיים בפיסיקה.

2. לא. טמפרטורה זו תכונה של חומר, שתלויה באנרגיה הפנימית שלו. אין זהות בין המושגים, אבל יש קשר ביניהם.

4. זה גם נכון. כמובן שמבחינה פיסקלית זה שקול לחלוטין לאמירה שהחלקיקים האיטיים פוגעים במהירים. ישנם דרכים נוספות למעבר חום בין גופים.

5. מעולם לא שמעתי את הביטוי הזה. אני יכול לנסות לנחש מה הוא אומר, אבל עדיף לשאול את מי שכתב אותו. משה פרידמן - שיחה 22:15, 6 בנובמבר 2012 (IST)

1. המטרה במדע היא לתת לכל דבר הסבר במונחים של מושגים קודמים אבל איפשהו השרשרת צריכה להיעצר ויש לבחור מונחי בסיס אקסיומתיים. אנרגיה זה מקום טוב לעצור. זה לא אומר שאין הבנה איזה תפקיד האנרגיה משחקת בעולמנו ואיך להשתמש במושג כדי לנתח את עולמנו, אבל להסביר אנרגיה באמצעות מונחים אחרים רק יוביל לעוד מונחים לא מוגדרים או להגדרה מעגלית. דניאל • תרמו ערך 00:17, 7 בנובמבר 2012 (IST)

אפשר לבסס את מושג האנרגיה על מושג הזמן. האנרגיה היא הגודל השמור, כאשר חוקי הפיזיקה קבועים בזמן. לדעתי שם המקום הטוב לעצור. "תכונת האיזון בטבע" נשמע לי כמו כינוי גרוע לכללי שיווי משקל תרמודינמיים שונים. כדי להבין את ההבדל בין אנרגיה וטמפרטורה, מומלץ ללמוד את המושג קיבול חום. ותיקון: חום איננו רק מעבר של אנרגיה, אלא מעבר של אנרגיה שאיננו עבודה. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אני אומר את האמת, למרות התאמצותי בימים האחרונים להבין חלק מהנאמר כאן לא עלה בידי הדבר. השאלה מהי אנרגיה עדיין נותרה בעינה (ראיתי את ההסבר של משה פרידמן שהמשמעות של אנרגיה איננה הכרחית כדי להשתמש בה כמונח, וזה מאוד קשה לי להבנה). בכל אופן תודה לכל מי שסייע בפתרון הבעיה עד עתה. מוטיבציה - שיחה 22:57, 8 בנובמבר 2012 (IST)

אלמט אורך

אני "חוקר" תנועה של חלקיק על פני גליל. רשום במקום מסויים מסיבות לא ברורות שאלמט אורך של המסלול הוא $dl={\sqrt {R^{2}d\theta ^{2}+dz^{2}}}$. אתם יכולים להסביר לי מאיפה אני מגיע לזה? עשיתי פרמטריזציה לגליל, לא עוזר. אני רואה שזה מזכיר פיתגורס, אני רואה שהנוסחה די הגיונית מבחינת אינטואיציה. אבל לא מבין איך מגיעים לזה.

איך לדוגמה הייתי עושה אם המסלול היה על פני חרוט ולא גליל? 109.64.250.205 21:40, 6 בנובמבר 2012 (IST)

ראה קואורדינטות גליליות#תכונות מטריות. אם תחשב את אורך האלמנט ותציב dr=0 תקבל בשדיוק את מה שכתבת. ‏Setreset • שיחה 14:33, 8 בנובמבר 2012 (IST)

קוונטים, הטלה

השאלה פה. התשובה לא ברורה לי. קל להוכיח ש$P=P^{2}$. אבל לא יודע איך לכתוב את P בבסיס של פולס מינוס. כל מה שהעדי אליו זה$P=(a_{+}|+>+a_{-}|->)(a_{+}^{*}<+|+a_{-}^{*}<-|)=a_{+}a_{+}^{*}|+><+|+a_{+}a_{-}^{*}|+><-|+a_{-}a_{+}^{*}|-><+|+a_{-}a_{-}^{*}|-><-|$.

זה מתרב איכשהו לתשובה? יש איזושהי דרך לכתוב את זה "בבסיס של |+_>" או שאולי מה שעיתי זו התשובה הסופית ואין דרך להתקדם מכאן? 109.65.193.226 20:28, 7 בנובמבר 2012 (IST)

כל מה שאתה צריך לעשות הוא לכתוב את המקדמים שמצאת בצורת מטריצה. ירון ק. - שיחה 07:41, 9 בנובמבר 2012 (IST)

מכפלה טנזורית

הערך נורא קשה להבנה למי שאין לו רקע. איך אני עושה לדוגמה את $\left({\begin{array}{c}1\\0\end{array}}\right)\otimes \left({\begin{array}{cc}0&1\end{array}}\right)$ או $\left({\begin{array}{c}1\\0\end{array}}\right)\otimes \left({\begin{array}{cc}1&0\end{array}}\right)$? 109.65.193.226 20:51, 7 בנובמבר 2012 (IST)

$\left({\begin{array}{c}a\\b\end{array}}\right)\otimes \left({\begin{array}{cc}c&d\end{array}}\right)=\left({\begin{array}{cc}ac&ad\\bc&bd\end{array}}\right)$. עוזי ו. - שיחה 01:13, 8 בנובמבר 2012 (IST)

תבורך. 79.182.225.2 17:08, 8 בנובמבר 2012 (IST)

תאוצה משיקית

שלום. אשמח לעזרה. אני צריך להראות שהתאוצה המשיקית שווה לביטוי זה. מה שאני לא מבין הוא למה איני יכול להסתפק בנגזרת של המהירות המשיקית? איך עושים את זה? תודה, אביעד‏ • שיחה 23:10, 7 בנובמבר 2012 (IST)

על פי הנוסחה לחישוב מהירות בקואורדינטות פולריות, אני מבין שזוהי הנגזרת כמובן, אבל לפי הבנתי המהירות הזו אינה דווקא המשיקית, כי אם הכוללת, אז מדוע זוהי המהירות המשיקית, ונגזרתה, התאוצה המשיקית? אביעד‏ • שיחה 00:00, 8 בנובמבר 2012 (IST)

אני חושב שה"תאוצה המשיקית" שמחושבת כאן היא המשיקה למסלול של העצם. כלומר השינוי בערך המוחלט של המהירות. ואז מובן שהביטוי נכתב כך. ‏Setreset • שיחה 14:37, 8 בנובמבר 2012 (IST)

נגזרת בזמן

כשרושמים נקודה מעל קואורדינטה מסוימת מתכוונים לנגזרת מלאה או חלקית בזמן? 192.114.105.254 13:08, 8 בנובמבר 2012 (IST)

נגזרת מלאה, בדיוק כמו במקרה של סימון ע"י תג, עבור גזירה לפי קואורדינטות מרחביות. נגזרת חלקית מסמנים בעזרת כתב-תחתי (עיין כאן) או באמצעות אות מיוחדת. ראה את שתי האפשרויות בערך נגזרת חלקית. בנצי - שיחה 14:19, 8 בנובמבר 2012 (IST)

מאות מליוני מעלות צלזיוס...

קראתי בספר "מה חדש במדע" עמוד 106, על "החום שנוצר בפיצוץ מימני יהיה עצום ויגיע עד כדי עשרות או מאות מליוני מעלות צלזיוס..." מכאן אפשר לראות כי כמעט אין הגבלה למעלות צלזיוס, ואין הגבלה למהירות תנועת האטומים (אנרגיה), האם זה נכון, והאם המספרים הנ"ל מציאותיים? מוטיבציה - שיחה 22:52, 8 בנובמבר 2012 (IST)

לא רואה איך אפשר להגיע מזה למסקנה שאין הגבלה. דניאל • תרמו ערך 23:09, 8 בנובמבר 2012 (IST)

במילים אחרות: יש הגבלה, רק שהיא מאוד מאוד גבוהה- אפילו יותר ממאות מליוני מעלות צלזיוס. בלנק - שיחה 23:40, 8 בנובמבר 2012 (IST)

לומר שאין הגבלה על המהירות זה פשוט לא נכון. יש הגבלה, והיא כמובן מהירות האור. eman • שיחה • ♥ 01:11, 9 בנובמבר 2012 (IST)

אם תשימו לב תראו שנזהרתי בלשוני וכתבתי כי כמעט אין הגבלה... המספר הזה בהחלט נתן לי תחושה כזו, בפרט שלאורך ספר הם משתמשים כמה פעמים במספרים אלה בפשיטות.

אם הגבלת מהירות תנועת החלקיקים (או האטומים?) היא מהירות האור, אז כמה מעלות חום (צלזיוס) יש כאשר חלקיקים של חומר נמצאים בתנועה של מהירות האור- זה ידוע? וכיצד הסיקו שמהירות החלקיקים מגיעה למהירות האור ולא יותר מזה? מוטיבציה - שיחה 07:20, 9 בנובמבר 2012 (IST)

לחלקיק עם מסה במהירות האור יש אנרגיה אינסופית ולכן גם טמפרטורה אינסופית. לגבי המסקנה ראה יחסות פרטית. ירון ק. - שיחה 07:44, 9 בנובמבר 2012 (IST)

אני חושב שהוא מתכוון טכנית: האם ניתן לחמם את החומר למהירות הקרובה למהירות האור. אם כן, איזו טמפרטורה זו תהיה. 79.182.244.104 10:11, 9 בנובמבר 2012 (IST)

נכון, לזה אני מתכוון והגדרת את זה נכון. ("אם ניתן לחמם את החומר למהירות האור, אם כן איזו טמפרטורה תהיה באותו חומר") ואכן, ירון כמדומני לא פתר בעיה זו בתשובתו. אגב, אני עדיין נדהם (באופן החיובי של המילה) מדברי ירון (למיטב הבנתי) שלחלקיק במהירות האור יש אנרגיה אין סופית ולכן טמפרטורה אינסופית. האם יש לזה תקדים מציאותי? מוטיבציה - שיחה 12:48, 9 בנובמבר 2012 (IST)

א. לא. לא תקדים, ולא אפשרות כזו. מהירות האור היא גבול תיאורטי, ולשם האצתם של גופים שמהירותם קרובה למהירות האור למהירויות גבוהות עוד יותר, אפילו בשיעור זעיר ביותר, דרוש כוח עצום ההולך ושואף לאינסוף. כמובן שאין לזה משמעות פיזיקלית. אינסוף הוא כלי טוב להבנת תהליך פיזיקלי ולכיוון שלו, ולאנליזה מתימטית, אבל אין לו ממשות פיזיקלית. נדמה לי שהיבט מאוד דומה עלה באחד הדיונים הקודמים איתך, בו התייחסתי להיבט זה.

ב. ובכל זאת, פטור בלא כלום אי אפשר: הטמפרטורות הגבוהות ביותר קיימות בליבותיהם של כוכבים מאסיביים ביותר, ובהם, קודם: נובות וסופרנובות - סדר גודל של עשרות מיליוני מעלות (מה שטוב בטמפ' כאלה הוא שכבר לא חשוב באיזה סולם משתמשים. ). טמפ' גבוהות עוד יותר קיימות בליבותיהם של כוכבי ניוטרונים. זהו כוכב שכבידתו כה גדולה, עד שחלקיקיו התת-אטומיים קרסו והתנוונו כדי היות ניוטרונים בלבד. השלב הבא הוא המצבים הפיזיקליים השוררים בקרב חורים שחורים, אבל איננו יודעים הרבה על החוקים הפיזיקליים במצבים הקיצוניים המאפיינים גרם שמיים כזה. גם האיסור של פאולי נשבר שם. הכבידה חזקה ממנו. שבת שלום, בנצי - שיחה 13:14, 9 בנובמבר 2012 (IST)

אגב, הטמפרטורה הגבוהה ביותר שהושגה על ידי אדם אפילו גבוהה יותר. בעת יצירת פלזמת קווארקים-גלואונים ב-LHC הגיעו לטמפרטורה מסדר גודל של עשרה מיליון מיליוני מעלות (10¹³). דניאל • תרמו ערך 13:29, 9 בנובמבר 2012 (IST)

לא מדוייק. דבריך נכונים בהשוואה לכוכבים מאסיביים רגילים. המצב המיוחד והמעניין שאתה מציין, קיים בליבותיהם של כוכבי ניוטרונים מאסיביים דיים. בנצי - שיחה 13:48, 9 בנובמבר 2012 (IST)

קודם כל הטענה שאתה מציין היא השערה שלא נתמכת על ידי תצפיות (בשל הקושי בעריכת תצפיות כאלו) ושנית, התייסחתי לטמפרטורה שציין מוטיבציה. לא לטמפרטורה שאתה ציינת. דניאל • תרמו ערך 13:55, 9 בנובמבר 2012 (IST)

בנצי תודה על התשובה המעניינת. (אם כי לאחר שקראתי את תשובת דניאל תמהתי לרגע מדוע הטמפרטורות הנדירות שביותר שהצגת היו בסדר גודל של עשרות מליוני מעלות, וגם מעלות אלה היו בכוכבים הרחוקים מאיתנו שנות אור רבות, בו בזמן שדניאל הציג ניסוי אמפירי בארץ שהאדם עצמו הגיע אליו למליון מליונים של מעלות..., אבל בכל אופן המשפט שכתבת כי " אינסוף הוא כלי טוב להבנת תהליך פיזיקלי ולכיוון שלו, ולאנליזה מתימטית, אבל אין לו ממשות פיזיקלית." אם זה משפט במקומו, אז משפט זה יכול להוות לי כלי חשוב להבנתו ולהבנת העוסקים בו, אבל אני מתלבט קצת ביחס של משפט זה לגבי מהירות האור, כי היא כן סופית).

דניאל, תודה גם כן לך על המידע המעניין שהשארת בדרך אגב (שלא הייתי מגיע אליו כנראה למרות היותו קיים בויקיפדיה בערך שהצגת), רק הרשה לי לשאול בבקשה עשרה מליון מליוני מעלות, לפי מיטב הבנתי, זה סדר גודל של אלף מליארד מעלות, השאלות העולות מעצמן הן שתיים: א. איזה חומר בעולם יכול להחזיק מעמד מול חומר כזה? (לדוגמה, הסיבה שלא חופרים בור עד לאוסטרליה היא מפני שלא נמצא חומר שיכול להחזיק מעמד מול החום האדיר של גרעין הלבה, שהוא בסך הכל כ-6000 מעלות לפי מיטב זכרוני, אחרת הדרך הייתה קצרה בהרבה...). ב. השאלה השניה היא איך ניתן בכלל למדוד כזה חום, ולא רק מהסיבה הראשונה, אלא איזה כלי מכוייל כדי למדוד מספר מעלות כאלה? מוטיבציה - שיחה 15:25, 9 בנובמבר 2012 (IST)

החומר לא מחזיק מעמד. הוא הופך לגז כבר בסדר גודל הרבה יותר נמוך, ופיצוץ מימני הוא כבר מתפרק עוד יותר למיטב הבנתי. אני לא יודע אם בזה משתמשים, אבל ידוע לי שאפשר להשתמש במצלמה תרמית מסוגים מסוימים כדי למדוד טמפרטורות גבוהות. בלנק - שיחה 15:45, 9 בנובמבר 2012 (IST)

לא חשוב באיזה מצב צבירה הוא, שאלתי איך יש כלי בעולם שמסוגל להכיל חומר (במצב צבירה כלשהו - לרבות גז) כשמדת טמפרטורתו היא בת מליארדים מעלות חום. לכאורה אין דבר היכול לעמוד בפני חום כזה. מוטיבציה - שיחה 18:45, 10 בנובמבר 2012 (IST)

החומר לא מוכל בתוך כלי. . . בלנק - שיחה 19:20, 10 בנובמבר 2012 (IST)

אז כיצד הוא חוּמַם ונמדד? מוטיבציה - שיחה 20:50, 10 בנובמבר 2012 (IST)

זה נעשה בשיטת העבודה הסטנדרטית במאיץ חלקיקים. משקיעים אנרגיה עצומה בהאצת חלקיקים לאורך מנהרה ריקה (באמצעות מגנטים) למהירות קרובה למהירות האור, כשהחלקיקים מתנגשים זה בזה מתרחשות תופעות יחודיות שפולטות חלקיקים אחרים שנמדדים על ידי גלאים המקומים על דפנות המנהרה. באמצעות מדידת תוצרי ההתנגשות ניתן ללמוד את טבעה. דניאל • תרמו ערך 21:01, 10 בנובמבר 2012 (IST)

אפשר להמשיל את זה לדרך עבודתה של העין האנושית. העין מאפשרת לך ללמוד על דברים רחוקים מהישג ידך על ידי ניתוח ומדידה של חלקיקי האור (פוטונים) שנפלטים מהעצם אותו אתה בוחן. אינך צריך להכניס את ידך למדורה כדי להבחין שכמה מטרים לפניך בוערת אש. באופן דומה אפשר למדוד טמפרטורה של עצם מרוחק גם בלי לבוא עמו במגע. דניאל • תרמו ערך 21:07, 10 בנובמבר 2012 (IST)

דניאל, קודם כל תודה על ההמחשה בנושא מדידת החום וראיית העיניים, אהבתי אותה מאוד. אבל בכל אופן שאלתי כיצד חומר בעל חום רב שכזה (שוב, מליארדי מעלות חום!) הוכל על ידי מאיץ החלקיקים, הרי הוא היה אמור להינמס! ולהמשיך להמיס את האדמה שמסביבו. זהו חום אדיר שקשה להשיג אותו בשכל אפילו. המצב הזה (שסותר את הטבע), גורם לאדם קטן מן השורה, כמוני, לפקפק בהצהרה הזאת (שהטמפרטורה הגבוהה ביותר שהושגה על ידי אדם הגיעה לטמפרטורה מסדר גודל של עשרה מיליון מיליוני מעלות, בזמן שחומרים הקשים ביותר ביקום נמסים במליונית מעלות מהמעלות הנ"ל שהושגו במאיץ). מוטיבציה - שיחה 21:17, 10 בנובמבר 2012 (IST)

החלקיקים החמים לא נוגעים בדפנות המאיץ, התהליך מתרחש בריק, בנקודה קטנה מאד בתוך צינור גדול. יש קרינה וחלקיקים (תוצרים) שכן מגיעים אל הדפנות והגלאים, אך אין להם מספיק אנרגיה כדי להזיק להם. בניסויים שבהם מחזיקים פלזמה חמה מאד, משתמשים בכליאה מגנטית - שיטה שבה שדה מגנטי מחזיק את הפלזמה במקום, כי אין שום חומר שיכול לעמוד בטמפרטורות כאלה. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

הערה כללית לדיון, שאיננה באה לגרוע מדברי קודמי: אני לא מכיר את פרטי הניסוי הספציפי, אבל כשמדברים על טמפרטורה במאיצי חלקיקים בדרך כלל אין הכוונה באמת לטמפרטורה. הכוונה בהאצה של חלקיקים לאנרגיות שוות ערך לאלו של חלקיקים בטמפרטורה האמורה. וזה לא הבדל סמנטי, לא מתקיים שם שויי משקל תרמי. דבר שני, האנרגיה לכל חלקיק היא גבוהה, אבל האנרגיה הכללית של הקרן לא בהכרח כל כך גבוהה. בנסויים שבהם השתתפתי "יצרנו" טמפרטורה של 300 מליון קלווין, בהספק של חמישית וואט. בכל אופן, חלק ניכר מהמאמצים שמושקעים בפיסיקת חלקיקים מיועדים לדאוג לכך שהחלקיקים המואצים יפגעו כמה שפחות במקומות שאינם אמורים לפגוע בהם, על מנת למנוע נזקי קרינה או חימום יתר. משה פרידמן - שיחה 10:19, 11 בנובמבר 2012 (IST)

סיכום דיון: התשובה לשאלת השואל היא, שאין חסם עליון לגובה הטמפרטורה (למרות שיש חסם עליון למהירות). ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

איך בדיוק הגעת למסקנה המשונה הזו ? היא בודאי לא נובעת מהדיון הזה. בנצי - שיחה 03:04, 14 בנובמבר 2012 (IST)

היא נובעת ישירות מדבריו הנכונים של משתמש:ירון ק., כפי שניתנו בדיון הזה ביום 9 לנובמבר בשעה 07:44. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

חישוב

פיזיקאים, תראו רגע את החישוב שלי. מהירות חלקיק ממוצעת כפונקציה של טמפרטורה בגז אידאלי היא $v^{2}={\frac {3K_{b}T}{m}}$ כאשר m מסת מולקולה (מגעים לנוסחה מהשוואת אנרגיה קינטית לתרמית). אז $T={\frac {v^{2}m}{3K_{b}}}$ ובגבול של מהירות האור $T_{c}=\lim _{v\rightarrow c}{\frac {v^{2}m}{3K_{b}}}$. כלומר בהינתן מסת מולקולה ניתן לחשב טמפרטורה מקסימלית של החומר. היא מהירות תאורטית, "גבול בלתי מושג" אבל סופי. 109.65.212.246 16:14, 9 בנובמבר 2012 (IST)

בואנה, איזה פאדיחה. לקחתי אנרגיה קינטית קלאסית. חישוב שני:

${\frac {3}{2}}k_{b}T=\left({\frac {1}{\sqrt {1-v^{2}/c^{2}}}}-1\right)m_{o}c^{2}$

$T_{c}=\lim _{v\rightarrow c}{\frac {\left({\frac {1}{\sqrt {1-v^{2}/c^{2}}}}-1\right)m_{o}c^{2}}{{\frac {3}{2}}k_{b}}}=\infty$

ומכאן שאין גבול לאגניה מקסימלית. 109.65.212.246 16:21, 9 בנובמבר 2012 (IST)

עבור גז יחסותי מאד (מהירות שואפת ל c) צריך להיות 3kT ולא 1.5kT. הניסוח המדויק של חוק החלוקה השווה תלוי בקשר הפונקציונלי בין התנע והאנרגיה (נפיצה/דיספרסיה). ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אינטגרציה בחלקים

אני מנסה לבצע אינטגרציה לפונ' הבאה: x^3*e^(-x^2/2), באמצעות שימוש באינטגרציה בחלקים, אך ללא הצלחה מרובה. ניתן לראות את הפונ' בוולפרם פה. לא הבנתי איך מתבצע שם מעבר מסוים מ-x^3, ל-X^2. אביעד‏ • שיחה 15:07, 9 בנובמבר 2012 (IST)

קודם תעשה החלפת משתנים t=x^2 ואחרי זה אינטגרציה בחלקים. • בברכה, אמיר (שיחה), _{הקרב על באר שבע החל} 16:35, 9 בנובמבר 2012 (IST)

תודה רבה, את זה הצלחתי... יש למישהו רעיון לגבי אינטגרציה של (cosx)^4. (קוסינוס ברביעית של X)? אביעד‏ • שיחה 18:01, 9 בנובמבר 2012 (IST)

באופן כללי פולינום בקוסינוס וסינוס אפשר להפוך לצירוף לינארי של פונקציות מהצורה $\cos nx,\sin nx$. אפשר למצוא צירוף כזה באמצעות הגדרת הסינוס והקוסינוס דרך נוסחת אוילר (מופיע בערכים קוסינוס וסינוס). במקרה הזה וולפראם אלפא נותן את הזהות $\cos ^{4}x={\tfrac {1}{8}}(3+4\cos(2x)+\cos(4x))$. דניאל • תרמו ערך 18:08, 9 בנובמבר 2012 (IST)

לפני שנה התבקשתי למצוא אינטגרציה של sin^100 x ומצאתי באינטרנט אלגוריתם שמוריד חזקה ב2 וע"י שימוש בו אפשר לפתור גם ללא מחשב שפותר בצורה נומרית. ‏cheshin61‏ • שיחה • כ"א בכסלו ה'תשע"ג • 15:04, 5 בדצמבר 2012 (IST)

סימולציות פיזיקה במחשב

איך מגיעים למקצוע של לעשות סימולציות ממוחשבות עם גרפיקה של תופעות פיזיקליות? איזה קורסים צריך לקחת סטודנט לפיזיקה בשביל זה? 109.67.189.96 19:29, 9 בנובמבר 2012 (IST)

אני יודע שכל סטודנט להנדסת מכונות או הנדסת בניין עובר קורס של "גרפיקה למהנדס". אולי גם פיזיקאים? בלנק - שיחה 20:51, 9 בנובמבר 2012 (IST)

אין קורס( לפחות בטכניון) בשם "גרפיקה לפיזיקאים". יש "פיזיקה חישובית" (לא יודע אם זה קשור). 109.64.206.223 21:17, 9 בנובמבר 2012 (IST)

בסימולציות פיזיקליות הבעיה העיקרית זה החישובים עצמם, ולא הגרפיקה. כל תוכנה שמבצעת חישובים יכולה להציג גם בצורה גרפית את התוצאות. לדומה, במטלב יש יכולות גרפיות מאוד משוכללות, בנוסף ליכולות החישוביות המתקדמות. ‏Setreset • שיחה 21:29, 9 בנובמבר 2012 (IST)

אז איפה לומדים להשתמש בהם ברמה מקצועית? 109.64.206.223 21:59, 9 בנובמבר 2012 (IST)

יש קורסים ברמה הבסיסית, את עיקר המקצוענות רוכשים תוך כדי עבודה. שוב לדוגמה מטלב, יש בטכניון בפקולטה לחשמל וגם בפיזיקה קורסים שדורשים הגשת תוכניות כתובות במטלב, ובקורסים האלו מלמדים מטלב ברמה בסיסית. יש אין-ספור חוברות מודפסות ומדריכים באינטרנט בנושא. אם יש בעיה ספציפית שרוצים לפתור, האינטרנט עוזר מאוד, והרבה פעמים יש קטעי קוד (באינטרנט) שעושים חלק גדול מהעבודה. ‏Setreset • שיחה 23:43, 9 בנובמבר 2012 (IST)

מסכים עם סטריסט, אבל חייב למחות על הפרסומת המסיבית שמוסדות אקדמיים מספקים לתוכנה מסחרית (יקרה מאוד!!!) ולא בלעדית בשוק. גם אצלנו במסגרת קורסי החובה מלדמים ומשתמשים במטלב דווקא - ללא כל הצדקה. אני מנצל את הבמה כדי להציג בפני הקוראים כלי חלופי, לא הרבה פחות נוח והרבה יותר מתאים לפיסיקאים. מדובר בתוכנה ROOT המפותחת על ידי פיסיקאים עבור פיסיקאים, ומופצת בחינם לכל דורש. היא גם נכתבת בשפה סטנדרטית (c++), ועל כן מאפשרת תאימות עם כלים (חינמיים) אחרים העשויים לעניין פיסיקאים, כגון GEANT4. משה פרידמן - שיחה 21:52, 10 בנובמבר 2012 (IST)

א. השימוש ב-MatLab הוא אינטנסיבי מאוד גם במכון וייצמן, וכנראה במוסדות גדולים נוספים. אני משער שלחברות מסחריות יש כוח 'דחיפה' למוצרים שלהן, מעבר לשיקולי עדיפות של מוצר, משום שקבלת החלטת רכישה כרוכה בניסיון והיכרות עמוקה עם המוצרים המתחרים. לא תמיד מקבל ההחלטה הוא גם המשתמש במחלקה נתונה.

ב. האם ROOT תואמת את MatLab ודומותיה המסחריות ?

ג. כיצד ניתן להשיג את ROOT ואת GEANT4 ? אני מניח שחיפוש בגוגל יפתור את הבעיה, אלא אם כן, יש משהו שכדאי לדעת מעבר לכך. בנצי - שיחה 15:27, 11 בנובמבר 2012 (IST)

ROOT איננו חיקוי של מטלב. ROOT הוא כלי אנליזה שמפותח במעבדות Cern, המכיל את כל הכלים הדרושים לפיסיקאי ברמה הגבוהה ביותר. בדברים מסויימים הוא פחות נוח, ובדברים אחרים הוא יותר נוח. מבחינת יכולות לדעתי הוא חזק יותר. ROOT ו GEANT4 ניתנות להורדה בחינם באתר של Cern, ניתן לחיפוש פשוט בגוגל. (GEANT4 זו תוכנה שונה, המבצעת סימולציות מונטה קרלו של תהליכים פיסיקלים). כמובן, כמו כלי המשמש לעבודה נסיונית סטנדרטית, ROOT מתוארת במאמר שעבר ביקורת עמיתים, וצוטט למעלה מ 1500 פעם בספרות. משה פרידמן - שיחה 21:05, 11 בנובמבר 2012 (IST)

מסתבר שיש אפילו ערך בויקי אנגלית. משה פרידמן - שיחה 22:47, 11 בנובמבר 2012 (IST)

אני יכול גם להמליץ על ההרחבות החינמיות Numpy ו-Pylab לפייתון, באמצעותן ניתן לבצע בערך כל פעולה חישובית\גרפית שבד"כ מבצעים במטלב, עם היתרון הגדול של הפשטות וה"כיפיות" של פייתון. 94.159.238.173 18:48, 12 בנובמבר 2012 (IST)

סימון דיראק

יש לי מצב $\left|\psi \right\rangle =a\left|+\right\rangle +b\left|-\right\rangle$ ואופרטור A מטריצה 2 על 2 נתונה מספרית. אז ערך התצפית של A הוא $\left\langle \psi \right|A\left|\psi \right\rangle =\left({\begin{array}{cc}a&b\end{array}}\right)\left({\begin{array}{cc}\\\\\end{array}}\right)\left({\begin{array}{c}a\\b\end{array}}\right)$ או $\left\langle \psi \right|A\left|\psi \right\rangle =\left({\begin{array}{cc}a&b\end{array}}\right)\left({\begin{array}{cc}\\\\\end{array}}\right)\left({\begin{array}{c}a*\\b*\end{array}}\right)$

$\langle \psi |A|\psi \rangle =\left({\begin{matrix}a^{*}&b^{*}\end{matrix}}\right)\left({\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}}\right)\left({\begin{matrix}a\\b\end{matrix}}\right)$. בברכה, MathKnight (שיחה) 22:03, 9 בנובמבר 2012 (IST)

אחלה. האם יש איזה קשר מתמטי פשוט יחסית בין $ab^{*}$ לבין $a^{*}b$.? אני יודע שהמצב $\left|\psi \right\rangle =a\left|+\right\rangle +b\left|-\right\rangle$ מנורמל. 109.64.206.223 22:11, 9 בנובמבר 2012 (IST)

כן. $(a^{*}b)^{*}=b^{*}a$ ולכן $a^{*}b+b^{*}a=2\mathrm {Re} (a^{*}b)$. בברכה, MathKnight (שיחה) 22:26, 9 בנובמבר 2012 (IST)

תאוצה זוויתית

קיבלתי את שאלה זו: מצאו את התאוצה הזוויתית של גלגל ברדיוס R אם וקטור התאוצה הכוללת של נקודה על היקפו יוצר זווית של pi/6 עם כיוון התאוצה המשיקית באותה הנקודה בזמן t=1s לאחר תחילת התנועה.

מה שאני עשיתי - מכפלה סקלרית בין התאוצה הכוללת לבין התאוצה המשיקית שווה למכפלת הגודל שלהן כפול קוס' הזווית שביניהן. בסופו של דבר קיבלתי הבעה של θ דוטיים באמצעות θ דוט. וכך הבעתי את התאוצה המשיקית באמצעות θ דוט.

א. האם כדי לגלות את התאוצה הזוויתית, אני פשוט יכול לקחת את וקטור התאוצה המשיקית ולחלק אותו ב-R?

ב. מדוע ניתן לי הנתון של t=1s?

תודה, אביעד‏ • שיחה 15:34, 10 בנובמבר 2012 (IST)

היש עונה? אביעד‏ • שיחה 14:55, 12 בנובמבר 2012 (IST)

טור טיילור בפיזיקה

איך עושים טור טיילור בפיזיקה? במשך שנה וחצי חשבתי שאני יודע, אבל אני תקוע בתרגיל הזה כבר כמה שעות. מה הם עשו? איך פיתחו את הביטוי לטור טיילור? אני כבר קראתי את הערך האנגלי בפסקה המתאימה ועדיין לא מבין מה הם עשו. אני שואל רק לגבי סעיף 1.2. אולי זה לא טור טיילור אלא משהו אחר? כי אני לא רואה קשר. 79.181.236.201 16:38, 10 בנובמבר 2012 (IST)

למה זו הפסקה המתאימה? אין צורך בכמה משתנים. אם מניחים ש-$\ v^{2}-2gz$ קטן קטן מ-1, אז ניתן להשתמש בטור טיילור:

$\ {\frac {1}{\sqrt {1-x}}}=~1+{\frac {x}{2}}$

כאשר $\ x=v^{2}-2gz$. ירון • שיחה 19:16, 10 בנובמבר 2012 (IST)

זה אומר שהם שפוט לא ענו על השאלה ששאלו? הם ביקשו לפתח טור באיברים v^2 וgz אז הבנתי שהכוונה היא בטור ב2 משתנים. מוזר, אבל עונה על שאלה. 79.181.236.201 16:47, 11 בנובמבר 2012 (IST)

מה הייתה מטרתו של גלילאו בהמצאת הטרמוסקופ?

לפי מיטב ידיעתי, השיטה המדעית עובדת כך: (1) שואלים שאלה, (2) משערים מה תהיה התשובה, (3) מבצעים ניסוי, (4) תצפית (5) תוצאה (6) מסיקים מסקנות. מה הייתה שאלתו של גלילאו גלילי כאשר הוא ביצע את הניסוי בו הוא בנה תרמוסקופ? למישהו יש מידע בנושא - אולי מתוך כתביו שלו או מכתבי תלמידיו?. מוטיבציה - שיחה 19:02, 10 בנובמבר 2012 (IST)

גלילאו חי לפני שהועמדו יסודות הפילוסופיה של המדע כך שספק שהכיר בשיטיות השיטה המדעית. מעבר לזאת, גם מדענים בימנו לא בהכרח חושבים במונחים של השלבים הללו, גם אם זה תאור לא רע של מה שקורה בפועל. דניאל • תרמו ערך 19:47, 10 בנובמבר 2012 (IST)

בכל מקרה, מן הסתם אתה תסכים שהוא ביצע את הניסוי הזה או בנה את הכלי הזה מתוך מטרה (כגון לבחון משהו או להוכיח משהו) ולא באופן רנדומלי. וכעת השאלה היא מה הייתה מטרה זו שבגינה הוא ניגש לבנות את התרמוסקופ. מוטיבציה - שיחה 21:08, 10 בנובמבר 2012 (IST)

הפניה פיזיקה מודרנית

במקום לוח מודעות, נראה לי שהאנשים הרלוונטיים מסתובבים יותר בדף הזה: הפיכת פיזיקה מודרנית להפניה לערך התפתחות הפיזיקה במאה ה-20. דיון ונימוקים בשיחה:פיזיקה מודרנית. ‏Setreset • שיחה 23:01, 10 בנובמבר 2012 (IST)

סימטריה

שלום,

אני לוקח קורס בסיסי בסימטריה (לא למתמטיקאים). נאמר לי שלעצם מסוים יש ציר סיבוב שיקוף S8, ואני צריך לקבוע את פעולות הסימטריה ה"מתחייבות" מכך. אני לא מבין למה הכוונה בפעולות סימטריה המתחייבות מקיום אלמנט סימטריה כלשהו. אם אני לא יודע כלום על איך העצם נראה, איך אני אמור לדעת אילו פעולות מתחייבות מקיום אלמנט הסימטריה הנ"ל? תודה, 94.159.155.49 10:16, 11 בנובמבר 2012 (IST)

מרחב הילברט של ספין

בהרצאה בפיזיקה קוונטית נאמר שמרחב הילברט של תנועת החלקיק (המילטוניאן אורביטלי) ומרחב הילברט של הספין הם שונים. בגלל זה כשמדברים של מטריצת H של הספין (לדוגמה מטריצה 2 על 2 במרחב של ספין חצי) אז אסור לחבר לזה אנרגיה קינטית וכדו'. נשאלת השאלה, איפה נמצא המרחב של הספין חצי? האם זה אומר שספין הוא לא חלק בreal space? שזו "תנועה" במרחב שהוא מעבר למרחב התלת-מימדי שלנו? שאלקטרון הוא יצור שחי ב"עוד עולם" פרטי משלו וברגע שעושים מדידה הוא קורס ל"עולם שלנו"? כמו שאתם רואים אני מדבר טיפה לא פורמלי ומצפה לתשובה בהתאם (משהו שיעזור לי להבין אינטואיטיבית את הקונספט של ספין). 109.67.209.212 18:05, 11 בנובמבר 2012 (IST)

זאת משום שהוא נוהג כאילו היה לו תנע זוויתי של סיבוב עצמי, אבל להתנהגות זו אין מקבילה קלאסית. אילו באמת הסתחרר כך, מהירותו היתה צריכה לעלות על מהירות האור. מדובר בשתי תופעות שונות מהותית, ומה שאמרת על "עולם פרטי משלו" - אכן, עולם קוונטי לחלוטין, ללא אנלוג בעולם הקלאסי. בנצי - שיחה 18:49, 11 בנובמבר 2012 (IST)

אני לא אוהב את הנימוק שאילו היה מסתובב, מהירותו עולה על מהירות אור ולכן הוא לא מסתובב. אין שום סתירה לתורת היחסות במהירות עולה על מהירות האור. ראה "Faster-than-light" באנגלית (אני לא מדבר על טכיונים אלא על זה שלא נמסרת אינפורמציה). לגבי עולם פרטי משלו- אני לא סתם מדבר על זה שחוקי טבע קאלסיים לא תקפים לחלקיקים יסודיים. אני מדבר על רעיון שלכל אלקטרון יש "עולם פרטי משלו" ושהוא מועיל בטובו לבקר בעולם שלנו בזמן קריסה. אולי בעולם הפרטי הזה יש לו זכות לעשות "תנועה מוכללת" שהיא לא מרחבית (כלומר "תנועה" שהיא לא רוטציה או טרנסלציה). 109.67.209.212 19:01, 11 בנובמבר 2012 (IST)

א. "מואיל בטובו".

ב. אין "לא אוהב". אין מה לעשות - מדובר בתנע זוויתי בלתי אפשרי. אין מהירות העולה על מהירות האור, אלא אם כן מדובר בתווך חומרי שם חלקיקים יכולים להיות מהירים יותר מגלים א"מ, והדוגמא שלך לגבי מידע איננה רלוונטית. לא דיברתי על תקפות חוקים קלאסיים (ולכן גם הדיבור על 'קריסה' לא שייך) אלא על העדר אנלוג קלאסי, כלומר תופעה המופיעה רק ברמה הקוונטית, שזה משהו אחר.

ג. נכון, מדובר ב'תנועה' השקולה לקיומו של תנע זוויתי, ללא תנע זוויתי. גם המושג 'תנועה מוכללת' אינו רלוונטי.

ד. זו איננה הבעיה המוזרה היחידה שאינה מובנת עדיין בשום צורה, מלבד תצפיות ניסוייות. תופעה מוזרה אחרת היא 'תיאום המופעים' בין שני פוטונים שיצאו מאותו מקור, כשהאחד יודע את קורותיו של השני, כשה'מידע' על כך אמור לנוע מהר יותר מהאור (ראה ניסוייו של בל (בהעדר ערך עברי, ראה מאמר זה) ומשפט בל). תופעה נוספת היא אפקט אהרונוב-בוהם. בנצי - שיחה 19:23, 11 בנובמבר 2012 (IST)

מה שאתה אומר (אין דבר הנע מהר מ-C) סותר את מה שאני למדתי. נתנו לנו דוגמאות שבהם חישבנו מהירות של גל בפלאזמה וראינו שמהירות הפאזה גבוהה ממהירת האור, ומהירות החבורה קטנה ממהירות האור. את הסתירה כביכול ניתן ליישב אם מבינים שאין שום מעבר אינפורמציה על ידי הפאזה אלא יש רק על ידי החבורה. ראה בערך "Phase velocity":

The phase velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed thespeed of light in a vacuum, but this does not indicate any superluminal information or energy transfer.

זו הסיבה שהנימוק הזה לא נשמע לי משכנע. אין מעבר חומר, אנרגיה או אינפורמציה בסיבוב של כדור סימטרי סביב עצמו. צריך נימוק קצת יותר חזק מזה שיש סתירה ליחסות (כי אין).

אגב, למה לא קיבלת את המונח שהמצאתי של "תנועה מוכללת"? זה תופעה כמו תנועה מרחבית, אבל שבמהלכה הגוף לא נע ולא מסתובב כי הוא עושה תנועה לא במרחב הממשי אלא משהו אחר לא מובן לאנוש במרחבו הפרטי. 109.67.209.212 20:14, 11 בנובמבר 2012 (IST)

א. נכון מאוד: המגבלה היחסותית על מהירות האור אכן מתייחסת למהירות החבורה.

ב. מה זה "לא מובן לאנוש" ? זו תופעה אינהרנטית. בנצי - שיחה 20:23, 11 בנובמבר 2012 (IST)

תפרש בבקשה למה אתה מתכוון במילה אינהרנטי? 109.67.209.212 20:37, 11 בנובמבר 2012 (IST)

זו אינה כוונה פרטית, אלא מובנו של המונח: הכוונה היא לתכונה טבועה, מובנית, שהיא חלק בלתי נפרד ממהותה של הישות הנדונה. זאת בניגוד לגדלים פיזיקליים 'רגילים', להם יכולים להיות מקרים פרטיים כאלה ואחרים אותם ניתם לחשב מתוך איזשהו כלל יסודי. תכונת הספין איננה כזו - אין לה גדלים פיזיקליים אחרים בהם היא תלויה. בנצי - שיחה 20:46, 11 בנובמבר 2012 (IST)

נורא מעניין מה שאתה אומר. אתה אומר שתכונת הספין היא כמו מסה, מטען וכדו' כלומר תכונה "מובנת" בתוך אלקטרון ולא דבר התלוי בניסוי (כמו תנע, תנ"ז וגובה מעל לפני הים)- זו משמעות המונח אינהרנטי שהשתמשנו בו. אבל לספין יש תכונה שהוא משתנה בזמן! אנחנו רושמים מצב של אלקטרון ככה $|\psi >=a|+>+b|->$ והמקדמים לא חייבים להיות קובעים בזמן. כלומר יש תכונה קבועה שהיא גם מתפתחת בזמן? וחוץ מזה, מטען אי אפשר להפוך וספין כן ניתן להיפוך על ידי מכשיר. האם זה לא אומר שלאלקטרון יש מבנה פנימי ורכיבים כלשהם? 79.182.228.95 21:35, 11 בנובמבר 2012 (IST)

אגב, ל'תנועה מוכללת' יש משמעות אחרת קלאסית: ראה מכניקה אנליטית. בנצי - שיחה 21:41, 11 בנובמבר 2012 (IST)

מה שאתה הופך עם אופרטורים + - זה את כוון הספין ולא את גודלו, שנשאר קבוע. ‏Setreset • שיחה 23:10, 11 בנובמבר 2012 (IST)

אז אחרי שסיכמנו שספין הוא דבר פנימי ולא מרחבי, מה המשמעות של כיוון הספין? זה כיוון מרחבי, כלומר יש משמעות להגיד "ספין ימינה"? אם כן, איך מיישבים את הסתירה בין זה שמצד אחד ספין הוא לא סיבוב במובן גאומטרי-מרחבי ומצד שני יש לו כיוון (כלומר ציר סיבוב)? 79.179.211.137 23:38, 11 בנובמבר 2012 (IST)

ההשפעה השונה במרחב (בכיוון ולא בגודל) היא תוצאה של תכונה פנימית שלה שתי אפשרויות מנוגדות, בדומה למשל, למטען חשמלי, שהיא תכונה פנימית עם שתי אפשרויות כיווניות מנוגדות. האם אתה מסוגל להסביר שם את השוני בהשפעה המרחבית ? זה אותו סוג של בעיה, רק שלזו אנו 'רגילים' יותר. בנצי - שיחה 00:10, 12 בנובמבר 2012 (IST)

אבל זה לא אותו דבר. מטען הוא דבר קבוע ואין אפשרות להפוך אלקטרון לפוזיטרון. ספין אולי קבוע בגודלו, אבל יכול להשתנות בכיוונו. כלומר לספין יש משעות מרחבית- זה כיוון של משהו. המשהו הזה אולי לא סיבוב סביב עצמו, אבל עדיין יש תכונה מכוונת כלשהי. מסקנה: אלקטרון הוא בעל סימטריה גלילית ולא כדורית. 192.114.105.254 13:35, 12 בנובמבר 2012 (IST)

לא סימטריה גלילית, אבל בהחלט לא סימטריה ספרית. רוב החלקיקים לא סימטריים לשיקוף (כלומר לפעולת מראה). אני לא בטוח בהמשך ונא לקחת בערבון מוגבל מאוד, אבל אני חושב שחלקיקים עם ספין שלם יכולים להיות בעלי סימטריה ספרית (כאשר m_s=0), בדומה למספרים קוונטיים של תנע זוויתי, ראה גם אורביטל. ‏Setreset • שיחה 16:32, 12 בנובמבר 2012 (IST)

חידת מספרים

איך ניתן להגיע באמצעות שימוש יחיד בכל אחת מהספרות 3,4,5,6 ובפעולות חשבון בסיסיות (+,-,/,*) למספר 28? ניסיתי ולא הצלחתי. ים • שיחה • כ"ז בחשוון ה'תשע"ג • 18:13, 11 בנובמבר 2012 (IST)

פתח סוגריים (שש חלקי שלוש ועוד חמש)סגור סוגריים כפול 4 בלנק - שיחה 18:56, 11 בנובמבר 2012 (IST)

"יגעת ומצאת - תאמין". הקדמת אותי. בנצי - שיחה 19:09, 11 בנובמבר 2012 (IST)

החידה היא עבור כל רביעיות המספרים העוקבות שבקבוצה {10,...,1,2}. כלומר, הצג את המספר 28 באמצעות המספרים {1,2,3,4}, הצג את 28 באמצעות {2,3,4,5}, וכו'. 80.230.84.214 23:19, 11 בנובמבר 2012 (IST)

זיהוי גודל פיזיקלי

יש לי איזו בעיה שבה מופיע גודל שאני לא מבין את המשמעות שלו. נתונה אנרגיה $E=-0.5mAR^{2}cos^{2}(\theta )$ כאשר R זה רדיוס כדור הארץ וטטה זו זווית של קו הרוחב (טטה שווה אפס בקו המשווה ו-90 מעלות בקוטב). מה יכולה להיות המשמעות של A? יוצא לי שיש לו יחידות של 1 חלקי זמן בריבוע? 79.179.241.21 21:01, 11 בנובמבר 2012 (IST)

התשובה נכונה, בהנחה ש-m היא מסת הגוף (לא ציינת זאת). בנצי - שיחה 21:30, 11 בנובמבר 2012 (IST)

כן, m זו מסת גוף. איזו משמעות יש לאנרגיה שכזאת? A הוא תדירות בריבוע? האם הביטוי הזה הוא משהו מוכר? 109.67.217.193 21:37, 11 בנובמבר 2012 (IST)

שים לב ש-$\,R\cos(\theta )$ הוא מרחקו של הגוף מציר הסיבוב של כדור הארץ. עוזי ו. - שיחה 21:38, 11 בנובמבר 2012 (IST)

ולהשלמת התמונה, הביטוי שקיבלת הוא האנרגיה הקינטית שלך, כאשר אתה יושב מול המחשב, בעודך מסתובב ביחד עם כדור הארץ סביב צירו. A הוא המהירות הזויתית (של כדור הארץ סביב צירו) בריבוע. משה פרידמן - שיחה 22:26, 11 בנובמבר 2012 (IST)

ולעוד השלמה: מדובר במסלול שרדיוסו תלוי בקו הרוחב, ונתון בביטוי שנתן עוזי קודם. בנצי - שיחה 23:16, 11 בנובמבר 2012 (IST)

איפיון נקודה ע"י מספר

כידוע, עוצמת R בריבוע שווה לעוצמת R. אם כך, האם יש דרך מקובלת לאפיין כל נקודה במישור באמצעות מספר ממשי אחד בלבד? אם יש - מה השימושים שלה, ואיך מסמנים באמצעותה עקומות? (חתכי חרוט, לדוגמה) 212.76.116.207 22:41, 11 בנובמבר 2012 (IST)

יש התאמה חד-חד-ערכית ועל בין המספרים הממשיים לבין זוגות של מספרים ממשיים. אבל מכיוון שהתאמה כזו אינה *רציפה* (המרחבים אינם הומיאומורפיים), אין לה שום שימוש גאומטרי. בכל זאת, לשימוש מעניין בתופעה דומה עבור המספרים הטבעיים, ראה עקום פאנו. עוזי ו. - שיחה 00:10, 12 בנובמבר 2012 (IST)

אמנם כקבוצות, עוצמת הקבוצות זהה, אך בדרך כלל כשמדברים על R, חושבים עליו לא כעל קבוצה, אלא כעל מבנה עשיר יותר (מרחב טופולוגי, או אפילו יריעה דיפרנציאלית). אלא שאז, כמובן, R שונה מאוד מ $\,\mathbb {R} ^{2}$. לירן (שיחה,תרומות) 00:12, 12 בנובמבר 2012 (IST)

עוזי, אם תחזור על הבנייה של עקום פאנו כפי שהיא מופיעה בערך, רק שתחליף את פונקציית קנטור בפונקציה המופיעה כאן תקבל העתקה חח"ע ועל שהיא גם רציפה מקטע היחידה לריבוע היחידה. אפשר להרחיב את זה בקלות גם להתאמה חח"ע ועל שהיא רציפה מהישר (או מהקטע) למישור. זה כמובן לא הומאומורפיזם כי המקור של קבוצות פתוחות במישור יהיה מסובך ולא פתוח על הישר. לשואל, אם לא אכפת לך מהרציפות יש העתקה פשוטה בהרבה שתאפיין כל נקודה במישור באמצעות מספר: לנקודה $(0.a_{1}a_{2}a_{3}\ldots ,0.b_{1}b_{2}b_{3}\ldots )$ תתאים את המספר $0.a_{1}b_{1}a_{2}b_{2}a_{3}b_{3}\ldots$ (צריך לסדר דקויות של ייצוג עשרוני יחיד אבל זה רק במספר בן מנייה של נקודות וזה לא בעיה). זו התאמה של הריבוע לקטע, ואפשר להמשיך ככה ולחלק את המישור למספר בן מנייה של ריבועים ולהתאים אותם לחלוקה בת מנייה של הישר לקטעים. דניאל • תרמו ערך 19:29, 12 בנובמבר 2012 (IST)

שמש בגבעון דום

אם יום בהיר אחד יפסיק כדור הארץ להסתובב על צירו למשך יממה אחת, איזה שינויים יחוש האדם הסביר ברחוב? איך יושפע מזג האוויר מכך שזרם הסילון יישכך? לצורך העניין, נא להתעלם מהשאלה כיצד ישתהה לו סיבוב כדור הארץ ואיך ייבלם כמקשה אחת. בתודה, ליאור पॣ • כ"ז בחשוון ה'תשע"ג • 00:04, 12 בנובמבר 2012 (IST)

מלבד גל הצונאמי בגובה חמישה(?) קילומטר שישטוף ממערב?... עוזי ו. - שיחה 01:49, 12 בנובמבר 2012 (IST)

הצונאמי זה מה שמטריד אותך? והבריזה המערבית במהירות של כ-1,600 קמ"ש לא מפריעה? נראה לי שאפשר להניח שהאוויר והמים על תכולתם יעצרו באורח פלא יחד עם היבשה. לא שיש לי מושג מה יקרה אחר כך, אבל אפשר לשאול את רנדול מונרו, הוא בטח ידע. Easy n - שיחה 09:37, 12 בנובמבר 2012 (IST)

השאלה הזו בעייתית. אתה מבקש להתעלם מהשאלה איך הוא נעצר כמקשה אחת, ובעצם מתעלם מחוקי הטבע, ואז שואל מה חוקי הטבע מנבאים שיקרה. אתה לפחות צריך להגדיר אילו חוקים עדיין רלוונטיים בשאלה. אם הכל נעצר כמקשה אחת, בכל אופן, לא יהיה שום צונאמי ושום בריזה. התופעות הללו יקרו רק במידה והאדמה תיעצר אבל המים והאטמוספירה לא ייעצרו. אינני יודע מה המוטיבציה לשאלה, אבל אם אתה מעוניין לבחון את נושא הנס שבכותרת, מוטב לזכור כי בעולם שבו הנס הוא אפשרי, זה די מגוחך לשאול מהם חוקי הטבע. אם אפשר לעצור את סיבוב כדור הארץ, לדאוג לשאר התופעות זה כבר פינאטס. משה פרידמן - שיחה 10:51, 12 בנובמבר 2012 (IST)

אנסח מחדש את השאלה: אם היו לוקחים אדם מהרחוב ומעבירים אותו מכדור הארץ לכוכב לכת אחר, הזהה לכדור הארץ בכל מובן פרט לכך שאינו חג סביב צירו, איזה שינויים הוא יחוש בחוויות היום-יומיות שלו? אני בכוונה מנסה להימנע משאלת הדינמיקה של בלימת כוכב לכת שלם, עם כל המאגמה והיבשות והאוקיינוסים והאטמוספירה לשכבותיה. ממש כשם שסטודנט שנה א' הלומד על מטענים חשמליים הנעים במהירות יחסותית מתבקש להתעלם משאלות הנוגעות להאצת המטענים למהירויות הללו. ליאור पॣ • כ"ז בחשוון ה'תשע"ג • 11:39, 12 בנובמבר 2012 (IST)

חפש באינטרנט Tidal locking, לדוגמה [2] [3]. בויקיפדיה באנגלית אין מידע על ההשפעות של הנעילה על הכוכב, אלא רק על הפיזיקה שגורמת לתופעה. ‏Setreset • שיחה 13:09, 12 בנובמבר 2012 (IST)

מגניב! יש מאמר חופשי על כך (: תודה רבה! ליאור पॣ • כ"ז בחשוון ה'תשע"ג • 13:37, 12 בנובמבר 2012 (IST)

במקרה הזה "כדוה"א המזויף" עדיין מסתובב סביב צירו, אבל משלים סיבוב סביב עצמו באותו זמן שלוקח סיבוב סביב השמש. כלומר יממת הכוכבים מתארכת לשנה, ולא לאינסוף. יממת החמה מתארכת לאינסוף. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

תקנו אותי אם אני טועה: על פני 12 או 24 שעות, האדם הסביר לא אמור להבחין בין כדו"א המשלים סיבוב סביב עצמו אחת לשנה, לבין כדו"א שאינו מסתובב כלל. כך או כך השמש תאיר עליו פחות או יותר מאותו המקום ברקיע. ליאור पॣ • כ"ח בחשוון ה'תשע"ג • 11:43, 13 בנובמבר 2012 (IST)

כפי שענה האלמוני, השמש תאיר בדיוק מאותו המקום ברקיע. ההבדל הוא שהכוכבים יזוזו בקצת במהלך 24 שעות. ‏Setreset • שיחה 21:01, 14 בנובמבר 2012 (IST)

אם היינו בכוכב לכת דמוי כדור הארץ שנמצא בתהודת סיבוב-מסלול 1:1 עם השמש שלו (נעילה כבידתית), אזי בצד המואר היה מצב סטטי-השמש הייתה קופאת במקומה כך שלאחר שעתיים שלוש היינו שמים לב שמשהו מוזר- השמש פשוט תקועה במקום. גם בצד החשוך במקום לראות את הכוכבים נעים מערבה בקצב של כ-15 מעלות בשעה, היינו רואים את הכוכבים נעים מזרחה לאיטם, בקצב של כמעלה אחת ליום. אגב, ככל הנראה יש לא מעט כוכבי לכת חוץ-שמשיים עם נעילה כבידתית לכוכב האם שלהם. החבלן • שיחה • מועדון החלל הוויקיפדי 00:02, 15 בנובמבר 2012 (IST)

מתימטיקה – חידה קשה

פונקציה f מהקבוצה {4,...,3-,4-} אל הקבוצה {0,1,2,3} מקיימת את הדרישות הבאות: לכל n, מתקיים f(-n)+f(n)<=3. בנוסף, מתקיים f(-4)+f(-3)+f(-2) = f(2)+f(3)+f(4, ומתקיים f(-4)+f(-1)+f(2) = f(-2)+f(1)+f(4. אני צריך פונקציה כזאת, שעבורה הסכום s = f(-4)+f(-3)+…+f(4 הוא מרבי.

הרבה זמן ניסיתי לפתור. ראיתי שאי אפשר להשתמש בשיטת כופלי לגרנז', כי הטווח אינו מספרים ממשיים אלא שלמים. בנוסף, אי אפשר להשתמש באלגוריתם, שמגדיר פאון קמור לפי האי-שוויונים, ומחשב את ערך הפונקציה בקודקודים, כי ייתכן שהקואורדינטות של הקודקודים לא יהיו מספרים שלמים. אולי אפשר להגדיר את הפאון הקמור המרבי, שמוכל בפאון הנ"ל ושקודקודיו בנקודות בעלות קואורדינטות שלמות, אבל זה די מורכב. חוץ מזה, אמנם הסיבוכיות היא ליניארית במספר הקודקודים, אבל מספר הקודקודים הוא מעריכי, ולכן סיבוכיות כל החישוב היא מעריכית. (החידות הבאות הן עבור תחומים בגדלים 27, 81, 243, וכו', לכן אני לא יכול לאפשר סיבוכיות מעריכית.) אשמח אם יש למישהו אלגוריתם פולינומיאלי, או נוסחה פשוטה עבור הסכום s. 80.230.84.214 00:12, 12 בנובמבר 2012 (IST)

ניסוח יותר ידידותי של השאלה: נתון לוח בגודל 3x3. בכל תא כותבים מספר מתוך {0,1,2,3}. סכום המספרים בתאים נגדיים אינו עולה על 3. (עבור התא האמצעי יש הגבלה כלשהי, שאינה מענייננו כאן. ניתן להניח שהתא האמצעי הוא נגדי לעצמו.) סכום המספרים בשורה התחתונה שווה לסכום המספרים בשורה העליונה. סכום המספרים בעמודה השמאלית שווה לסכום המספרים בעמודה הימנית. 80.230.84.214 01:37, 12 בנובמבר 2012 (IST)

(איזו תועלת רצית להפיק מהצפנת השאלה בגרסה הפורמלית הקודמת?)

ומהן "החידות הבאות"? בלי זה לא ברור לאיזה פתרון אתה מצפה. עוזי ו. - שיחה 01:47, 12 בנובמבר 2012 (IST)

(חשבתי שמה שכתבתי מנוסח באופן לא ברור.)

לכל w, החידה בממד w היא כך: (כלומר, הלוח שכותבים בו את המספרים הוא בממד w. הממד של הבעיה הוא d, מבחינת כמות הנעלמים המופיעים באי-שוויונים.)

d=3^w.

for each n between -(d-1)/2 and (d-1)/2,
f(-n)+f(n) <= 3.
for each k between 1 and w,
sum {f(n) | The k-th digit of radix 3 representation of n is 1} = sum {f(n) | The k-th digit of radix 3 representation of n is 2}.

s = sum {f(n) | -(d-1)/2 <= n <= (d-1)/2}.

רוצים להגדיר את f, כך שיתקבל s מרבי. 80.230.84.214 12:51, 12 בנובמבר 2012 (IST)

שוב הצפנה. אתה רוצה למלא קוביה w-ממדית במשקולות, כך שמרכז הכובד יהיה במרכז ומספר המשקולות לאורך כל אלכסון לא יעלה על 3. אם תשים משקולת אחת בכל תא תקבל פתרון חוקי; הוכחת שבפתרון אופטימלי יש לפחות משקולת אחת בכל תא? עוזי ו. - שיחה 13:37, 12 בנובמבר 2012 (IST)

מספר המשקולות לאורך כל אלכסון לא יעלה על 3, אבל זה לא רק האלכסונים שמחברים בין הקודקודים. זה כולל גם "אלכסון" שמחבר את המרכזים של שתי צלעות נגדיות של הקוביה, "אלכסון" שמחבר את המרכזים של שתי פאות דו-ממדיות נגדיות של הקוביה, וכך הלאה.

אם מחשבים את מספר המשקולות לאורך האלכסון, כולל התא שבמרכז, כמובן שעדיף לקבוע שבמרכז לא יהיו משקולות, כי כל תוספת של משקולת למרכז מקטינה את כמות המשקולות בהרבה תאים אחרים.

אם אשים משקולת אחת בכל תא, אקבל פתרון חוקי, אבל לא אופטימלי. הנה דוגמא לפתרון חוקי, שבו חלק מהתאים ריקים, אבל מספר המשקולות הכולל הוא גדול ממספר התאים:

3 0 1

0 0 3

1 3 0

אני חושב, שדוגמא זו היא אחד הפתרונות האופטימליים עבור המקרה הדו-ממדי, כי במרכז חייב להיות 0, ויש 4 צמדים של תאים, שבכל אחד מהם יש לכל היותר 3, ולכן בסך הכל יש לכל היותר 12. איני יודע אם אפשר להגיע למצב, שבו כל 4 הצמדים הם מרביים. 80.230.84.214 18:07, 12 בנובמבר 2012 (IST)

בדקתי את כל האפשרויות עבור המקרה הדו-ממדי. ישנם 3 פתרונות אופטימליים, עד כדי סיבובים ושיקופים. בכולם מספר המשקולות הוא 11. 80.230.84.214 18:47, 12 בנובמבר 2012 (IST)

2 2 0 --- 3 0 1 --- 2 1 1

0 0 3 --- 0 0 3 --- 1 0 2

2 1 1 --- 1 3 0 --- 1 2 1

אבל זה לא נותן לי את התשובה עבור ממדים גדולים מ-2. 80.230.62.116 00:57, 13 בנובמבר 2012 (IST)

האם זה הגיוני

הועבר מויקיפדיה:הכה את המומחה

שסוללה של פלפון מתרוקנת דווקא כשהוא סגור ? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

סוללה איננה קופסת שימורים. היא מתפרקת על עצמה באיחסון ממושך, או באי שימוש ממושך במכשיר בו היא נמצאת. זו הסיבה מדוע במדריכי הפעלה של מצלמות, למשל, מבקשים להוציא את הסוללה/ות במקרה של חוסר שימוש ממושך. בנצי - שיחה 11:53, 13 בנובמבר 2012 (IST)

התפשטות בפיזיקה

מה מתאר המונח "התפשטות" בפיזיקה? (האם הכוונה להתפשטות במובן של ההפך מהיצרות?) "גלילאו בנה מתקן למדידת הפרשי טמפר' שהיה מבוסס על התפשטות האוויר עם עליית הטמפרטורה" מהי מהות התפשטות האוויר במהלך ניסויו של גלילאו? מוטיבציה - שיחה 17:41, 13 בנובמבר 2012 (IST)

כשגז (כמו אוויר) מתפשט הכוונה היא שהוא מתפזר על נפח רחב יותר, כלומר יש ירידה בצפיפות שלו. כשגזים מתחממים הם מתפשטים על שטח רחב יותר, ובגלל גם המשקל הסגולי שלהם יורד, והם שוקלים פחות - מפעילים פחות לחץ. זאת הסיבה שאוויר חם עולה למעלה, וככה גם פועל כדור פורח שעובד על אוויר חם. בלנק - שיחה 18:18, 13 בנובמבר 2012 (IST)

כמה תיקונים:

א. גז אינו מתפשט (בדר"כ) עפ"נ שטח, אלא מתפשט בנפח.

ב. התחלת לדבר על שינוי בצפיפות הגז, שהוא שינוי במסה הסגולית שלו. אין צורך לעבור לדבר על משקל סגולי. אין הם היינו הך.

ג. מתשובתך לא ברור מדוע ירידה בצפיפות >> פחות לחץ, וגם לא ברור למה אויר חם עולה. ההסבר לעניין הראשון הוא העובדה שבצפיפות נמוכה יותר מס' החלקיקים הפוגעים ליחידת זמן קטן יותר. לחץ הוא המדד המקרוסקופי לתנע הנמסר בהתנגשויות אלה. אויר חם עולה כתוצאה מכך שהלחץ האוירוסטטי החיצוני מעליו, נמוך יותר מזה השורר מתחתיו, עפ"י עקרון ארכימדס.

ד. כדור פורח יכול לעבוד גם על גזים שצפיפותם נמוכה מזו של האויר. בנצי - שיחה 19:03, 13 בנובמבר 2012 (IST)

אז כשהחומר עולה בתרמוסקופ זה ביטוי לצפיפות החומר בחלק האורירי או שזה ביטוי להתפשטות החומר בחלק האורירי? מוטיבציה - שיחה 19:15, 13 בנובמבר 2012 (IST)

כשהצפיפות יורדת, המרחקים הממוצעים בין החלקיקים גדלים, וממילא החומר מתפשט - תוצאה הכרחית. בנצי - שיחה 19:21, 13 בנובמבר 2012 (IST)

כדי לראות אם הבנתי את הדברים לאשורם, אכתוב כאן את הדברים לסיכום ואם טעיתי אשמח לקבל תיקון: כשהחומר עולה במד התרמוסקופ, אז זה מעיד על כך שהאוויר התכווץ שם (במד למעלה). כשהחומר יורד במד התרמוסקופ, אז מעיד על כך שהאויר התרחב שם ולכן הוא 'דוחף' או לא מאפשר לחומר לעלות. האם זה נכון? מוטיבציה - שיחה 19:38, 13 בנובמבר 2012 (IST)

האם מספר שואף לעצמו?

לעניין חשיבות מרובה. האם מספר שואף לעצמו? דוגמא: האם 5 שואף לעצמו? האם הוא לא יכול לשאוף לעצמו כי הוא כבר הגיע לעצמו? האם הוא הגיע לעצמו ועדיין שואף לעצמו? אשמח לתשובה מפורטת עם דרך ההוכחה. תודה מראש, סטודנט לתואר ראשון במתמטיקה.

כסטודנט למתמטיקה אתה בוודאי יודע שהתשובה תלויה בהגדרת המושג "שואף". הפונקציה הקבועה f(x)=5 שואפת בכל נקודה a לערך 5 (זה הגבול שלה ב-a). הסדרה הקבועה a_n=5 שואפת לגבול 5. אם תמציא משמעות הולמת למושג השאיפה עבור מספרים, יתכן שגם הקבוע 5 ישאף לעצמו, אם כי לא ברור מה יצא לו מזה. עוזי ו. - שיחה 20:05, 13 בנובמבר 2012 (IST)

משקל של חפץ קשור בחוט בנוזל

אם אני לוקח כוס עם מים (או כל נוזל אחר) ומניח אותה על משקל. לאחר מכן, אני קושר משקולת קטנה בחוט, ומשקיע אותה בתוך הכוס (בהנחה ולא נשפך נוזל כתוצאה מכך). האם ייראה שינוי במשקל? איך, כמה, ולמה? תודה, אביעד‏ • שיחה 20:01, 13 בנובמבר 2012 (IST)

א. אתה משתמש באותו מונח - משקל, פעמיים, בשני מובנים שונים. הראשון צ"ל מאזניים ולא משקל, שהוא סלנג שלא יכירנו מקומו ביחוד כאן.

ב. משקל הוא כוח. הוא התגובה לכוח הנורמלי או לכוח המתיחות, כמו במקרה שאתה מתאר. כשהמשקולת בשיווי-משקל בתוך הכוס, היא נמצאת תחת פעולתם של 3 כוחות: כבידה כלפי מטה (mg), מתיחות - כלפי מעלה, וכוח ציפה כלפי מעלה, הנובע מחוק ארכימדס (על הגוף השקוע פועל כוח התנגדות כלפי מעלה, השווה למשקל הנוזל שנדחה מפני הגוף). כלומר, כוח הכבידה מאוזן ע"י שני כוחות: המתיחות וכוח הציפה, ומכאן שהמתיחות קטנה יותר מאשר במצב בו המשקולת תלויה באויר, ולכן גם משקלה הנמדד קטן יותר. כתוב לעצמך את הביטוי בצורה מפורשת, והמסקנה תתקבל בקלות. בנצי - שיחה 20:48, 13 בנובמבר 2012 (IST)

הוא שואל אם משקל הכוס עם המים ישתנה, כתוצאה מהכנסת המשקולת הקשורה לתוך הכוס. לא אם משקל המשקולת ישתנה. 80.230.62.116 21:29, 13 בנובמבר 2012 (IST)

זה לא ברור מהאופן שהשאלה מנוסחת. בכל מקרה, ממערכת שיקולים מאוד דומה - גם משקל הכוס ישתנה, שכן פועל עתה על הכוס כוח חדש היוצר שיווי-משקל חדש. בנצי - שיחה 21:45, 13 בנובמבר 2012 (IST)

מהו הכוח שפועל על הכוס? 80.230.62.116 22:04, 13 בנובמבר 2012 (IST)

שים לב להגדרת המשקל בתחילת תשובתי הקודמת. משקל המשקולת פועל על מי הכוס, והוא התגובה לכוח הציפה שהמים מפעילים עליה, כלומר, על המשקולת. בנצי - שיחה 22:10, 13 בנובמבר 2012 (IST)

לאחר הכנסת המשקולת לכוס, האם מדידת המאזניים תציג את המסה של כוס המים ללא המשקולת? האם היא תציג את סכום המסות של כוס המים והמשקולת? האם היא תציג את סכום המסות, פחות המסה של מים בכמות שנפחה שווה לנפח המשקולת? 80.230.90.250 00:12, 14 בנובמבר 2012 (IST)

א. אתה מבלבל בין משקל לבין מסה. נא עקוב אחרי השלבים שתיארתי קודם. אין תחליף לזה.

ב. שים לב להסבר המופיע בתגובתי להלן, המתייחסת בפירוט למציאת משקל הכלי במצב החדש. בנצי - שיחה 02:06, 14 בנובמבר 2012 (IST)

המאזניים יראו תוצאה גבוהה יותר. ההפרש בין המשקלים יהיה שווה במקרה זה למשקל של המים אותו נפח המשקולת יידחה. זאת אומרת התוצאה על גבי המאזניים תהיה (המים + הכוס + משקל המים הנדחים על ידי נפח המשקולת). 217.132.211.12 01:22, 14 בנובמבר 2012 (IST)

א. נכון, אבל אינך מסביר מדוע זה כך. מלבד זאת, התיאור אחרי המשפט הראשון לא ברור ומבלבל: מנקודת המבט של הכלי אין צורך בדחיה, מאחר וכוח זה פועל על המשקולת ולכן יופיע בתרשים הכוחות הפועלים עליה. וחוץ מזה: ידחה ולא יידחה.

ב. הסיבה לכך היא בדיוק ההסבר אותו נתתי בתגובה מוקדמת יותר, רק שהפעם הוא מיושם לכלי: שרטט משטח המייצג את כף המאזניים, ועליו צייר כלי עם מים בהם שקועה משקולת התלויה בחוט. שרטט כעת את הכוחות הפועלים על הכלי: הכבידה שעל הכלי, כלפי מטה; משקל המשקולת, כלפי מטה; הכוח הנורמלי שכף המאזניים מפעילה על הכלי, כלפי מעלה. כאמור, במצב שיווי-משקל הכוח הנורמלי (כלפי מעלה) מאזן את סך הכוחות כלפי מטה, כלומר הוא משתווה לסכומם. כעת, מאחר והמשקל המדוד של הכלי הוא התגובה לכוח הנורמלי, הרי שהוא יהיה גדול יותר בהשוואה למשקלו הרגיל (השווה בערכו לכבידה הפועלת על הכלי - mg). בנצי - שיחה 02:06, 14 בנובמבר 2012 (IST)

דוגמה נוספת לשאלת השואל, האם כאשר מונח על המשקל כוס שמכיל מים עד חציו, ואדם תוקע קצה אצבעו לתוכו, האם משקל הכוס ישתנה בעקבות כך. להבנתי המשקל לא ישתנה במאומה, שכן האצבע לא מכבידה על המשקל, מכיוון שהוא מחובר ליד שנושא אותו. טיפוסי - שו"ת 02:19, 14 בנובמבר 2012 (IST)

הכיוון שלי היה כזה: אם המשקולת הייתה נחה ללא לחוט בכוס, מובן שכל משקלה נוסף היה למשקל הכולל. אך מכיוון שהיא תלויה בחוט, חלק מהכוח פועל כלפי מעלה (כלומר החוט, לוקח חלק מהכוח שמופעל על המים). הנחתי שהכוח שמפעילה המשקולת כלפי מטה, כלומר על המאזניים, הוא אותו הכוח שהמים מפעילים עליו - כלומר כוח הציפה - מכפלת הצפיפות בנפח וב-g. אבל זה לא יצא נכון... אביעד‏ • שיחה 07:31, 14 בנובמבר 2012 (IST)

זה צריך להיות נכון לפי חוק ארכימדס, וזה אכן יוצא נכון בניסויים שאני ביצעתי. בדוק שנית את הניסוי - אולי, למשל, המשקולת צפה במים ואינה שקועה לחלוטין? אם כן אז הנפח הרלוונטי הוא רק הנפח שמתחת לפני המים. אולי המשקולת סופחת מים? אם כן אז הנפח אינו הנפח החיצוני. אולי החוט הוא בעל נפח משמעותי? אולי בטעות המשקולת נוגעת בדפנות או בתחתית? אולי המשקל (המכשיר) לא טוב? ‏Setreset • שיחה 20:56, 14 בנובמבר 2012 (IST)

פרס נובל למדע

הועבר מויקיפדיה:הכה את המומחה

האם היו אנשים שקיבלנו פרס נובל למדעים והאנשים האלא לא היו בעלי תואר אקדמאי מתקדם? 79.179.211.137 21:41, 13 בנובמבר 2012 (IST)

לא. בנצי - שיחה 22:14, 13 בנובמבר 2012 (IST)

בהנחה שתואר אקדמאי מתקדם, הוא תואר שני או שלישי ומעלה. התשובה שנתת שגויה. ל Koichi_Tanaka יש תואר ראשון בלבד. ואני בטוח שיש עוד כמה שהם בעלי תואר שני בלבד. בכל מקרה, הסוגיה המעניינת היא מה היה מעמדם האקדמאי בעת שעשו את המעשה שהוביל לזכייתם בפרס הנובל. כמדומני לאלברט איינשטין היה תואר ראשון בלבד בשנת 1905. בברכה, --איש המרק - שיחה 00:57, 14 בנובמבר 2012 (IST)

אכן, והערך מציין שהוא היחידי עם הישג כזה, בתחומי המדעים. יוצא מהכלל המעיד על הכלל - שאין כאלה, כלומר בתחומים אלה זה לא עובד אחרת, ולא יכול לעבוד אחרת, ומבחינה זו התשובה שנתתי אינה בדיוק שגויה. אגב, כדאי גם לבדוק לגבי בראג הבן, שקיבל את הפרס יחד עם אביו בהיותו עדיין צעיר מאוד. שווה בדיקה. בנצי - שיחה 03:21, 14 בנובמבר 2012 (IST)

אחרי בדיקה: היה לו אז כבר תואר מתקדם (איזה ?), אבל 'הישגו' הבולט הוא גילו: הוא חתן הפרס הצעיר ביותר (לפחות בפיזיקה, ויתכן שבכלל), בהיותו בן 25 בלבד. האיש שלך היה בן 43. בנצי - שיחה 03:37, 14 בנובמבר 2012 (IST)

הערך מציין שהוא היחידי שזכה בפרס נובל ונותר עם תואר ראשון, אבל כמו שציינתי זה פחות מעניין, מה שיותר מעניין זה, כמה אנשים זכו בפרס בזכות גילויים, פיתוחים או המצאות שנעשו לפני שהיה להם תואר מתקדם. זה די ברור שאנשים שפירסמו מאמר פורץ דרך בתחום אקדמי יקבלו אם ירצו בכך תואר שני או שלישי. בברכה, --איש המרק - שיחה 18:06, 14 בנובמבר 2012 (IST)

רודולף מוסבאואר קיבל את הפרס על תגלית שגילה בעת הדוקטורט שלו. eman • שיחה • ♥ 23:37, 14 בנובמבר 2012 (IST)

מעלות חום

הועבר מויקיפדיה:הכה את המומחה

מה הטמפרטורה הממוצעת שסיר ממתכת מגיע אליה בשימוש בו בעת בישול והרתחה? טיפוסי - שו"ת 01:26, 14 בנובמבר 2012 (IST)

כל עוד המים (בדר"כ אלו מים בבישול) לא התאדו לגמרי, גוף הסיר לא יעבור 100⁰C (טמפ' הרתיחה של המים), מאחר והטמפ' אינה עולה עד שהמעבר מהמופע הנוזלי למופע הגזי (אדים) לא יושלם. בנצי - שיחה 01:40, 14 בנובמבר 2012 (IST)

הכוונה שהסיר משתווה לחום המזון שבתוכו? וכך חומו של מחבת עם שמן על האש יגיע לחום כמעט כפול מסיר עם מים? טיפוסי - שו"ת 01:55, 14 בנובמבר 2012 (IST)

א. נכון, טמפ' הכלי לא יכולה לעבור את טמפ' הרתיחה מהסיבה שתיארתי קודם, כל עוד כמובן, היא מכילה נוזלים.

ב. לא לחום כמעט כפול, אלא לטמפ' כמעט כפולה - מושגים אלה אינם היינו הך. אגב, תחום טמפ' הרתיחה של שמני בישול הוא בקירוב, 150-170 מעלות צלזיוס - תלוי בסוג השמן; שמן זית למשל, רותח מוקדם יחסית, ולכן אינו מתאים לטיגון. בנצי - שיחה 02:17, 14 בנובמבר 2012 (IST)

אתה בטוח? זה חדש לי. אני יודע שהמים לא יעברו את טמפ' הרתיחה, אבל לגבי הכלי זה חדש לי. אני גם מתקשה להבין למה זה נכון. משה פרידמן - שיחה 09:01, 14 בנובמבר 2012 (IST)

בגדול דבריו של בנצי כמעט נכונים. הטמפ' היא רציפה ברמה המאקרו, אמנם יש התנגדות מגע בהולכת חום בין חומרים שונים, כמו כן יש מעט מאוד הבדל בטמפ' בין הדופן הפנימית לחיצונית של הסיר כיוון שהסיר מוליך חום מצויין. לדעתי ההתנגדות חום בין המים לסיר זניחה ממש וכך גם ההבדלים בין דפנות הסיר כך שלמעשה הוא לא יהיה בעל טמפ' גבוהה יותר מהמים. ♠ גיל כ. (שיחה) ♠ מיפוי ויקיפדיה ♠ 13:14, 14 בנובמבר 2012 (IST)

למה הטמפרטורה רציפה ברמת המקרו? (ומה זה בכלל?) ולמה אתה חושב שהסיר מוליך חום מצויין? ואם הסיר מוליך חום מצויין, האם זה אומר שיש מעט הבדל או הרבה הבדל בין הדופן הפנימית והחיצונית? אני אנסה לחשוב על זה בצורה מסודרת, אבל כל אחד מהנ"ל לא טריוויאלי בעיני. משה פרידמן - שיחה 13:49, 14 בנובמבר 2012 (IST)

לדעתי, לאחר בדיקה חפוזה, זה לא נכון. אי אפשר לטעון ביחד שמוליכות החום מצויינת, שאין אי רציפות בטמפרטורה, ושהטמפרטורה החיצונית והפנימית של הסיר קרובות זו לזו - אלא אם כן טמפרטורת הבעירה של הגז קרובה לטמפרטורת הרתיחה של המים. בכל אופן, מוליכות החום של הנירוסטה נמוכה, סירים רבים הינם עבים בתחתיתם, מה שמגדיל את הפרשי הטמפרטורה בין השפה החיצונית והפנימית (ומשפר את אחידות הבישול), ובהחלט תתכן אי רציפות משמעותית בין שפת הסיר הפנימי לתבשיל עצמו. איפה אני טועה? משה פרידמן - שיחה 14:13, 14 בנובמבר 2012 (IST)

אני מסכים איתך. בדיוק בגלל שטמפרטורה וחום אינם אותו דבר, זה לגמרי מסתדר שהסיר מגיע ל-400 מעלות, בעוד שהמים הצמודים אליו אינם מגיעים אפילו לרתיחה - משום שמוליכות החום שלהם היא גבוהה מספיק לפזר את החום המוזרם מהגז דרך הסיר, אל שאר המים בכלי. אם מתעלמים מכך שבסופו של דבר המים רותחים, אפשר להסתכל על הדקות הארוכות שעד הרתיחה כמצב קוואזי-עמיד, שבו יש שכבה תחתונה בטמפרטורה של 500 מעלות - הגז - שמעליה שכבת מתכת שלפי הטענה היא בפחות מ-100 מעלות, ומעליה נפח נוזלים שגם הוא בפחות מ-100 מעלות. זה אינו מצב עמיד הגיוני, בגלל שמוליכות החום של המתכת הרבה יותר טובה משל המים. לכן לפי משוואת החום המתכת צריכה להיות בטמפרטורה קרובה לזו של הלהבה. 87.68.83.14 17:58, 17 בנובמבר 2012 (IST)

מצד שני, לפי אותו טיעון, הדופן הפנימית של הסיר, שנוגעת במים, מעבירה להם חום ולא יכולה להיות חמה מהם במצב יציב. ייתכן שהשאלה לא מוגדרת בצורה מדויקת, ושהתשובה המלאה היא שהדופן החיצונית של הסיר היא חמה מאוד, כמעט בטמפרטורת הגז, והדופן הפנימית היא בטמפרטורת המים, כלומר מגיעה ל-100 מעלות לכל היותר כל עוד יש מים בכלי. אבל זה אומר שיש הפרש טמפרטורות גדול מאוד בין דפנות הסיר, שזה קצת מפתיע. 84.229.18.52 19:41, 17 בנובמבר 2012 (IST)

אינני בטוח לגבי טמפ' הגז שאתה מציין - האם מולקולות הגז פולטות קרינה א"מ בתחום הנראה כבר בטמפ' זו ? בנצי - שיחה 15:35, 18 בנובמבר 2012 (IST)

בהמשך להערה הקודמת: טמפ' הגז שאתה מציין - 500⁰C, אינה נכונה. טמפ' הלהבה אינה אחידה, וכל חלק בה מקרין בתחום טמפ' אחר, המתבטא באורכי הגל בהם הוא קורן, ובכל מקרה, הטמפ' גבוהה יותר. ככל שאורכי-הגל קצרים יותר, כך הטמפ' המתאימה גבוהה יותר. הטמפ' של החלק הכחול בלהבה, למשל, הינה כ-1,500⁰C. עיין ערך להבה. בנצי - שיחה 21:21, 19 בנובמבר 2012 (IST)

אכן, כך - הסיר לעולם לא יהיה בטמפ' אחידה, בשל המימשק עם מקור האנרגיה (אין שיווי-משקל תרמי). כלומר, מתקיים לרוחב תחתיתו (בעיקר, בין שני המשטחים) גראדינט טמפ' תלול למדי, ששיפועו משתנה כל העת. כוונת דבריי המקוריים (למעלה) היתה שהנקודה התחתונה של גראדינט זה אינה עוברת 100⁰C, כל עוד מצויים מים בסיר, ובמילים אחרות, המים לא 'נותנים' למשטח הפנימי לעלות מעבר לטמפ' זו. בנצי - שיחה 15:35, 18 בנובמבר 2012 (IST)

זה לגמרי לא היה ברור מתשובתך הנחרצת לעיל. בנוסף לא סביר שטמפ' תחתית הסיר גם מהצד הפנימי שלו תוגבל לרמת טמפ' המים שעליהם. טיפוסי - שו"ת 15:49, 18 בנובמבר 2012 (IST)

היא עדיין נחרצת, בודאי במונחים של טמפ' ממוצעת עפ"י שאלתך. למה לא סביר ? אין בטבע מעבר חד. אני מקווה שהמונח גראדינט ברור לך, שכן המעבר בין המשטח הפנימי של הסיר לבין השכבה התחתונה של המים אינו חד. בנצי - שיחה 23:34, 18 בנובמבר 2012 (IST)

בדיקת טעות בהסתברות

ההסתברות לזכות ב-100 ש"ח במשחק מזל היא 0.2; ההסתברות לזכות ב-200 ש"ח היא 0.1; וההסתברות לא לזכות כלל היא 0.7. אדם משחק שני משחקים, מה ההסתברות שיזכה בדיוק ב-200 ש"ח? (התשובה שלי היא 0.11 אבל התשובה בספר היא 0.18. מי צודק?) 176.13.83.194 03:49, 14 בנובמבר 2012 (IST)

מחבר הספר צודק. יש כאן 3 מאורעות זרים, שבכל אחד מהם האדם זוכה בדיוק ב-200 ש"ח. מאורע א: 100 ש"ח במשחק הראשון, 100 ש"ח במשחק השני. מאורע ב: 200 ש"ח במשחק הראשון, 0 במשחק השני. מאורע ג: 0 במשחק הראשון, 200 ש"ח במשחק השני. המשחק הראשון אינו תלוי במשחק השני. לכן ההסתברות למאורע של רווח x במשחק הראשון ורווח y במשחק השני, שווה למכפלת ההסתברות של המאורע של רווח x במשחק הראשון וההסתברות של המאורע של רווח y במשחק השני. ההסתברות לכך שמאורע א יקרה היא 0.2*0.2=0.04. ההסתברות לכך שמאורע ב יקרה 0.1*0.7=0.07. ההסתברות לכך שמאורע ג יקרה היא 0.7*0.1=0.07. שלושת המאורעות הם זרים, לכן ההסתברות למאורע של זכייה ב-200 ש"ח, שווה לסכום ההסתברויות של שלושת המאורעות, כלומר, 0.04+0.07+0.07=0.18. 80.230.90.250 04:08, 14 בנובמבר 2012 (IST)

גרדיאנט בפיזיקה

מה מתכוון פיזיקאי כשהוא אומר "קיים גרדיאנט"? דוגמה לשימוש כזה: "מחזיקים את המערכת בגדריאנט טמפרטורות". 109.67.221.231 21:50, 14 בנובמבר 2012 (IST)

יודע מהו קצב ? בשפה מתימטית, זהו שיעור השינוי בגודל נתון ליחידת זמן, כאשר שיעור זה קבוע, ובאופן כללי, זוהי נגזרתו של גודל זה לפי הזמן, שכן זו נותנת את הערך הרגעי של הקצב. גראדינט נותן משהו דומה, אבל לא ליחידת זמן, אלא ליחידת העתק, כלומר ליחידת רוחק מראשית הצירים, או נגזרתו של גודל נתון לפי הרוחק מהראשית (בציר x או בציר y או בציר z, או בכיוון ההעתק השקול של שלושתם, תלוי מה מחפשים). בהתייחס למשפט שלך, מדובר במורד טמפ' עפ"נ המערכת, כאשר בקצה אחד שלה הטמפ' הגבוהה ביותר, ובקצה השני שלה - הנמוכה ביותר. בסיכום: זהו שיעור השינוי בטמפ' ליחידת אורך או נגזרת הטמפ' לפי המקום עפ"נ המערכת הנתונה, תלוי במקרה. בנצי - שיחה 22:41, 14 בנובמבר 2012 (IST)

בתמצות, הכוונה היא שהטמפרטורה היא פונקציה של המיקום. ובפרט שיש הפרשי טמפרטורות בין אזורים שונים במערכת (ואז חום יזרום מהאזורים בטמפרטורה הגבוה היותר לאזורים בטמפרטורה הנמוכה יותר). eman • שיחה • ♥ 23:00, 14 בנובמבר 2012 (IST)

עזרה בביצוע אינטגרל

שלום חברים, אשמח אם תעזרו לי לבצע אינטגרציה ל-2x/(2x^2+1)dx. לא כל כך הבנתי את ההצבע של וולפרם. תודה, אביעד‏ • שיחה 12:14, 16 בנובמבר 2012 (IST)

$\log(f)'={\frac {f'}{f}}$. עוזי ו. - שיחה 12:30, 16 בנובמבר 2012 (IST)

תודה. שאלה נוספת, התבקשתי לעשות אינטגרציה ל-cosh בתחום 0 עד 1. התרגיל נכלל בקטגוריה של אינטרלים לא אמיתיים. אך איני מבין מדוע. גם cosh מוגדר לכל x. אין בעיה לא ב-0 ולא ב-1, כנל גם לגבי האינטגל שלו sinh. אז מדוע איני יכול פשוט להציב רגיל? אביעד‏ • שיחה 14:57, 16 בנובמבר 2012 (IST)

מספר ללא הצגה עשרונית

האם קיים מספר (אם קיים אחד אז יש אינסוף) שאין לו הצגה שעשרונית מקורבת (נגיד 3-4 ספרות אחרי הנקודה)? אם יש מספר כזה, האם ניתן להציג אותו כפונקציה (כמו לרשום שורש מאקספוננט של פונקציה טריגונומטרית של מספר ממשי או כפתרון של איזו משוואה מסובכת וכד')? 79.183.203.55 13:48, 16 בנובמבר 2012 (IST)

על מספר ממשי אפשר לחשוב כנקודה על הישר הממשי. בהינתן נקודה כזו אתה יכול להסתכל בין איזה שני מספרים טבעיים היא נמצאת. זה ייתן את הספרות לפני הנקודה. אחר כך תחלק את הקטע בין שני הטבעיים ל-10 חלקים שווים. זה ייתן לך את הספרה הראשונה אחרי הנקודה. עכשיו תתמקד בקטע בין שתי העשיריות שבו המספר נמצא ותחלק אותו ל-10 חלקים שווים. זה ייתן לך הספרה השנייה של המספר. אם ממשיכים בהליך הזה עד אינסוף מקבלים מספר בעל אינסוף ספרות עשרוניות שווה בדיוק למספר המבוקש. להוכחה פורמלית יותר תצטרך לעבוד עם הגדרת מספר ממשי בעזרת חתכי דדקינד או סדרות קושי, אבל בכל מקרה המסקנה זהה: לכל מספר ממשי יש ייצוג עשרוני. מה שכן, רוב המספרים הממשיים אינם חשיבים. כלומר אין שום אלגוריתם שפולט את כל ספרותיו בזו אחר זו. דניאל • תרמו ערך 14:01, 16 בנובמבר 2012 (IST)

זווית פיזור

איך מוגדרת זווית פיזור? בשרטוט שלי האם זה a או b. 79.182.225.36 15:49, 16 בנובמבר 2012 (IST)

ראה בערך פיזור. eman • שיחה • ♥ 15:53, 16 בנובמבר 2012 (IST)

טענה מוזרה במתמטיקה

חשבתי על איזו טענה טיפשית שאני לא יודע לקבוע אם היא נכונה או לא: "כל המספרים השלמים בין 1 ל2 (לא כולל קצוות) גדולים מ3".

מצד אחד, מספרים בין 1 ל2 לא יכולים להיות גדולים מ3. אבל מצד שני, אין שלמים בקטע שאני חוקר. אז האם הטענה הזאת נכונה? 79.181.207.147 11:37, 17 בנובמבר 2012 (IST)

נראה לי שהשאלה היא האם הטענה הזאת היא טענה. eman • שיחה • ♥ 11:57, 17 בנובמבר 2012 (IST)

למה לא? גם "כל הפילים יודעים לעוף" זאת טענה. 79.181.207.147 12:31, 17 בנובמבר 2012 (IST)

זה ממש לא אותו דבר. "כל הפילים יודעים לעוף" זאת טענה לא נכונה, אבל טענה. אם רוצים השוואה זה יהיה "כל הפילים שמטילים ביצים יודעים לעוף". כי אתה טוען טענה לגבי קבוצה שבהכרח היא ריקה. eman • שיחה • ♥ 12:46, 17 בנובמבר 2012 (IST)

זאת אכן טענה נכונה. לירן (שיחה,תרומות) 12:41, 17 בנובמבר 2012 (IST)

ראה נכון באופן ריק. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

חישוב שגיאות

אם הגודל מסוים הוא $A=0.5\pm 0.02$ אז מהיא השגיאה ב$B=1/A$? 79.181.207.147 12:33, 17 בנובמבר 2012 (IST)

הרעיון הוא שאם ידוע לך ערך של $x$ עד $\pm \Delta x$ ויש לך פונקציה שלו, אז ערכה ידוע עד כדי $\pm \Delta f=\pm \left|{\frac {df}{dx}}\right|\Delta x$ , כלומר במקרה שלנו $\Delta B=\Delta A/A^{2}$. eman • שיחה • ♥ 12:55, 17 בנובמבר 2012 (IST)

תודה. וקצת יותר קשה: יש לי A ושגיאה בA . יש B ושגיאה בB ואני רוצה לדעת מה השגיאה ב$C=A/B$. 79.181.207.147 13:22, 17 בנובמבר 2012 (IST)

זה יותר מסובך. בשלב הראשון אתה מחשב באותה דרך את התרומה מכל אחת מהשגיאות. בעקרון היה אפשר לחשוב שצריך פשוט לחבר את התרומות האלה. זה אפילו נכון בתנאים מסויימים. אבל בד"כ, אם אין תלות בין המשתנים השונים (ואז ייתכן ש A מקטין את הערך, אבל B דווקא מגדיל אותו) , מה שעושים זה לקחת את שורש סכום ריבועי התרומות. eman • שיחה • ♥ 13:47, 17 בנובמבר 2012 (IST)

מעולה. מה עושים במקרה של שורש? ${\sqrt {A}}$. להוציא שורש מהשגיאה של A? 79.181.207.147 15:35, 17 בנובמבר 2012 (IST)

לא. זה השגיאה של A חלקי פעמיים השורש של A. eman • שיחה • ♥ 18:08, 17 בנובמבר 2012 (IST)

קיבול חום

מחפש בכל העולם ולא מוצא: מהו קיבול חום בנפח קבוע $C_{v}$ של הגזים: הליום, חנקן ופחמן דו חמצני טמפרטורה 273 קלווין? התשובה הראשונה שתבוא היא בטח לחפש בHeat_capacity. אבל ברשימה שם יש רק בטמפרטורת החדר(לא מה שאני צריך). למי יש את המידע הזה? 79.179.187.153 17:05, 17 בנובמבר 2012 (IST)

סביר שאין שינוי משמעותי בקיבול החום בטווח הטמפ' הזה. 94.159.153.104 18:15, 17 בנובמבר 2012 (IST)

מדוע מקררים את שמשת הרכב לצורך הסרת אדים ומניעתם ביום קר?

האוויר הנפלט מגופנו ומנשימתנו הוא חם ולח, וכאשר השמשה קרה נוצרים אדים. אם נקרר אותה עוד יותר, יווצרו אדים ביתר קלות. בהנחה שלא מקררים את האוויר ברכב, אלא את השמשה בלבד, כיצד זה יכול לעזור? אביעד‏ • שיחה 19:29, 17 בנובמבר 2012 (IST)

אני לא יודע מה התשובה, אבל תדע לך שגם אם מפעילים את המזגן על חימום זה מעלים את האדים. בלנק - שיחה 20:14, 17 בנובמבר 2012 (IST)

קודם כל תיקון - מה שנוצר על החלון אלו טיפות מים ולא אדים. אדי מים הם שקופים ולא ניתן לראותם. גם הבל הנשימה ביום קר וערפל עשויים מטיפות מים ולא מאדים. ולשאלתך, האוויר היוצא מהמזגן הוא לא רק קר אלא בעיקר יבש והוא סופח אליו את המים מהשמשה ומייבש אותה בדומה למכשיר לייבוש ידיים. אם תפעיל את המזגן (בכפתור המסומן בדרך כלל ב-AC) ותכוון את הטמפרטורה לחימום, השמשה תתנקה יותר מהר. Easy n - שיחה 20:23, 17 בנובמבר 2012 (IST)

שיוויון

באילו מקרים משתמשים ב"= רגיל" ובאילו ב"= עם 3 פסים"( שווה זהותית). 79.176.252.227 20:16, 18 בנובמבר 2012 (IST)

כשיש שוויון עם משתנים ורוצים להדגיש שמדובר בשויוון לכל ערך של המשתנים (זהות) ולא רק להשמה ספיצפית. למשל $f(x)=1$ יכול לסמן משוואה (שפתרונותיה הם המספרים שייתנו לפונקציה את הערך 1) או בתור שוויון שנכון ל-x ספיציפי (שמוזכר במקום אחר בטקסט). למשל "קיים x כך ש-$f(x)=1$". לעומת זאת $f(x)\equiv 1$ מסמן שלכל ערך של x מתקבל הערך 1. כלומר f היא פונקציה קבועה. דניאל • תרמו ערך 20:40, 18 בנובמבר 2012 (IST)

בתחומי מדע מדויק כמו כימיה או פיזיקה משתמשים בשווה זהותית כשרוצים לומר "שווה, לפי הגדרה". 94.159.145.124 21:45, 18 בנובמבר 2012 (IST)

גם במתמטיקה. דניאל • תרמו ערך 23:22, 18 בנובמבר 2012 (IST)

פיתרון מד"ר אחת

המשוואה היא $yy''=1+y'$. איך פותרים אותה? אני יודע שהפיתרון אמור לצאת קוסינוס היפרבולי. 79.176.252.227 21:39, 18 בנובמבר 2012 (IST)

קוסינוס היפרבולי לא פותר את זה. התכוונת אולי ל-$yy''=1+(y')^{2}$? דניאל • תרמו ערך 23:38, 18 בנובמבר 2012 (IST)

נכון. איך פותרים אותה? 192.114.105.254 13:34, 19 בנובמבר 2012 (IST)

אפשר עם התמרת לפלס. ניסיתי ולא הצלחתי, כנראה שאני חלוד מדי. ליאור पॣ • ה' בכסלו ה'תשע"ג • 14:00, 19 בנובמבר 2012 (IST)

לא למדנו התמרות אינטגרליות. 192.114.105.254 15:06, 19 בנובמבר 2012 (IST)

גזור את שני האגפים לפי x. מכאן הפתרון די טריויאלי. בהצלחה.

תוכל לפרט? אני לא חובב משוואות דיפרנציאליות אבל אני לא רואה איך זה עוזר. יש אלגוריתם שעושה רדוקציה ממשוואה חסרה (x לא מופיע) מסדר שני למשוואה מסדר ראשון. כדאי למצוא אותו. בכל אופן עם קצת משחק הגעתי לזה:

$(\ln y)''=\left({\frac {y'}{y}}\right)'={\frac {yy''-(y')^{2}}{y^{2}}}={\frac {1}{y^{2}}}$. נסמן $\ln y=z$ ונקבל: $z''=e^{-2z}$ וזו משוואה שכבר פחות קשה לפתור. דניאל • תרמו ערך 19:38, 19 בנובמבר 2012 (IST)

בבקשה, נגזור את שני האגפים ונקבל $yy'''+y'y''=2y'y''$, או $yy'''=y'y''$. לאחר חלוקה מתקבל ${\frac {y'}{y}}={\frac {y'''}{y''}}$, כלומר, ${\frac {d}{dx}}\left(\ln y\right)={\frac {d}{dx}}\left(\ln y''\right)$, לכן $\ln y''=\ln y+c$, או $\ln {\frac {y''}{y}}=c\rightarrow y''=cy$. כל טוב.

תודה. משום מה פספסתי תג אחד בגזירה. צריך להיזהר ולשים לב שהגזירה ייצרה פתרונות שלא פתרו את המשוואה המקורית (למשל $e^{-x}$). דניאל • תרמו ערך 20:43, 19 בנובמבר 2012 (IST)

מעגל LC

אני רוצה לפתח את הזרם כפונקציה של הזמן במעגל LC. מצורף בזאת הפתרון שלי. הבעיה היא שהמד"ר שקיבלתי שונה מהמד"ר בערך מעגל תהודה חשמלי (שלי מסדר ראשון. שלכם מסדר שני!). אז אני לא בטוח שהפיתרון שלי נכון.

ועוד דבר, אני מתבקש לפתור את זה עם אויילר-לגרנג'. ואני לא לגמרי בטוח איך אני עושה את זה. 79.176.252.227 22:57, 18 בנובמבר 2012 (IST)

בדוק שאכן כתבת שם משהו. ראיתי דף ריק. בנצי - שיחה 01:28, 19 בנובמבר 2012 (IST)

בכל מקרה, משוואה מסדר ראשון מתקבלת עבור זרם כפונק' של הזמן. סדר שני מתקבל, כמו בערך אליו התייחסת, עבור מטען כפונק' של הזמן. בנצי - שיחה 03:01, 19 בנובמבר 2012 (IST)

לא. מה שלא עושים לו את המשוואה - מטען, זרם או מתח, תמיד צריכה להתקבל משוואה מסדר שני.

כשיש לך נגזרת ראשונה של הזרם לפי הזמן ומטען, זו משוואה מסדר שני (עבור המטען). לא מסדר ראשון. eman • שיחה • ♥ 03:50, 19 בנובמבר 2012 (IST)

יש לך שם טעות פיזיקלית בסיסית. זה לא שהאנרגיה בקבל שווה לאנרגיה במשרן. זה שסכום האנרגיות קבוע! אבל כמובן שלא ידוע מהו הקבוע הזה (שהוא האנרגיה הכוללת, שתלוי בתנאים של המערכת).

אז כותבים משוואה שסכום האנרגיות שווה קבוע, ואת המשוואה הזו גוזרים לפי הזמן, מצמצמים מה שצריך, ומקבלים את המשוואה הנכונה. eman • שיחה • ♥ 02:58, 19 בנובמבר 2012 (IST)

תודה לך EMAN. תיקנתי את היצירה שלי. אני רואה שיש בעיה עם מינוס (ואם אני עושה אופטימיזציה של E עם מינוס אז יוצא נכון). אני רק לא רואה את ההצדקה להוספת מינוס. 192.114.105.254 15:05, 19 בנובמבר 2012 (IST)

הבעיה היא ששמת במשוואה את האנרגיה הכוללת (שהיא סכום האנרגיות של המשרן והקבל), במקום את הלגראנז'יאן, שההוא ההפרש שלהן). eman • שיחה • ♥ 16:24, 19 בנובמבר 2012 (IST)

א. ניסיתי לעיין אתמול בדף שהעלית, אבל לא ניתן היה, ולכן ביקשתי שתבדוק זאת (בדיעבד התברר שהאתר שלהם היה עמוס מדי).

ב. איך 'הסתדרת' עם עניין סדר ראשון או שני ? בנצי - שיחה 20:29, 19 בנובמבר 2012 (IST)

הסתדרתי עם ההערה האחרונה של eman. הרעיון הוא להתייחס לC "כמסה מוכללת" ולאנריגה של סליל כ"קפיץ מוכלל" ואז לעשות ואריאציות עם אויילר לגרנג'. מדהים, אבל מקבלים אוסיצילור הרמוני קלאסי. 79.183.215.183 21:56, 19 בנובמבר 2012 (IST)

א. אכן, זהו אנלוג מושלם למתנד אידיאלי (ללא אובדני אנרגיה), רק שבמקרה זה האנרגיה מתגלגלת מאנרגיה פוטנציאלית חשמלית (בקבל) לאנרגיה האצורה בשדה המגנטי שהסליל יוצר (באנלוגיה לפוט' כובדית וקינטית).

ב. את השאלה השניה שאלתי, מאחר ושאלתך המקורית התייחסה לזרם כפונק' של הזמן, ומשוואה כזו צריכה להיות מסדר ראשון. בנצי - שיחה 22:23, 19 בנובמבר 2012 (IST)

הנגזרת השניה היא מאויילר-לגרנג'. 79.183.215.183 22:25, 19 בנובמבר 2012 (IST)

לפלסיאן

באונ' למדנו את הפתרון למשוואת שרדינגר בחד מימד, וכשרצינו לעבור לדו מימד או תלת מימד המרצה עבר אוטומטית מנגזרת שנייה ללפלסיאן. ממה נובע שכך צריך לעשות? תודה, 109.160.149.13 17:48, 19 בנובמבר 2012 (IST)

שאלתך לא לגמרי ברורה. אם אתה יודע מהו לפלסיאן, הרי שזהו אופרטור הנותן את סכום הנגזרות החלקיות לפי שיעורי המקום במישור או במרחב. זוהי בדיוק הנגזרת השניה, רק באופן הלוקח בחשבון את כל השינויים במרחב, ולא רק בממד אחד. בנצי - שיחה 23:38, 19 בנובמבר 2012 (IST)

אני מניח שהשאלה היא מדוע דווקא האופרטור הזה, ולא הנגזרת השניה לפי x או לפי y, או צירוף לינארי אחר של שתיהן. הסיבה היא שהלפלסיאן הוא התבנית הדיפרנציאלית השניה היחידה שאינה תלויה במערכת הצירים, כלומר שאינה משתנה תחת סיבוב של המערכת. עוזי ו. - שיחה 23:56, 19 בנובמבר 2012 (IST)

במכניקה קלאסית, ההמילטוניאן הוא ${\frac {p^{2}}{2m}}+U$. במימד אחד $p^{2}$ זה זה פשוט הריבוע של התנע p. אבל בשלושה מימדים $p^{2}=p_{x}^{2}+p_{y}^{2}+p_{z}^{2}$. ועכשיו תכליל את ההגדרה של אופרטור התנע הקווי (במסגרת הקוונטית) ממימד אחד לשלושה אופטורים עבור כל אחד מרכיבי התנע, תציב, ותקבל את הלפלסיאן. eman • שיחה • ♥ 02:37, 20 בנובמבר 2012 (IST)

תודה לכם. 94.159.135.238 19:58, 20 בנובמבר 2012 (IST)

חומצה הידרוכלורית

מספר שאלות על חומצה הידרוכלורית. 1. יש לי קופסה של חומצה הידרוכלורית וכתוב עליה כך: (א) זהירות חומצה! (במקרה של פגיעה יש לשטוף וכו') (ב) חומר למאכל (c). מה פשר האזהרה מחד והכיתוב 'חומר למאכל' מאידך?

כמו כן איזה ניסויים כימיים ביתיים מעניינים אפשר לעשות עם חומצה הידרוכלורית? 95.35.135.229 17:58, 19 בנובמבר 2012 (IST)

זו טעות חמורה. מדובר בחומר מאכל שיכול לגרום לנזק רב בשימוש לא נכון. חומצת מימן כלורי היא חומר מסוכן. אל תתעסק בחומרים שאינך יודע לטפל בהם או לא יודע מה לעשות במקרה חירום שבו החומר נשפך. טל (רונאלדיניו המלך) • שיחה 19:13, 19 בנובמבר 2012 (IST)

אסור לעשות ניסויים ביתיים עם חומצות חזקות. הדבר יכול לגרום לכוויות, להרס רכוש ובמקרים חמורים אף למוות. אם אתה רוצה לעשות ניסוי עם חומרים כימיים, הרשם למגמת כימיה בתיכון או לחוג לכימיה באונ'. גילגמש • שיחה • גם אני משתתף במיזם העשור! 05:57, 20 בנובמבר 2012 (IST)

אני בספק אם כל המדענים שביצעו ניסויים עשו אותם באוניברסיטה, רבים מהם חשפו תגליות בביתם על ידי ניסויים. ישנה קבוצה בעולם המעודדת ניסויים מעבדתיים בבית (הם מכונים 'טינקרים'. כתוב בגוגל "תרבות הטינקרים" וכנס לכתבה בויינט), נסה לברר איתם את הנושא. בכל אופן רצוי לעבוד רק עם הדרכת מוסמך. 176.13.132.182 01:28, 21 בנובמבר 2012 (IST)

מעלית הידראולית

האם נכון לומר כי במעלית הידראולית - היחס בין השטחים של כל צד פרופורציוני ליחס בין הגבהים שהבוכנות עולות/יורדות? אביעד‏ • שיחה 18:09, 19 בנובמבר 2012 (IST)

ביחס הפוך. עבוד לפי עקרון שימור נפח. ‏Setreset • שיחה 14:13, 20 בנובמבר 2012 (IST)

האם הטילים של החמאס עוברים את מהירות הקול?

קראתי שהטילים של החמאס למרכב נעים במהירות של 1500 קמ"ש! א. האם זה נכון? ב. האם הם עוברים את מהירות הקול? 95.35.135.229 18:27, 19 בנובמבר 2012 (IST)

בו נעשה חישוב נאיבי תוך הזנחת פרטים רבים. ידוע שלמי שגר 40 ק"מ מהרצועה יש דקה לתפוס מחסה בהישמע אזעקה. אז נניח שרקטה עוברת 40 ק"מ בדקה. זה אומר 2400 קמ"ש (הכפלתי ב-60). זו כמובן הערכה מופרזת כי היא מניחה שאנחנו שומעים אזעקה בשנייה שמשוגרת רקטה וסביר שפיקוד העורף לקח מרווח בטחון ונוקב בזמן של דקה כאשר בפועל מדובר ביותר (ומי שמאזין לפיצוצים אכן מבחין שמדובר ביותר מדקה). אבל אפילו אם הפרזנו והמהירות האמיתית קטנה פי 2, זו עדין מהירות ממוצעת גדולה יותר ממהירות הקול. דניאל • תרמו ערך 18:40, 19 בנובמבר 2012 (IST)

כתבתי לפני התנגשות עריכה:

מעזה לבאר שבע המרחק הוא כ-40 ק"מ. זמן התעופה הוא כדקה. אולי קצת יותר. בוא נניח שאפילו דקה וחצי. בשעה אחת (60 דקות) נכנסות 40 פרקי זמן של דקה וחצי\ לכן הטיל יעשה מהירות ממוצעת של כ-1600 קמ"ש (וזו רק מהירות אופקית ממוצעת). לכן הוא בהחלט עובר את מהירות הקול. אבל גם כל קליע של רובה עובר את מהירות הקול. eman • שיחה • ♥ 18:43, 19 בנובמבר 2012 (IST)

האם הם יוצרים "בום" על-קולי? 80.230.90.250 21:08, 19 בנובמבר 2012 (IST)

א. בעקרון, כן, אבל האם ראית את חרוט גל ההלם המהווה את ה'בום' ? עיין בבום על-קולי, ובאיור גל ההלם בפרט - גל הלם זה נוצר מאחורי כלי הטיס, ולכן כמעט ואינו מתפזר סמוך לפני הקרקע.

ב. שים לב לכך שמהירות הקול איננה גודל קבוע, והיא תלויה, בין היתר, בלחץ האויר. מסיבה זו אין מתייחסים סתם ל'מהירות קול', אלא למספר מאך. בנצי - שיחה 22:49, 19 בנובמבר 2012 (IST)

אימן צודק. 700 מטר לשנייה זה הרבה יותר מהר ממהירות הקול. אין שום סיבה לטרוח ולא לומר פשוט "מהירות הקול" כאשר ברור מן ההקשר למה הכוונה. ואם כבר טורחים, אז לדבר על מספר מאך (שהוא בכלל גדול חסר ממד שמשתנה בהתאם לתווך) לא פותר את העניין. דניאל • תרמו ערך 23:09, 19 בנובמבר 2012 (IST)

א. תודה על הערתך הראשונה. לא ברור לי איך התייחסתי לנתון זה שלו בצורה לא נכונה, ולכן היסרתי את הערתי שם. אין פה בכלל ויכוח, שהרי מהירות הקול היא דבר ידוע.

ב. לא ברורות לי שתי הערותיך בהמשך: "ברור מן ההקשר" ? "לא פותר את העניין" ? בנצי - שיחה 23:31, 19 בנובמבר 2012 (IST)

פליקס באומגרטנר קפץ מהקפסולה אל כדור הארץ. אם מישהו היה קופץ אחריו, בהפרש זמן מתאים, האם הוא היה שומע במשך כל זמן הנפילה את הבום העל-קולי שיצר באומגרטנר? 80.230.90.250 00:06, 20 בנובמבר 2012 (IST)

הוא עבר את מהירות הקול באזור בו האוויר מאוד מאוד דליל. לכן אין סיסה שייווצר בום על קולי, ואם כן, הוא יהיה חלש באופן משמעותי. eman • שיחה • ♥ 02:39, 20 בנובמבר 2012 (IST)

אבל אם הוא המשיך בנפילה חופשית, אז המהירות שלו נשארה גבוהה, גם כשהוא הגיע לאזור בו האוויר אינו דליל, ואז היה אמור להיווצר בום על קולי. 77.125.236.121 05:21, 20 בנובמבר 2012 (IST)

קודם כל חשוב להבין שהבום הוא לא כשהמהירות גדולה ממהירות הקול, אלא כשהיא משתווה לו. בעקרון אולי גם כשהוא משתווה בדרך למטה. אבל עדיין יכול להיות שזה היה באוויר מספיק דליל בשביל שהוא יהיה חלש. הוא אל עבר בהרבה את מהירות הקול. eman • שיחה • ♥ 09:19, 20 בנובמבר 2012 (IST)

לפי הערך בום על-קולי, עבור מטוס שטס בדיוק במהירות הקול, הבום יישמע מתחתיו, כלומר אדם שניצב על הקרקע ישמע את הבום ברגע שהוא יראה את המטוס חולף מעליו. עבור מטוס שמהירותו גבוהה יותר, הבום יישמע זמן קצר לאחר שהמטוס יעבור מעל לצופה. כלומר, גם מהירות גבוהה יותר ממהירות הקול יוצרת בום. 77.125.236.121 13:50, 20 בנובמבר 2012 (IST)

בום על קולי נוצר ברגע בו הגוף עובר את מהירות הקול. במקרה של קליע זה קורה בתוך הקנה. מאוד ייתכן שזה גם מה שקורה עם הטילים. ואז אני לא יודע האם באמת יש בום על קולי, אבל גם אם כן, הוא קרוב לוודאי חלק מקול הירי. eman • שיחה • ♥ 00:54, 20 בנובמבר 2012 (IST)

יש לי כמה שאלות (מבקש סליחה על אריכות הדברים):
(1) האם חפץ גדול שנע במהירות הקול גורם ל"בום" רועש יותר מאשר חפץ קטן שנע במהירות הקול?
(2) ברגע שהמטוס מגיע למהירות הקול, הוא נמצא בשפת חרוט גל ההלם. האם הטייס שומע את הבום שהוא עצמו יצר?
(3) האם חללית עוברת את מהירות הקול במהלך השיגור לחלל? (3ב) האם שומעים על הקרקע בום על קולי? (3ג) אם מהירות החללית עוברת את מהירות הקול, אז המהירות היחסית בינה ובין כדור הארץ היא גבוהה ממהירות הקול. האם האסטרונאוטים שומעים בום, שמקורו בתנועה היחסית של כדור הארץ ביחס לחללית?
(4) מטוס טס במהירות קבועה, שהיא גדולה או שווה למהירות הקול. אני נמצא על הקרקע בנקודה כלשהי. ברגע שאני שומע את הבום, אני מתחיל לנסוע במהירות על הקרקע, כך שאני נמצא כל הזמן בשפת חרוט גל ההלם. (נניח שלא עוצר אותי שוטר בדרך.) האם אני אשמע בום מתמשך, או שהבום נשמע רק בכניסה לחרוט גל ההלם וביציאה ממנו, ואילו מי שנמצא כל הזמן בשפת החרוט אינו שומע את הבום?
(5) לפי הכתוב בערך בום על-קולי, מהירות גבוהה מקטינה את זווית הפתיחה של חרוט גל ההלם. מהו היחס המדוייק בין זווית הפתיחה ובין המהירות?
(6) פליקס באומגרטנר צנח בנפילה חופשית ועבר את מהירות הקול. בגלל התאוצה, מהירות הצנחן אינה קבועה אלא הולכת וגדלה. האם במקום גל הלם שצורתו חרוט בעל ציר אופקי, מתקבל משטח דמוי חצוצרה בעל ציר אנכי?
(7) נניח, שצנחן נוסף קפץ t שניות אחרי פליקס באומגרטנר. מצד אחד, המרחק בין שני הצנחנים הולך וגדל בכל רגע, וגם ההפרש בין המהירויות שלהם הולך וגדל. מצד שני, גם הרדיוס של תחום גל ההלם (שכעת אינו בצורת חרוט) הולך וגדל. האם קיים ערך של t, עבורו הצנחן השני יימצא בשפת תחום גל ההלם במשך כל הנפילה?
(8) האם לשפת חרוט גל ההלם יש עובי חיובי? (8ב) במהירויות עצומות, חרוט גל ההלם נעשה צר מאוד. האם בסמוך למטוס, צד אחד של שפת החרוט משיק/חותך/מתלכד עם הצד השני?
(9) לפי הכתוב בערך מספר מאך, "במהירות מאך 1 החרוט נראה כקיר מכופף קלות לאחור בקצותיו", ולפי הכתוב בערך בום על-קולי תחת האיור השני, "מטוס שנע במהירות הקול יוצר גל הלם. צופה ישמע את הבום העל-קולי כאשר המטוס יחלוף מעליו". אבל, באיור של המטוס שנע במהירות הקול, לא מופיע קיר מכופף אלא מעגלים מקוננים זה בזה, ולפי האיור נראה, שהצופה שעל הקרקע ישמע את הבום אחרי שיחלוף פרק זמן כלשהו מרגע שהמטוס חלף מעליו. האם צריך להחליף את המעגלים שבאיור במעגלים ענקיים בעלי רדיוס אינסופי? 77.125.233.24 04:05, 21 בנובמבר 2012 (IST)

תשובה לשאלה (6) אם מתעלמים מכך שבאוויר דליל מהירות הקול היא איטית יותר מאשר באוויר צפוף, ואם מתעלמים מכך שבגובה רב קבוע הגרביטציה הוא קטן יותר מאשר בגובה נמוך, ואם מתעלמים מהחיכוך של הצנחן באוויר, אז שפת תחום גל ההלם היא בצורת משטח, שנוצר מסיבוב קשת של פרבולה, שקודקודה נמצא בגובה של הקפסולה (מיקום הקודקוד מתרחק מהקפסולה בכיוון אופקי), סביב הציר האנכי שעובר דרך הצנחן. אם אין מתעלמים מהשינויים בצפיפות האוויר ובקבוע הגרביטציה ומהחיכוך באוויר, אז המשטח שמתקבל יהיה דומה למשטח שהגדרנו, אבל הוא יהיה צר יותר בחלק העליון שלו, ורחב יותר בחלק התחתון.

טעות בשאלה (7) אם הצנחן השני קפץ מאותו מקום שהראשון קפץ ממנו, אז הוא יימצא בפנים של תחום גל ההלם, ולא בשפתו.

תיקון לשאלה (7) נניח, שצנחן נוסף קפץ t שניות אחרי פליקס באומגרטנר, מקפסולה אחרת, כאשר שתי הקפסולות נמצאות באותו גובה, והמרחק האופקי ביניהן הוא d. נניח, שלצנחן השני יש מהירות אופקית התחלתית v. אז הקו שבו הצנחן השני נע הוא בקירוב קשת של פרבולה. עבור אילו ערכים של t,d,v, קיים פרק זמן חיובי, שבו הצנחן השני נמצא בשפת תחום גל ההלם? 77.125.233.24 14:40, 21 בנובמבר 2012 (IST)

כוח סוס

במנוע השראה לפעמים נתון לי ההספק שלו בכוח סוס (HP) ולא בוואט. בערך האנגלי en:horsepower#Current definitions יש לי טבלת המרות לוואט. האם מישהו יודע איך ממירים לפי כ"ס חשמלי (1:746) או לפי כ"ס מטרי(1:735.5) או שמא לפי 1:745.7? -יונה בנדלאק - שיחה 15:45, 21 בנובמבר 2012 (IST)

מאחר ולכפול אתה יודע, מן הסתם, אני מניח ששאלתך היא באיזה יחס יש לבחור (זה לא ברור מאופן ניסוח השאלה). אם על כך שאלת, הרי שהדבר תלוי בארצו של יצרן המנוע. בארצות בהן נהוגה השיטה המטרית נהוג הערך השני שציינת (בקירוב), ואילו בחבר העמים הבריטי ובארה"ב, עדיין, נהוג הערך הראשון שאתה מציין. בנצי - שיחה 17:05, 21 בנובמבר 2012 (IST)

אכן זו שאלתי. איזה יחס לבחור. במקרה מקור השאלה הוא משרד החינוך הישראלי. במקרה זה מה צריך להיות היחס? -יונה בנדלאק - שיחה 18:01, 21 בנובמבר 2012 (IST)

בישראל נהוגה השיטה המטרית בכל, לכן נוהג בה הערך השני שציינת. בנצי - שיחה 18:50, 21 בנובמבר 2012 (IST)

האם הקפסולה שממנה קפץ לאחרונה פליקס באומגרטנר נשארה באוויר?

מה קרה לקפסולה שפליקס באומגרטנר קפץ ממנה, האם היא נשארה באוויר באותו מקום או מה? 109.253.67.183 17:25, 21 בנובמבר 2012 (IST)

כבר שאלו את זה כאן. אינני יודע ליצור קישור לפסקה המתאימה בדף הארכיון. 77.125.233.24 18:28, 21 בנובמבר 2012 (IST)

ראה בדף ויקיפדיה:הכה את המומחה/ארכיון199, בפסקה "קפיצה מחלל".

מישהו יודע איך ליצור קישור לפסקה המתאימה בדף הארכיון? 77.125.233.24 23:50, 21 בנובמבר 2012 (IST)

קישור 77.125.233.24 03:10, 22 בנובמבר 2012 (IST)

האם משפט פיתגורס הוא חוק פיזיקלי?

ישנה חוקיות מספרית ברורה בין כל המשולשים שאותם אני יכול למדוד, והחוקיות הזאת היא משפט פיתגורס. האם זה אומר שמשפט זה הוא חוק פיזיקלי, כמו חוקי ניוטון וקפלר? מצד אחד, מתמטיקאי יגיד שמה שאני מדדתי זה לא משולש מבחינה מתמטית טהורה, אלא איזשהו גוף שקירבתי למשולש. אבל מצד שני, כמו בכל ניסוי, יש תיאוריה ויש תוצאות. ותמיד יש הפרש בין הערך הנמדד לערך התאורטי. אז אני אומר שמשפט פיתגורס הוא המודל התאורטי והמדידות שלי הם הניסוי ואני קובע שיש התאמה בין תיאוריה לניסוי כי אטה יצא קטן מ-0.7 כלומר הוכחתי חוק מתמטי כחוק טבע? 79.181.227.74 20:40, 21 בנובמבר 2012 (IST)

לא, 'חוקיות מספרית' איננה חוק פיזיקלי אלא חוק או כלל או קשר מתימטי, משום שאינו מתייחס לגופים בפועל, אלא לקשר בין קטעים על ישרים מצטלבים, שהם ישויות תיאורטיות, רעיוניות בלבד. אמנם גופים ממשיים שאורכם מקיים את הקשר הם גופים פיזיים, אבל אז השימוש בכלל הוא יישום של חוק מתימטי בלבד, ולא חוק פיזיקלי בעצמו. כדי לדבר על חוק פיזיקלי, צריך שיהיה קשר של גורם או סיבה ותוצאה בין הישויות הפיזיקליות הנדונות, או בצורת מודלים מופשטים שלהם. גם קשרים כאלה, בהרבה מקרים, מתוארים ע"י קשרים מתימטיים או בשפה מתימטית, אבל הם מתארים קשרים פיזיקליים או חוקיות פיזיקלית. בנצי - שיחה 22:59, 21 בנובמבר 2012 (IST)

הכרעת צדק בשאלת אחוזים אלגברית

השאלה כזו: מחירו המקורי של אופנוע היה X שקלים. האופנוע התייקר ב-20% ולאחר מכן הוזל המחיר ב-20%. הבע באמצעות X את מחיר האופנוע לאחר שני השינויים האלה (ההתיקרות וההוזלה). התשובה שלי היא 0.24X מהסיבה הפשוטה: ההתיקרות הראשונה גרמה לאופנוע לעלות 1.2X (כי 120 לחלק ל-100 שווה 1.2). כעת, לאחר ההוזלה של 20% (מהמחיר הסופי), מחלקים את המחיר שלאחר ההתיקרות (המחיר הסופי) לחמש חלקים (כי 100 לחלק ל-20 שווה 5), כלומר 1.2X לחלק ל-5 וזה יוצא 0.24X

התשובה בחוברת היא 0.96X. מי משנינו צודק? 95.35.149.154 00:18, 22 בנובמבר 2012 (IST)

התשובה בחוברת היא הנכונה. כאשר אומרים "המחיר הוזל ב-20%", מתכוונים לכך, שמחיר המוצר אחרי ההוזלה קטן ב-20% ממחירו לפני ההוזלה. כלומר, מחירו אחרי ההוזלה שווה ל-80% ממחירו לפני ההוזלה. לפי נתוני השאלה, המחיר המקורי היה X שקלים. אחרי ההתייקרות המחיר היה 1.2X שקלים. כעת, אחרי ההוזלה המחיר הוא 80% מתוך 1.2X, כלומר 0.8 כפול 1.2X, שזה 0.96X שקלים. 77.125.233.24 00:44, 22 בנובמבר 2012 (IST)

פשוט הפעל את אותה גישה שהפעלת בחישוב הראשון, גם בשני. בנצי - שיחה 00:49, 22 בנובמבר 2012 (IST)

תודה לשניכם על העזרה. 95.35.149.154 06:39, 22 בנובמבר 2012 (IST)

פרדוקס התאומים

ניקח גרסה כזאת:

2 שעונים איציק ובני מסונכרנים על פני כדור הארץ. איציק נשאר על כה"א וזורק את בני גבוהה לחלל. בני עולה לגובה מקסימום ונופל חופשית על איציק. מי יהיה זקן יותר ברגע המפגש? שימו לב, בני לא הפעיל מנועים בשום שלב של הניסוי. 192.114.105.254 13:09, 22 בנובמבר 2012 (IST)

שאלה מעניינת, שבשביל לענות עליה צריך לדעת הייטב יחסות כללית. רק כדאי לסנכרן את השעונים מייד אחרי הזריקה. 13:18, 22 בנובמבר 2012 (IST)

אני יודע מעט, אבל יודע( לא מריכולים). 79.181.227.74 18:30, 22 בנובמבר 2012 (IST)

קיום הוכחה לטענה

ממה שהבנתי, משפט אי-השלמות של גדל מוכיח שקיימת איזו טענה איזוטרית ולא מעניינת במיוחד שאינה ניתנת להוכחה/הפרכה. אבל מה ידוע על ההוכחה/הפרכה של טענות "אמיתיות"? האם לדוגמה השערת קולץ, במידה והיא נכונה, בהכרח ניתנת להוכחה? 212.76.109.218 14:25, 22 בנובמבר 2012 (IST)

ראשית הבה נדייק במה שגדל אמר. הוא לא אמר שהיא לא ניתנת להוכחה/הפרכה, אלא אמר כי: עבור כל מערכת מתמטית של אכסיומות (שאינן סותרות את עצמן, ושניתנות לזיהוי מכאני - למשל ע"י מחשב), ניתן לנסח בשפתה של המערכת איזושהי טענה - שאותה לא יהיה ניתן להוכיח/להפריך מתוך האכסיומות של המערכת (אגב הבאתי כאן את הניסוח היותר שלם של תגליתו של גדל, כפי שנוסח ע"י רוסר). אבל גדל מעולם לא רמז שהטענה הבלתי מוכחת והבלתי מופרכת הזאת חייבת להיות "איזוטרית ולא מעניינת במיוחד", ולכן כמובן שיתכנו גם טענות מאד מעניינות אשר לא יהיה ניתן להוכיחן (ואף לא להפריכן) מתוך המערכת. אם כי יש לזכור שבהכרח כן יהיה ניתן להוכיחן מתוך מערכת מתמטית אחרת של אקסיומות (שאינן סותרות את עצמן ושניתנות לזיהוי מכאני), למשל מערכת "חדשה" כזו שבה הטענה הנ"ל תהיה אחת מהאקסיומות של המערכת החדשה; החידוש שבדברי גדל הוא אפוא, במילים הקריטיות "כל מערכת" שבתחילת דבריו; מה שאומר, שדבריו נכונים גם לגבי המערכת "החדשה" הנ"ל! כלומר, גם עבור המערכת החדשה הנ"ל יהיה ניתן לנסח בשפתה איזושהי טענה (אם כי כמובן שונה מזו הקודמת) שאותה לא יהיה ניתן להוכיח/להפריך מתוך האכסיומות של המערכת החדשה; וחוזר חלילה, לגבי כל מערכת מתמטית של אכסיומות (שאינן סותרות את עצמן ושניתנות לזיהוי מכאני). אגב, במערכת "מתמטית" אני מתכוון למערכת שמניחה את האקסיומות של פעולת החיבור ושל פעולת הכפל. סמי20 - שיחה 15:03, 22 בנובמבר 2012 (IST)

יש טענות חשובות ומעניינות מאד שאי אפשר להוכיח או להפריך במסגרת תורת הקבוצות הסטנדרטית: הדוגמאות הבולטות ביותר הן אקסיומת הבחירה והשערת הרצף. עוזי ו. - שיחה 15:05, 22 בנובמבר 2012 (IST)

אגב, הדוגמה הכי מפורסמת והכי קדומה היא כנראה אכסיומת המקבילים, שאינה ניתנת להוכחה/להפרכה מתוך הגיאומטריה האוקלידית. סמי20 - שיחה 15:11, 22 בנובמבר 2012 (IST)

אוקיי. אז נשאל ככה: האם במערכת האקסיומות המקובלת היום למערכת המספרים ישנן טענות שאיננו יודעים כיצד להוכיחן, אך אנחנו יודעים שקיימת להן הוכחה? (הכיוון הכללי שלי הוא שבמערכת המספרים יש טענות שברור שהן נכונות או לא נכונות {השערת קולץ לדוגמה} ואני רוצה לדעת האם בהכרח יש להן הוכחה/הפרכה) 95.86.77.207 15:34, 22 בנובמבר 2012 (IST)

מה פירוש "אנחנו יודעים שקיימת להן הוכחה"? הוכחה באיזו מערכת? יש טענות על מספרים, כגון זו שהציג גדל, אשר מחד גיסא הן בלתי תלויות במערכת האקסיומות המקובלת של החשבון - מה שנקרא "מערכת פיאנו", אבל הן כן ניתנות להוכחה מתוך מערכת חשבונית רחבה יותר: כזו המכילה לא רק את מערכת פיאנו, אלא גם אותן - בתור אכסיומות נוספות של המערכת החדשה הנ"ל. ואגב, הן ניתנות *להפרכה* במערכת חשבונית *חדשה אחרת*: כזו המכילה לא רק את מערכת פיאנו, אלא גם את שלילתן - בתור אכסיומה נוספת של המערכת החדשה הנ"ל. עליך להבהיר אפוא אל מה אתה מתכוון ב"אנחנו יודעים שקיימת להן הוכחה". סמי20 - שיחה 15:54, 22 בנובמבר 2012 (IST)

אם אתה אומר שמערכת פיאנו היא המקובלת היום, אני מניח שהיא כוללת כל טענה שנכונה באינטואיציה (אמנם זה לא ניתן להוכחה מתמטית כמובן, אך בהתחשב בעובדה שגדולי המוחות עסקו בכך סביר להניח שהם לא פספסו דבר) האם הוכיחו משהו על קבוצת המשפטים המתקבלים ממנה?

(המוטיבציה לשאלה היא שקראתי איפשהו שהגאומטריה האוקלידית היא שלמה, כלומר כל טענה בה ניתנת להוכחה. אמנם מערכת המספרים לא יכולה להיות שלמה, אך אם הוכיחו שם שכל טענה נכונה היא גם יכיחה, אני סקרן לדעת האם משהו דומה קורה גם במערכת המספרים (שם יש בברור טענות שהן נכונות/לא נכונות במובן האינטואיטיבי של המילה)) 212.76.121.20 16:12, 22 בנובמבר 2012 (IST)

כבר הוכח שמשפט גודשטיין למשל (המכיל רק את פעולות החיבור-והכפל ומתייחס למספרים טבעיים בלבד), אינו ניתן להוכחה מתוך מערכת פיאנו (שהיא מערכת האקסיומות המקובלות של פעולות החיבור-והכפל שבין מספרים טבעיים), אבל הוא כן ניתן להוכחה מתוך תורת הקבוצות (שכמובן גם היא לא שלמה). אותו דבר הוכח לגבי משפט רֵמְזִי הסופי החזק, משפט העץ של קרוסקאל, ומשפט קאנאמורי-מקאלון. סמי20 - שיחה 16:31, 22 בנובמבר 2012 (IST)

תורת היחסות הכללית

השאלה כאן

לפי מה שהבנתי התשובה ב2.1 היא : שעון A עובר במערכת B מרחק של 2H ( את H ניתן למצוא) בזמן Tb ולכן אם $S=n\cdot 2H$ אז $C=S/Tb$. נכון?

ואיך אני עושה את סעיף 2.2? ההפרש בין Ta לTb הוא מסדר גודל של 10 בחזקת מינוס 14. אז יוצאת בערך אותה תשובה כמו קודם, עם הבדל שאי אפשר לחשב. 2 השאלות בהמשך, פשוט לא יודע. רק בבקשה לענות רק אם אתם יודעים קצת יחסות כללית.79.176.246.70 19:33, 22 בנובמבר 2012 (IST)

לחץ בבלון

מה הלחץ בבלון (העשוי גומי). 109.67.227.209 20:44, 22 בנובמבר 2012 (IST)

זה תלוי ברדיוסו ובחומר ממנו הוא עשוי. eman • שיחה • ♥ 21:19, 22 בנובמבר 2012 (IST)

תן מספר. נגיד בלון קטן שילד מנפח בפיו ליום הולדת. 109.67.227.209 21:44, 22 בנובמבר 2012 (IST)

לקפוץ מחללית

אסטרונאוט שעובד באחד הלוויינים יכול לקפוץ לכדור הארץ? נגיד אם החליפה ההיא ומצנח (כמו הבחור שקפץ מקצה האטמוספרה). אם אסטרונאוט יוצא מהחללית ומאבד איתה מגע פיזי- האם הוא יתחיל להאיץ לעבר כדור הארץ( אני יודע שהוא בנפילה חופשית, השאלה היא האם המרחק בינו לבין כדור הארץ ילך ויקטן בתאוצה או לא)?

אסטרונאוט יכול "לשחות" בנפילה חופשית לכיוון כ"א ואז ברגע הנכון לפתוח מצנח ולנחות? 79.183.203.103 12:01, 23 בנובמבר 2012 (IST)

סביר להניח שהוא יסחף לכיוון השמש ולא לכיוון כדור הארץ. -יונה בנדלאק - שיחה 12:03, 23 בנובמבר 2012 (IST)

מאוד לא סביר. תשעה חישוב קל ותמצא מה הכוח שמפעילה השמש על 80 קילו במרחק של AU אחת. תשווה זאת לכוחות אחרים. 79.183.203.103 13:02, 23 בנובמבר 2012 (IST)

לא ממש. בשביל "לשחות" הוא צריך תווך שנגדו הוא יכול להפעיל כוח.

לכן מה שייקרה זה שהוא ימשיך לנוע במסלול שדומה למסלול החללית. eman • שיחה • ♥ 12:08, 23 בנובמבר 2012 (IST)

רגע, זה אומר שאסטרונאוט לא מסוגל לנוע בחלל הפתוח בכלל? כלמור אין סכנה שתעוף לאיפשהו ביציאה מחללית ואתה תהיה איתה באותה המערכת בכל פנים?

אז ניקח שיטה אחרת- אסטרונאוט יוצא עם משוקלת כבדה ביד, זורק אותה החוצה מכדור הארץ ולכן משימור תנע יתחיל לנוע לכיוונה. 79.183.203.103 13:02, 23 בנובמבר 2012 (IST)

בעקרון הוא יכול לעשות את זה (דווקא עדיף שהוא ייזרוק אותה נגד כיוון התנועה שלו, בשביל שהמהירות שלו תהיה יותר איטית). השאלה היא האם זה יכול לתת לו מספיק מהירות (יחסית למהירות שיש לו במסלול) בשביל שהמסלול שלו יביא אותו לכדה"א מספיק מהר. eman • שיחה • ♥ 13:09, 23 בנובמבר 2012 (IST)

הוא ימות בכניסה לאטמוספירה. מהירות מסלולית היא כה גבוהה, שמה שהאסטרונאוט מסוגל להוריד ממנה בכח עצמו לא יהיה די על מנת למנוע את הפיכתו לכדור אש יפיפה. הפיקנופודיה טובה ממך! אילן שמעוני, - שיחה 13:31, 24 בנובמבר 2012 (IST)

למרבה הטרגדיה, זה כבר קרה, אם כי לא בקפיצה אלא נזרקו החוצה. לא חללית דווקא, אלא מעבורת. שתיים. בנצי - שיחה 23:05, 24 בנובמבר 2012 (IST)

מה הם הכללים האלמנטריים באופטיקה?

אני מנסה ללמוד אופטיקה (כחלק מלימוד פיזיקה) ומטבעי מאוד קשה לי לקבל כל מיני אקסיומות בלי נראות או מוכחות בדרך שוות ראיה, ולכן אשמח לקבל עצות שיקלו עלי בלימודי הפיזיקה בכלל (במיוחד לאור הרקע שממנו אני בא). כמו כן, אשמח לקבל רשימת כללים או עקרונות קונבנציונליים (המוסכמים על הכל) שאמורים להיות נר לרגלי ויסייעו לי בהבנת כל תורת האופטיקה. אני כרגע ממש בהתחלה, ואשמח לקבל דברים אלמנטריים ביותר. אני יודע שבאזור זה של הכה את המומחה מסתובבים מדענים דגולים שמאחוריהם נסיון רב עם כל המשתמע מכך, ומן הסתם יש ערך רב לתשובותיהם. תודה. מוטיבציה - שיחה 14:41, 23 בנובמבר 2012 (IST)

א. רואים את ההערכה שלך גם מבלי להפוך אותנו ל'מדענים דגולים'. גם הסקרנות שלך היא משהו הראוי להערכה.

ב. שאלת יותר מדי - מעין 'כל התורה כולה על רגל אחת', ואולי, במקרה זה, אצבע. אתה חייב להיות ספציפי ולחדד את שאלותיך. זו אינה רק הנחייה רצויה למקרה זה, אלא הנחייה כללית מומלצת - פיתוח היכולת להגדיר בעיה או נקודה לא מובנת. אני מציע שתתחיל ב'אקסיומות' עליהן אתה מדבר, וננסה לברר אותן יחד.

ג. אתייחס עתה לשני דברים: 1. מבט כללי על אופטיקה, ו-2. כמה תופעות יסוד, כולל הנחת קווים ישרים. תוכל להתייחס לתופעות יסוד אלה כאל פלטפורמה לשאלות שלך או לשאלות נוספות. תחום האופטיקה מורכב מכמה תת-תחומים שהוגדרו עפ"י הקשר. מדברים על אופטיקה גיאומטרית: אופטיקה העוסקת בהתפשטות האור מנקודה אחת (מקור) לנקודה שניה (יעד או מטרה), הן בתווך אחיד והן במעבר מתווך אחד לתווך שני. כל עוד התווך אחיד, (קרני) האור נעים בקווים ישרים לכל הכיוונים (גלי אור עם כיוון ומופע אקראיים, אבל זה יובן יותר בהמשך). לכן תחום זה מכונה 'גיאומטרית'. תוך כדי התפשטות האור בתווך, מתרחשת גם תופעה נוספת: בליעה, הנובעת מאינטראקציה של האור (שהוא סוג של קרינה א"מ) עם החומר ממנו מורכב התווך (תופעה זו מקבלת את הטיפול היסודי שלה במסגרת תת-התחום השלישי). במעבר מתווך לתווך, קורות, עקרונית, שתי תופעות: החזרה ו-שבירה, המצייתות לחוקי ההחזרה ולחוק סנל, בהתאמה. היסטורית, חוקים אלה אמפיריים, אבל הבסיס התיאורטי שלהם, שהתברר בדיעבד, מגיע ממשוואות מקסוול. סקרתי כאן, בקצרה, את תת-התחום הראשון. שני האחרים הם: אופטיקה פיזיקלית (דנה באופיו הגלי של האור, ותופעות הנובעות ממנו, דוגמת התאבכות, ובתופעות מעבר דרך חללים או עצמים שגודלם הוא מסדר-הגודל של אורך-הגל הרלוונטי, דוגמת עקיפה; ואופטיקה קוונטית, העוסקת בתופעות הנובעות מאופיו החלקיקי של האור, ובאינטראקציה בינו לבין חלקיקים, של חומר ואחרים). רצוי להתמקד קודם בראשון, מבלי להתפזר יותר מדי, ומכאן - לשאלות שלך. שבת שלום, בנצי - שיחה 16:25, 23 בנובמבר 2012 (IST)

קבוע קצב התגובה

שאלה בכימיה בדף זה. נגיד וחישבתי את כמות ההתנגשויות הממוצע בשניה. איך מכך אני מסיק את קבוע קצב של התגובה? כל מה שיש לי זה את ריכוז יוד והליום. 79.180.247.60 20:44, 23 בנובמבר 2012 (IST)

אם כל ההתנגשויות מובילות לתגובה, קצב התגובה (=קצב יצירת תוצר או העלמות מגיב) שווה לקצב ההתנגשויות (אמנם כל התנגשות יוצרת שתי מולקולות תוצר, אבל קצב התגובה מוגדר כך שמחלקים את קצב יצירת התוצר במקדם הסטוכיומטרי, כדי שהקצב יהיה קבוע בין אם מחשבים אותו לפי יצירת תוצר ובין אם לפי העלמות כל אחד מהמגיבים). קבוע הקצב הוא מספר שכשמכפילים אותו בריכוזי החומרים (בחזקות המתאימות) מקבלים את הקצב, לכן במקרה זה הקבוע שווה לקצב ההתנגשויות חלקי מכפלת ריכוזי המגיבים. 94.159.165.96 18:14, 24 בנובמבר 2012 (IST)

מכפלה וקטורית. טנזור לווי-צ'יווטה

מקור השאלה. הוכחתי את 2 הראשונים בכוח גס. 3 ממש קל (עושים דטרמיננטה ורואים 2 שורות תלויות). אבל 4 ו5 לא הולך בכוח גס (יוצא יותר מדי איברים). ולכן צריך איזו התחכמות פה, שכנראה קשורה לסעיפים הקודמים. למישהו יש רעיון איך לקשר בין ה"קרוס" לבין טנזור לווי-צ'יוויטה? 79.179.213.192 12:09, 24 בנובמבר 2012 (IST)

כן. הרעיון הוא שתשתמש בזה. קשר בין הדברים תמצא כאן. eman • שיחה • ♥ 12:15, 24 בנובמבר 2012 (IST)

כל מה שהגעתי אליו זה לרשום את המכפלה הסקלרית כ

${\begin{aligned}&{{V}_{i}}={{(B\times C)}_{i}}=\sum \limits _{j=1}^{3}{\sum \limits _{k=1}^{3}{{{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{k}}}}={{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{k}}\\&{{V}_{k}}={{(B\times C)}_{k}}=-\sum \limits _{j=1}^{3}{\sum \limits _{i=1}^{3}{{{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{i}}}}={{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{i}}\\\end{aligned}}$ (הסכם הסכימה של איינשטיין). לא בטוח במעבר האחרון, אבל נראה לי הגיוני זה זה החלפה אי זוגית.

אני מנסה לחשב את המכפלה הסלקרית המשולשת: ${{U}_{i}}=A\times {{(B\times C)}_{i}}=\sum \limits _{j=1}^{3}{\sum \limits _{k=1}^{3}{{{\varepsilon }_{ijk}}{{A}_{j}}{{(B\times C)}_{k}}}}={{\varepsilon }_{ijk}}{{A}_{j}}{{(B\times C)}_{k}}={{\varepsilon }_{ijk}}{{A}_{j}}{{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{i}}$

אני רוצה שזה היה דומה לזהות 2. אבל זה לא ממש. מה הבעיה שלי? 79.182.206.253 16:00, 24 בנובמבר 2012 (IST)

אתה משתמש באותם אינדקסי סכימה (dumb) פעמיים. אגב, זו לא מכפלה סקלרית (משולשת..). ירון • שיחה 17:52, 24 בנובמבר 2012 (IST)

התכוונתי וקטורית משולשת. איך אני עושה נכון עם האינדקסים? 109.67.247.127 18:00, 24 בנובמבר 2012 (IST)

ראה טנזור לוי-צ'יויטה ובפרט את הזהות השימושית $\sum _{i=1}^{3}\epsilon _{ijk}\epsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}$. בקשר לאינדקסים: אינדקס יכול להופיע במכפלה לכל היותר פעמיים, ואז סוכמים עליו. כאשר הוא מופיע פעם אחת הוא חופשי. אם הוא מופיע 3 פעמים באותו גורם סימן שכנראה עשית משהו לא נכון ויש להשתמש ביותר אותיות לאינדקסים (אם נגמרות לך האותיות באנגלית יש תמיד אותיות ביוונית ). בברכה, MathKnight (שיחה) 18:02, 24 בנובמבר 2012 (IST)

אני יודע מהו הסכם הסכימה. השתמשתי בו לפני כן (ראה את 2 השורות הראשונות). אז אם אני מחליף אינדקסים יוצא ${\begin{aligned}&{{U}_{a}}=A\times {{(B\times C)}_{a}}=\sum \limits _{b=1}^{3}{\sum \limits _{k=1}^{3}{{{\varepsilon }_{abc}}{{A}_{b}}{{(B\times C)}_{k}}}}={{\varepsilon }_{abk}}{{A}_{b}}{{(B\times C)}_{k}}={{\varepsilon }_{abk}}{{A}_{b}}{{\varepsilon }_{ijk}}{{B}_{j}}{{C}_{i}}\\&={{A}_{b}}{{B}_{j}}{{C}_{i}}({{\delta }_{ip}}{{\delta }_{jq}}-{{\delta }_{iq}}{{\delta }_{jp}})\\\end{aligned}}$

זה לא ממש מה שצריך להוכיח. 79.182.245.119 18:24, 24 בנובמבר 2012 (IST)

אתה מתבלבל באינדקסים. הזהות ש-Mathknight הציג כאן מועילה מאוד. ירון • שיחה 22:24, 24 בנובמבר 2012 (IST)

מד"ר

אני חלוד מאוד במד"ר (פעם ידעתי). איך פותרים את המשוואה: ${\ddot {\theta }}+{\frac {g}{l}}\theta ={\frac {A{{\omega }^{2}}}{l}}\sin(\omega t)$. אני זוכר שצריך לחלק לחלק הומוגני ופיתרון פרטי. החלק ההומוגני יוצא סינוס פלוס קוסינוס (עם כל הקובעים). איך אני מוצא את הפיתרון הפרטי להומוגנית? 79.182.196.201 15:12, 24 בנובמבר 2012 (IST)

מנחש!

במקרה הזה מנחש כמשהו מהצורה $y_{p}=A\cos(\omega t)+B\sin(\omega t)$ מציב במשוואה, ומוצא מהם A ו B.

ואגב, בד"כ יותר נוח לעשות את זה בצורה מרוכבת. כלומר לכתוב את המשוואה כחלק הממשי (או המדומה) ממשוואה אחרת מרוכבת, לפתור אותה, ואז לקחת בחזרה את מה שצריך מהפתרון. אבל אם זה מסובך, אפשר לעשות כמו שהצעתי בהתחלה. eman • שיחה • ♥ 15:16, 24 בנובמבר 2012 (IST)

מחפש דרך הגיונית לזכור סינוס של ארקוסינוס וכו'

האם יש דרך טובה לזכור את arcsin(cosX), או את arcos(sinX) וכו'? אביעד‏ • שיחה 19:43, 24 בנובמבר 2012 (IST)

"סינוס של ארקוסינוס" של איקס (כפי שניסחת זאת בכותרת שאלתך), הוא השורש הריבועי של ההפרש שבין אחד לבין הריבוע של איקס. ההיגיון הוא כמובן משפט פיתגורס. אבל שים לב שבתוכן שאלתך לא ניסחת את כותרת שאלתך. על כל פנים, עוזי העוקב לי מנסה לענות לך על תוכן שאלתך (שכאמור אינה מנסחת נכונה את כותרת שאלתך). אז אל מה באמת התכוונת? האם לכותרת שאלתך או שמא לתוכן שאלתך (או אולי לשניהם)? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

מספיק לזכור את ההגדרות: $y=\arcsin(\cos(x))$ כאשר $\sin(y)=\cos(x)$, כלומר $\ x+y={\frac {\pi }{2}}$. עוזי ו. - שיחה 20:43, 24 בנובמבר 2012 (IST)

לא ממש הבנתי למה זה מספיק. אם קיים $y=\arcsin(\cos(x))$ זה מחייב ש-$\sin(y)=\cos(x)$?

מן הסתם. זו ההגדרה של ארקסינוס. דניאל • תרמו ערך 00:45, 3 בדצמבר 2012 (IST)

מספר התנגשויות ביחידת זמן(קינטיקה של גזים)

נתון שבתנור בטמפרטורה קבועה של $773K$ ולחץ נתון של $800torr$ מצויים אטומי צזיום. מהו מספר התנגשויות לשניה?

אני לא יודע איך אני פותר את זה. יש לי את הנוסחה מספר ההתנגשויות ביחידת זמן (שנייה) ${{Z}_{AA}}=\sigma \cdot \left\langle {{v}_{rel}}\right\rangle {{N}_{A}}$. אבל הנוסחה רלוונטית אם ידוע לי ${N}_{A}$- מספר חלקיקים ליחידת נפח. ולפי ההגיון הוסחה הנ"ל היא גם לא בדיוק מה שאני צריך. כי ביקשו את מספר ההתנגשויות של אטום צזיום אחד בשנייה, לא את מספר ההתנגשויות של כל אטומי הצזיום בנפח מסויים בשנייה. 79.181.188.149 16:27, 25 בנובמבר 2012 (IST)

שאלת המשך: באותם תנאים של לחץ וטמפרטורה יש בכלי מספר שווה של אטומי צזיום ואשלגן. מהו $Z_{K,Cs}$? 79.181.188.149 16:54, 25 בנובמבר 2012 (IST)

אם ידועים לך הלחץ והטמפרטורה, ידועה לך גם הצפיפות המספרית (n/v), לפי משוואת הגז האידיאלי. אגב, ${{N}_{A}}$ זה מספר אבוגדרו, צפיפות מספרית מסמנים בד"כ ב-N סתם. 94.159.134.246 22:51, 25 בנובמבר 2012 (IST)

מה זה G המופיע על המחטים?

על המחטים של הזריקות כתוב שהקוטר(?) שלהם הוא 21G או 14G מה זה אומר? 194.114.146.227 11:30, 26 בנובמבר 2012 (IST)

לפי הערך באנגלית G הוא קיצור של מערכת המדידה Stubs Iron Wire Gauge שמשמשת למדידת צינורות וגופים גליליים. ברפואה, השימוש הוא בהקשר של מחטים ומסמל את הקוטר החיצוני של המחט. במקרים מסוימים יש משמעות גם לאורך המחט ולעובי שלה. טל (רונאלדיניו המלך) • שיחה 12:59, 26 בנובמבר 2012 (IST)

המספר מציין כמה מלאכים יושבים על חוד המחט והאות G מציינת את האורביטל של המלאך האחרון. ליאור पॣ • י"ב בכסלו ה'תשע"ג • 14:40, 26 בנובמבר 2012 (IST)

מלאכים?! מה הם שייכים לנדון? 176.13.239.122 20:43, 26 בנובמבר 2012 (IST)

ראה How many angels can dance on the head of a pin? כמובן שאין שקילות בין השאלה הנדונה לבין השאלה שבקישור. ליאור पॣ • י"ג בכסלו ה'תשע"ג • 21:46, 26 בנובמבר 2012 (IST)

שגיאה של ממוצע

יש שגיאה בגודל A ושגיאה בגודל B ועושים להם ממוצע. מה השגיאה בחישוב הממוצע? 109.65.214.70 22:34, 26 בנובמבר 2012 (IST)

האם ידוע לך למה הכוונה בניסוח "שגיאה בגודל A"? עוזי ו. - שיחה 22:46, 26 בנובמבר 2012 (IST)

כתוב את הממוצע כפונקציה של A ו B, ומצא את השגיאה על הממוצע בנגזרות חלקיות לפי A ו B. משה פרידמן - שיחה 22:47, 26 בנובמבר 2012 (IST)

מה נגזרות חלקיות? מדדתי ערך A וקיבלתי ניגד 5 פלוס מינוס 0.2. מדדתי B וקיבלתי 6 פלוס מינוס 0.5 למה שווה הממוצע של A וB והשגיאה בו? 109.65.214.70 23:00, 26 בנובמבר 2012 (IST)

אם המטרה היא פתרון תרגיל בית, אז כדאי להשתמש בנוסחאות שנתן המורה\המרצה. אם ברצונך לפתור בעיה אמיתית, אז בדוגמה שנתת הממוצעים יוצאים מחוץ לתחום השגיאה זה של זה. במקרה כזה הייתי אומר שהמדידות לא מתאימות, וממוצע ביניהן אינו דבר נכון. באופן כללי, במדידות שאמורות לתת את אותו המספר, אז הממוצע הנכון צריך להיות קרוב יותר למדידה בעלת השגיאה הקטנה יותר, כי יש עליה ודאות יותר טובה מכיוון שהשגיאה קטנה יותר, ולא סתם ממוצע חשבוני (זהו ממוצע משוקלל). השגיאה על הממוצע צריכה להיות קטנה מכל אחת מהשגיאות בנפרד. ‏Setreset • שיחה 00:01, 27 בנובמבר 2012 (IST)

רציתי את הנוסחה של זה (אמרו לי שממוצע השגיאות מתאים, אבל האומר הוא סטודנט כמוני). אם אתם רוצים נתונים אמתיים: מדדתי אנתלפיית סובלימציה של ארגון ב2 ניסויים דומים. באחד קיבלתי $7988\pm 642$ בשני קבלתי $8287\pm 987$. ואני מתבקש לפי התדריך להתייחס לממוצע המדידות. אז איך אני מוצא את השגיאה בממוצע? 109.64.206.238 14:50, 27 בנובמבר 2012 (IST)

האם ידוע לך למה הכוונה בניסוח "$7988\pm 642$"? עוזי ו. - שיחה 16:07, 27 בנובמבר 2012 (IST)

זה אומר שהערך "האמתי" שמדדתי הוא משהו מספר בין 7988+642 לבין 7988-642, אבל המכשיר (והניסוי) לא מאפשר מדידה מדויקת יותר. לא כך זה בכל ניסוי? 109.64.234.171 22:32, 27 בנובמבר 2012 (IST)

בדרך כלל הפירוש של שגיאה פלוס מינוס הוא סטיית תקן. בדרך כלל גם לא מתכוונים שכל מספר בטווח הפלוס מינוס יצא בסיכוי שווה, אלא יש התפלגות נורמלית, שבה הסיכוי של המדידה שלך להיות במרחק X מהערך ה"אמיתי" קטן עם המרחק אבל לא מתאפס, כלומר המדידה לא תהיה רק בין שני הטווחים שציינת אלא גם מעבר להם, בסיכוי לא זניח.

לעניין עצמו: מוזר שבניסוי שהוא "דומה" כפי שאמרת, יוצאות שגיאות שונות. אני מנחש שמדובר בניסויים שונים. בהנחה שהמדידה נורמלית וכו', ואנחנו מנסים לקלוע לדעת המרצה, הייתי אומר שהממוצע צריך להיות ממוצע משוקלל עם משקלים של אחד חלקי השגיאה בריבוע, והשגיאה היא שורש של אחד חלקי סכום המשקלים. יש לנוסחאות הללו סיבה טובה כאשר ההתפלגות של השגיאה היא נורמלית. ‏Setreset • שיחה 23:12, 27 בנובמבר 2012 (IST)

הרחבת את אופקי בנושא שגיאות: לא חשבתי שזה גאוסיאן. אני נורא מתבלבל לראות נוסחה כתובה במילים, אתה יכול לכתוב אותה מתמטית? השגיאות התקבלו טכנית מפלט רגרסיה של אקסל (שיפוע הגרפים מוצג עם שגיאה). הניסויים ששיתי היו דומים כי מדדתי את אותו הגדול, אבל פעם על ידי מקר לחם ופעם מחם לקר. אז קיבלתי 2 ישרים (לוג לחץ כפונקציה השל 1 חלקי טמפרטורה) קרובים, אבל עם שיפוע טיפה שונה ופלט הרגרסיה מראה שיש גם שגיאה שונה בשיפוע. 109.64.234.171 23:26, 27 בנובמבר 2012 (IST)

אין לי כרגע פנאי להרחיב, אבל אם אתה רוצה לעשות את זה כמו שצריך אתה חייב לרשום פונקציה. זאת אומרת, אתה צריך לרשום את הגודל המבוקש כפונקציה של הגדלים המדידים, ולחלץ את השגיאה בעזרת נגזרות חלקיות. לי לא ברור מהם הגדלים המדידים ומהו הגודל המבוקש, אבל לך זה צריך להיות מאוד ברור. באופן אישי לא הייתי סומך על השגיאה שמספק אקסל, במיוחד מכיוון שלמיטב ידיעתי אקסל בכלל לא לוקח בחשבון את שגיאות המדידה. משה פרידמן - שיחה 08:19, 28 בנובמבר 2012 (IST)

אני מנחש שמדובר במשוואת קלאוזיוס-קלפרון. השגיאה שקיבלת (מאקסל?) היא שגיאה אקראית, ולא השגיאה הכוללת, שיש בה את השגיאה השיטתית. לשגיאה האקראית הרגרסיה של אקסל פלוס הנוסחה שכתבתי למעלה במלים מספיק נכונה. את השגיאה השיטתית הרבה יותר קשה להעריך. קרא את הערך שגיאת מדידה לכשייכתב (אכתוב אותו בשבועות הקרובים אז תמשיך לעקוב). בינתיים יש חומר בערך כיול ובערך דיוק ונכונות. ‏Setreset • שיחה 20:30, 28 בנובמבר 2012 (IST)

קירוב זומרפלד

במצב מוצק, למה מותר לעשות את המעבר הבא $\int _{0}^{\infty }g(\epsilon )f(\epsilon ,\mu )d\epsilon =\int _{0}^{\mu }g(\epsilon )d\epsilon +{\frac {\pi ^{2}}{6}}g'(\mu )(K_{b}T)^{2}$ ? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

תרשים של פיצוץ גרעיני או של תגובה כימית?

אמש נפתחו מהדורות החדשות עם ידיעה מרעישה על תרשים מחשב שנוצר במסגרת תכנית הגרעין האיראנית. אין לי ספק שהם מפתחים נשק גרעיני ושהכוונות שלהם רעות, אבל התרשים לא נראה לי משכנע. היחידות בצד ימין אינן kt TNT (קילוטון TNT) כי אם kT, שזו מכפלת קבוע בולצמן בטמפרטורה. המהדרין יסמנו k_BT, אבל לא כולם שולטים ב-LaTeX והשמטת ה-B שכיחה למדי. מה דעתכם, האם מדובר בתרשים של תגובה כימית, חישוב תרמו-דינמי או אשכרה פיצוץ גרעיני? ואיך עוד לא שמענו את הבלוגרים מגחכים על ההדלפה המרעישה הזו? ליאור पॣ • י"ד בכסלו ה'תשע"ג • 13:39, 28 בנובמבר 2012 (IST)

זה אכן מגוחך להסיק על סמך גרף כזה משהו. יחד עם זאת, היחידות בצד שמאל הינן יחידות של הספק, שזה מתאים לתיאור פיצוץ. אני מניח שפירוש היחידות בצד ימין זה אכן משהו שקשור לאנרגיה. אני לא מניח שמדובר בקילוטון לשניה, כי אם כן עוצמת הפיצוץ המתוארת בגרף היא בערך אלפיים מגהטון, בערך פי 40 מהפצצה העוצמתית ביותר שנוסתה אי פעם. משה פרידמן - שיחה 14:24, 28 בנובמבר 2012 (IST)

הכתבה חוזרת על טעות שגרתית, כשהיא מכנה את הגרף "עקומת פעמון". אולי צורת העקומה דומה לזו של ההתפלגות הנורמלית (הקרויה בשם זה), אבל ההתפלגות הנורמלית מתארת פיזור במרחב, ולא התפתחות של תהליך לאורך זמן. עוזי ו. - שיחה 00:24, 29 בנובמבר 2012 (IST)

סכום של סדרה

לסדרה האינסופית הבאה יש תוצאה: $\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}={\frac {\pi ^{2}}{6}}$

האם קיימת נוסחה ל: $\sum _{k=1}^{N}{k^{2}}$ -יונה בנדלאק - שיחה 16:59, 28 בנובמבר 2012 (IST)

$\sum _{k=1}^{N}{k^{2}}={\frac {N(N+1)(2N+1)}{6}}$ ‏ Easy n - שיחה 16:55, 28 בנובמבר 2012 (IST)

האם יש גם נוסחה ל $\sum _{k=1}^{N}{k^{3}}$ וכלל כלשהוא למצוא סכום של טור בחזקה כלשהיא? -יונה בנדלאק - שיחה 16:59, 28 בנובמבר 2012 (IST)

$\sum _{k=1}^{N}{k^{3}}=\left(\sum _{k=1}^{N}k\right)^{2}$. אני לא מכיר נוסחה כללית. Easy n - שיחה 17:11, 28 בנובמבר 2012 (IST)

ראה משפט ניקומאכוס למקרה המעוקב ומספר ברנולי למקרה הכללי. דניאל • תרמו ערך 19:49, 28 בנובמבר 2012 (IST)

התנגדות של האוויר

איני יודע איך לגשת בדיוק לשאלה הבאה. ניסיתי לפצל את וקטורי המהירות, אבל הזווית משתנה כל הזמן ויש שינוי במהירות גם בציר X, שאני לא בדיוק יודע איך להביע אותו. אנא עזרו לי: מסה נקודתית m נזרקת אופקית במהירות V_0 מקצה מגדל שגובהו h. במהלך תנועתה פועלת על המסה התנגדות האוויר הגורמת לחיכוך של ${\overrightarrow {f}}=\beta {\overrightarrow {v}}$. מצאו את מיקום המסה כפונקציה של הזמן. אביעד‏ • שיחה 20:17, 28 בנובמבר 2012 (IST)

תתחיל מלכתוב את משוואות התנועה בצירים X ,Y. ‏Setreset • שיחה 23:31, 28 בנובמבר 2012 (IST)

התחל בחוק השני של ניוטון, פעמיים: לציר x ולציר y. בציר x התנועה כמובן, אינה קצובה, בשל התנגדות האויר. אל תיטרד מהזווית, משום שבסופו של דבר, תקבל שני שיעורים עבור המיקום המבוקש. שים לב גם לכך שאגף הכוחות בציר y כולל שני כוחות מנוגדים. אם תכתוב נכון את שתי המשוואות, תקבל שתי משוואות דיפרנציאליות מסדר ראשון, שמפתרונן תקבל את משוואות התנועה של המהירויות בשני הצירים. לאחר קבלת משוואות אלה, תוכל לקבל מהן, באמצעות אינטגרציה, את הביטויים עבור ההעתקים בשני הצירים, ומידיעת שיעורי המיקום ההתחלתי (x₀=0,y₀=h), תקבל, לבסוף, את הפונקציות הנותנות את שיעורי המיקום הסופי כפונקציה של הזמן. בהצלחה, בנצי - שיחה 05:00, 29 בנובמבר 2012 (IST)

תודה. לאחר שהבעתי את התאוצות מצאתי בעזרת קינמטיקה את המשוואות הבאות: $2mx=v_{0}t-\beta vt^{2}\sin \alpha$, ו-$2my=(mg-\beta v\cos \alpha )t^{2}$. אני לא בטוח שכלל המשוואות האלה נכונות, וגם אם כן, נראה לי בעיה לפתור אותן. אביעד‏ • שיחה 18:13, 29 בנובמבר 2012 (IST)

המשוואות לא נכונות. לא צריך להיות זמן במשוואות. אתה השתמשת בפתרון של תנועה בליסטית ללא חיכוך וניסית להכניס את החיכוך. המשוואות הן החוק השני של ניוטון: מסה כפול תאוצה שווה לסכום הכוחות. נסה לכתוב בנפרד כל אחד מהכוחות, אחר כך את כל אחד מהכוחות בכל ציר בנפרד, ואז זה צריך להיות ברור איך לכתוב את המשוואות. אחר כך אפשר לטפל בפתרון שלהן. ‏Setreset • שיחה 21:20, 29 בנובמבר 2012 (IST)

שאלה בחוקי קפלר

לוויין נע במסלול מעגלי סביב כדור הארץ ברדיוס R ידוע. איך מוצאים את המהירות שלו? אני יודע שהתוצאה היא $v={\sqrt {GM/R}}$ אבל לא מבין איך זה יוצא ככה(לפי מה יודעים)? 109.64.197.85 22:56, 28 בנובמבר 2012 (IST)

משווים את כוח המשיכה במרחק כזה למסה כפול התאוצה הצנטריפטלית שיש לתנועה סיבובית ברדיוס כזה (כפונקציה של המהירות). eman • שיחה • ♥ 23:05, 28 בנובמבר 2012 (IST)

תוצאה זו מתקבלת כמעט מיידית, מהביטוי לחוק השני: כאשר הביטוי לכוח הוא כוח הכבידה, ואילו הביטוי לתאוצה הוא התאוצה הרדיאלית. כשהביטויים הללו נכתבים בצורה מפורשת ומבצעים את הצמצום הדרוש מקבלים את המבוקש, אחרי הוצאת שורש ריבועי. בנצי - שיחה 00:37, 29 בנובמבר 2012 (IST)

כל הקוונטים האלא זה שטויות

יש איזה סטודנט לפיזיקה (גם אני אחד משם) שכל הזמן בשיחה איתי מדבר על זה שכל תורת הקוונטים היא שקר כי הפילוסופיה של מי שפתח היא שטויות פוזיטביסטוית. נעזוב בצד את האגו של סטודנט סמסטר 4 שחושב שהוא חכם מכל הפיזיקאים גם יחד, אלא נתמקד בעיקר:

הוא אומר שהפילוסופיה (השגויה והמופרכת) היא שרק מה שאנחנו מודדים קיים ולכן האקט של המדידה יוצר את המציאות. וזה לא יתכן כי למציאות יש קיום. ולכן הפילוסופיה מאחורי מכניקת הקוונטים שגויה ולכן כל התורה היא פרשנות לא נכונה של הניסוי. לדוגמה : אם החלקיק קורס למצב P1 מסוים ברגע המדידה אז לפני כן אומרים שהוא בסופרפוזיציה של נגיד P1 וP2 ולכן אין לו תנע מוגדר כלומר לפני המדידה לא היה לו תנע בכלל אלא המדידה יצרה אותו. שלדעת אותו הבחור אומר רק שהיו פרמטרים שאנחנו לא יודעים שגרמו לתנע להיות דווקא P1.

אני טענתי שתאוריות משתנים חבויים הופרכה הוא אמר שהיא לא יכולה להיות מפרכת היא אז העולם לא יהי קיים ולכן כל הוכחה שאין משתנים חבויים היא בעלת סתירה. 109.65.189.93 10:51, 29 בנובמבר 2012 (IST)

אם החבר שלך מראש מנמק את דבריו בקביעות לא מסוברות של מה יכול להיות ומה לא (ובהנחה שאינו אלוהים) אין לך מה לדון איתו. תאוריות משתנים חבויים לא הופרכה. משפט בל קובע שאם היא נכונה זה אומר לוותר על עקרונות אחרים שהיית מצפה שייתקיימו בעולם. וגם ללא שום תלות בפרשנות של מכניקת הקוונטים הטענה ש"תורת הקוונטים היא שקר" היא אמירה אומללה. התורה הפיזיקלית עצמה (ללא פרשנות) היא התורה המדויקת ביותר שפותחה מאז ומעולם שחוזה ברמת דיוק מדהימה את תוצאות הניסויים. דניאל • תרמו ערך 11:37, 29 בנובמבר 2012 (IST)

אמרתי משהו בערך דומה. הוא אומר שהמודל המתמטי נבנה ככה שיחזה טוב את התוצאות, אבל זה לא אומר שהתורה נכונה. גם המודל הניוטוני חוזה טוב תוצאות מסוימות, אבל יש בו הנחות פילוסופיות לא נכונות. לבחור הזה יש הגיון ברמה שאני לא אגיע אליה, והוא חושב שעם ההיגיון הזה הוא מסוגל להבין את היקום(שזו לדעתי טעות. פיזיקה היא לא הגיון טהור כמו מתמטיקה אלא מדע ניסיוני) ושהיקום מחויב לחיות לפי חוקי ההיגיון. אבל שוב, נעזוב אגו בצד. הטענה המרכזית היא שהעולם קיים גם מחוץ למדידה ואם לא ראינו את הצד האפל של הירח לא אומר שאין לו צד אפל. ולעומת זאת הפילוסופיה של המדידה הקוונטית אומרת שעצם המדידה יוצרת את התוצאה. כלומר המודד בורא את המציאות. 79.177.189.122 11:48, 29 בנובמבר 2012 (IST)

הטענה שהעולם קיים גם מחוץ למדידה (בהתעלם כרגע מהשאלה מהי מדידה) היא טענה שאינה נתמכת על ידי שום ניסוי (ולא ברור לי אם היא יכולה בכלל). אם החבר שלך מאמין בהנחה הזו מסיבות פילוסופיות, זה בסדר. יש פיזיקאים רבים ומכובדים שחושבים כך. זו לא פיזיקה, זו מטאפיזיקה. דניאל • תרמו ערך 11:57, 29 בנובמבר 2012 (IST)

חוקי קפלר

אמרנו חתכי חרוט. יש חתך שהוא עובד ישירות דרך הקדקוד (וניצב למישור הבסיס) חתך זה הוא "משולש" (לא סגור). האם יתכן מסלול שהוא מורכב מ2 קטעים ישרים?

בנוסף, יש את המסלול הכי פשוט- חלקיק נופל על מסה ללא שום התנגדות( מהירות לכיוון ניצב) כלומר מסלול לינארי. הוא לא חתך חרוט, נכון? 109.65.219.92 11:27, 29 בנובמבר 2012 (IST)

אני דווקא כן הייתי אומר שהמסלול של חלקיק שנופל בקו ישר, נובע מאחד מחלקי המשולש הזה. זה כמו שבהיפרבולה המסלול הוא רק אחד הענפים שלה. eman • שיחה • ♥ 11:35, 29 בנובמבר 2012 (IST)

קוונטים

האם הטענה הזאת אומרת לכם משהו: "ממוצע של קואורדינטה בריבוע, על פני פונק' הגל של מצב היסוד הינה רדיוס בוהר בריבוע". בהקשר של מולקולת מימן (H2) מישהו יודע איך להוכיח את זה? 79.177.189.122 23:04, 29 בנובמבר 2012 (IST)

יש את זה בכל ספר-לימוד בסיסי העוסק בפיזיקת קוונטים. בנצי - שיחה 09:48, 30 בנובמבר 2012 (IST)

אין את זה בCohen Tanugi ולא בלנדאו-ליפשיץ (בדקתי). 109.65.204.252 09:44, 1 בדצמבר 2012 (IST)

כבר עשיתי קורס אחד בקוונטים. אני לא מבין את הנוסח של מה שכתוב. מה זה "ממוצע על פני פונק' גל". למה קשור רדיוס בוהר? 79.177.189.122 10:14, 30 בנובמבר 2012 (IST)

אם אני זוכר נכון, זאת פשוט ההגדרה של רדיוס בוהר. רדיוס בור הוא הרדיוס הממוצע של מצב היסוד של אטום המימן, ומחשבים אותו כפי שנכתב למעלה. ‏Setreset • שיחה 13:48, 30 בנובמבר 2012 (IST)

אתה יכול להראות איך עושים את זה? לא ברור לי מה זה ממוצע על קואורדינטה בריבוע על פני פונקציית גל(הנוסח לא מובן). 109.67.244.135 16:00, 30 בנובמבר 2012 (IST)

הכונה לאינטגרל שבתוכו מוכפלים: R כפול פונקציית הגל (כפונקציה של R תטה ופי) כפול הצמוד של פונקצית הגל כפול dR כפול היעקוביאן (R2 כפול סינוס תטא). ‏Setreset • שיחה 16:59, 30 בנובמבר 2012 (IST)

אתם מתייחסים לזה כאילו שזה מובן מאיליו. זה לא (אחרת לא הייתי שואל). ניסיתי לכתוב את מה שסטריסט כתב במילים, אבל כל מה שהצלחתי זה: $\left\langle \psi |{{x}^{2}}|\psi \right\rangle =\int {r}\psi (r,\theta ){{\psi }^{*}}(r,\theta ){{r}^{2}}\sin \theta$ אני לא בטוח זאת הכוונה, אבל זה הפרשנות הכי הגיונית של המילים "ממוצע של קואורדינטה בריבוע, על פני פונק' הגל". עכשיו- איפה רדיוס בוהר? בבקשה, אל תתעלמו ותכתבו "זה כל טיפש יודע לעשות". בחיים לא דיברו איתנו על מהמושג רדיוס בוהר בקורס קוונטים והזה שאלה בקורס של כימיה(!) שהם לא יודעים מה כן למדנו ומה לא. 109.65.204.252 09:16, 1 בדצמבר 2012 (IST)

מצוין, זאת הכוונה. הטענה כותבת קואורדינטה בריבוע, אז תכניס את R בריבוע במקום R שכתבתי קודם. את פונקצית הגל המפורשת תמצא בערך באנגלית: hydrogen atom, רדיוס בוהר מתחבא בתוכה. הצב בנוסחה, שים לב שיש שם רו במקום R וכתוב מה הקשר ביניהם. פתור את האינטגרל ותקבל משהו דומה לטענה. לי יצא עם פקטור 3 ואני לא ממש יודע מה לעשות איתו, אולי טעיתי בדרך. אולי הטענה לא מדויקת. ‏Setreset • שיחה 13:18, 1 בדצמבר 2012 (IST)

יוצא לי גם מוזר, עם הרבה גורמים לא צפויים. פונקציית הגל היסודית היא${{\psi }_{n\ell m}}(r,\vartheta ,\varphi )={\sqrt {{\frac {1}{\pi }}{{\left({\frac {1}{{a}_{0}}}\right)}^{3}}}}{{e}^{-r/{{a}_{0}}}}$. אז$\int _{0}^{+\infty }{{r}^{4}}dr\int _{0}^{\pi }{\sin }\vartheta d\vartheta {\frac {1}{\pi }}{{\left({\frac {1}{{a}_{0}}}\right)}^{3}}{{e}^{-2r/{{a}_{0}}}}={\frac {2}{\pi }}{{\left({\frac {1}{{a}_{0}}}\right)}^{3}}{\frac {3{{a}_{0}}^{5}}{4}}={\frac {3{{a}_{0}}^{2}}{2\pi }}$. מאיפה הפקטורים המיותרים?

שכחת אינטגרל על פי שיוצא 2*פאי, ואז יוצא לך בדיוק כמו לי. חיפשתי עכשיו באינטרנט, המקור הזה: [4] עושה בדיוק את אותו תרגיל, ואם תסתכל על כל האופציות אז ברור למה הכוונה. אינטגרל כמו שעשינו יצא נכון, הכוונה היא למצוא את הממוצע רק של אחת הקואו' בריבוע, למשל X^2. ברור גם למה יוצא שהאינ' של R^2 יוצא פי שלוש (שכחת בשוויות הראשון למעלה, ממוצע של X^2 הוא שליש הממוצע של R^2). אני לא חושב שיש משהו עמוק מאחורי השימוש דווקא באחת הקואורדינטות. ‏Setreset • שיחה 21:02, 1 בדצמבר 2012 (IST)

מכפלה טנזוריאלית בקוונטים

אתם יכולים להסביר את המשמעות של הטענה: "מרחב הילברט כולל של חלקיק קוונטי הוא מכפלה טנזוריאלית בין שני מרחבים $E_{orb}\times E_{spin}$ (במחברת זה עם עיגול על הX)".

1. מה המשמעות המתמטית של זה?
2. מה משמעות הפיזיקלית של זה? ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

זהות מרוכבת

למה יוצא ש$ab^{*}e^{-ix}+a^{*}be^{ix}=2Re(a^{*}be^{ix})$? איך מפתחים את זה (או איך זוכרים)?109.67.244.135 17:09, 30 בנובמבר 2012 (IST)

זה סתם מקרה פרטי של הזהות (מספר מרוכב ועוד הצמוד שלו) = (פעמיים החלק הממשי של המספר). ‏Setreset • שיחה 17:17, 30 בנובמבר 2012 (IST)

מודל דרודה

השאלה שלי נמצאת כאן. אני לא ממש הבנתי איך לפי הנתונים ניתן למצוא את זמן הרלקסציה (זמן בין ההתנגשויות) ולא איך מוצאים את ריכוז האלקטרונים. 79.181.219.23 18:07, 30 בנובמבר 2012 (IST)

א. באיזה קורס או מסגרת אתה לומד ? מאיזה ספר-לימוד לקוחה השאלה ?

ב. עפ"י נתוני הטבלה, יש למצוא קודם את צפיפות האלקטרונים, אותה מוצאים משיקולים בסיסיים לפי $n=6.022\times 10^{23}{\frac {Z\rho }{A}}$, כאשר A הוא המספר האטומי, Z הוא מספר האלקטרונים שתורם כל אטום, ו-$\rho$ הוא המסה הסגולית של המתכת. הערך $6.022\times 10^{23}$ הוא מספר אבוגדרו, כלומר, מספר האטומים למול.

ג. את הזמן בין ההתנגשויות (זמן הרלקסציה, $\tau$) ניתן למצוא בשתי דרכים: 1. עפ"י היחס בין המהלך החופשי הממוצע לבין המהירות הממוצעת. פתרון זה לא מעשי במקרה שלך, בהעדר נתונים. 2. עפ"י הביטוי למוליכות הסגולית, לאחר שכבר חישבת את צפיפות האלקטרונים. בהצלחה, בנצי - שיחה 21:31, 30 בנובמבר 2012 (IST)

א. קורס מצב מוצק, תואר ראשון. זה לא מספר לימוד (אם כן, לא יודע לי מאיזה) אלא שאלה שפורסמה על ידי צוות הקורס

ב. מסה סגולית? האם יש דרך להשתמש בנתונים שיש לי? יש צפיפות אטומים לנפח. אחרי שיש לי את ריכוז האלקטרונים זה כבר שאלה פתורה. אז השאלה היא רק איך משתמשים בנוסחה שנתת. מה זה "מספר האלקטרונים שתורם כל אטום"? איך יודעים? איך במקום רו, אבוגדרו וA משתמשים בכמות אטומים לנפח?

ותודה. 79.181.219.23 22:17, 30 בנובמבר 2012 (IST)

מצב מוצק, שאלה

שאלה כאן.

בסעיף א' אני חושב שזה טמפרטורה כפול קבוע בולצמן. בסעיף ב' אני לא יודע. מה זה צפיפות זרם האנרגיה? איך מוצאים? 79.181.219.23 20:32, 30 בנובמבר 2012 (IST)

חור שחור, ניסוי מחשבתי

חללית נקודתית עם צופה שיושב עליה החליטה לחקור חור שחור. היא חוצה את רדיוס שוורצשילד בנפילה חופשית ומפעליה מנועים מיד עם כניסתה בשביל להאט את הנפילה. ואז היא שלוחת קרן לייזר למראה התלויה מהצד השני של אופק אירועים. האם הצופה יראה את ההשתקפות של קרן?

מהירות האור היא C בכל מערכת שהיא גם ביחסות הכללית! ולכן הוא אמור להצליח. אם כך, בעולם של הצופה שנפל לחור השחור, הוא יכול גם לשלוח מסר לכדור הארץ "הכל טוב ויפה כאן, באו לבקר" ובמערכת שלו הוא גם יראה את תושבי כדור הארץ באים( נו הבנתם את הרעיון- יש צופה נוסף מחוץ לאופק אירועים שמתקשר עם הצופה שנפל)? 79.183.232.248 16:27, 1 בדצמבר 2012 (IST)

ביחס לצופה שנמצא בחוץ, לוקח לחללית זמן אינסופי לעבור את אופק האירועים, ולכן הניסוי הזה לא יצליח. ‏Setreset • שיחה 20:52, 1 בדצמבר 2012 (IST)

זה כל הקטע: אני מדבר על הצופה שנמצא בפנים! הוא יוכל להמשיך את הניסוי ולשלוח מסרים לצופה בחוץ ואמור לצפות ממנו לתגובה. 79.180.248.89 21:46, 1 בדצמבר 2012 (IST)

לצופה שנמצא בפנים ייקח גם כן זמן אינסופי לעבור את אופק האירועים, ביחס לצופה שנמצא בחוץ. ‏Setreset • שיחה 22:40, 1 בדצמבר 2012 (IST)

אתה טועה. צופה שנופל לתוך חור שחור לא ירא את החור הולך ומתקרב אליו עד אינסוף, אלא אפילו לא ישים לב שהוא עבר את אופק האירועים (בדוק זאת!). 79.180.195.60 23:26, 1 בדצמבר 2012 (IST)

המשפט האחרון שלך נכון לגבי חור שחור על-מסיבי, ולא נכון לגבי חור שחור כוכבי. בכל מקרה אין קשר בין המשפט הזה למה שאני כתבתי, מבחינה לוגית. בהצלחה. ‏Setreset • שיחה 09:39, 2 בדצמבר 2012 (IST)

קרינת גוף שחור, איך זה שיש כוכבים?

איך זה שכוכבים מרוחקים יחסית כמו פלוטו (כוכב לכת ננסי) לא "מקרינים את עצמם למוות"? כמות הקרינה שמקבל עצם כזה מהמשמש קטן בהרבה מקרינת גוף שחור שהוא אמור לפלוט. איך זה מסתדר? 79.177.248.171 17:52, 1 בדצמבר 2012 (IST)

עוצמה של קרינת גוף שחור יחסית לטמפרטורה ברביעית. הגוף קורן ומתקרר עד שהוא מגיע לשווי משקל, כלומר הקרינה שהוא פולט שווה לקרינה שהוא מקבל. הטמפ' בחלל החיצון הרחוק היא 2.3 מעלות קלווין, שהיא הטמפ' של קרינת הרקע הקוסמית, שהיא הטמפ' של גוף שאינו מקבל כלל קרינה ממקור נוסף. לפי הערך, הטמפ' של פלוטו היא בין 33-55 קלווין, ואפשר לבדוק את זה מול הקרינה שהוא מקבל מהשמש. באופן כללי גופים גם מחממים את עצמם מבפנים בתגובות גרעיניות, וזאת יכולה להיות הסיבה לסטיה, אם קיימת, מהחוקים הנ"ל. ‏Setreset • שיחה 20:51, 1 בדצמבר 2012 (IST)

כלל הזהב של פרמי, פיתוח

כאן מופיע הפיתוח של מקרה של חלקיק בקופסה( מקור: הרצאות בטכניון). הצבע הכתום זה מה שלא הבנתי. בהרצאה הוזכרה המילה יעקוביאן נראה לי בהקשר של זה. אבל לא מובן לי מה הקשר, במיוחד מה זה הפאי הזה. 79.180.195.60 22:03, 1 בדצמבר 2012 (IST)

מעכבי הצמתת טסיות > פירוש עברי

― הועבר לדף ויקיפדיה:הכה את המומחה

שאלה פילוסופית בקוונטים

למה אי אפשר להישאר במודל הישן ולא לקבל את המונח של קריסת פונקציית גל?

ניקח את הדוגמה של ספין חצי. אני אומר שכל אלקטרון משתחרר מאטום עם ספין אחד ויחיד שנקבע על ידי השחרור שלו (כלמור כל התנאים במכשיר שפולט את האלקטרון). והגלאי (לדוגמה שטרן גרלך) רק מאתר את הספין שכבר היה מראש. ככה שלא המדידה קובעת את התוצאה, אלא התוצאה נקבעה מראש ויש דטרמיניזם מחולט (גלאי בסך הכל עוזר לנו לדעת באיזה ספין האלקטרון נפלט). מכאן שאחרי שגילינו שלחלקיק יש ספין פלוס חצי, אז מן הסתם בכל המדידות זה יהיה אותו דבר(כי שום דבר לא שינה את הספין שלו). מה סותר את המודל שלי? 79.176.209.114 15:22, 2 בדצמבר 2012 (IST)

הרבה דברים, אבל נתחיל עם העובדה שלכל כיוון (של הספין) שתכוון את הגלאי תקבל שתי אפשרויות נפרדות (למעלה או למטה). מעבר לזה יש את העובדה שאפשר לסובב את הספין ולקבל סתירה די מהירה. כמובן שמודל יותר מסובך דורש ניסוי יותר מורכב והסתירה הסופית למודלים מהסוג הזה היא הפרת אי שיוויון בל ירון ק. - שיחה 13:48, 21 בדצמבר 2012 (IST)

האם יש אפקטים קוונטיים במוחו של אדם?

האם ישנם אפקטים אקראיים שהתוצאה שלהם לא נקבעה מראש בתוך מוחו של יצור חי? כשאני מדבר על אקראיות אני לא מתכוון לזריקת מטבע( שלצורך העניין זה לדטרמיניזם מוחלט) אלא לאקריות במובן קוונטי. 79.176.209.114 15:24, 2 בדצמבר 2012 (IST)

רוג'ר פנרוז טוען שכן (ושהם עומדים מאחורי הבעיה הפסיכופיזית), אבל אני לא חושב שיש לזה הוכחות כלשהן. 109.160.166.43 18:22, 2 בדצמבר 2012 (IST)

כמובן שיש אפקטים קוונטיים. השאלה האם אפקטים קוונטים במוח הם בעלי השפעה על תהליכים מקרוסקופיים (כגון קבלת החלטות). למיטב ידיעתי אין תשובה לשאלה הזו. פרופ' חיים סומפולינסקי סבור שהתשובה לשאלה שלילית. לגבי הבעיה הפסיכופיזית, לא ברור האם זה עוזר, משום שגם אם יש השפעה לתהליכים כאלו הרי שהם חייבים להיות אקראיים לחלוטין. משה פרידמן - שיחה 18:51, 2 בדצמבר 2012 (IST)

יש תשובה לגבי הראשונה, וישנם מחקרים העוסקים בכך, ע"י קבוצות שונות, אם כי אלה עדיין בחיתוליהם. קבלת החלטות, כמו זכירה, למידה, מודעות ועוד, הן תופעות הנובעות ממורכבותה של מערכת הנוירונים המעורבים בכך (ראה כאן, וגם כאן), ובעיקר, מורכבות הקשרים ביניהם. שתיים מהבעיות הגדולות ביותר הן הקושי לנסח פורמליזם מתימטי מתאים לתיאור הבעיה, והקושי למדל מערכת כזו. מדע המורכבות, כאמור, עדיין בתחילתו, אבל אפקטים בסיסיים שלו כבר מוכרים. בנצי - שיחה 14:54, 3 בדצמבר 2012 (IST)

שטח סגולי

בהקשר של כימיה, ספיחה כימית. מה זה "שטח סגולי של סיליקה" (מה זה שטח סגולי בכלל ושל סיליקה בפרט). 79.183.213.232 16:38, 2 בדצמבר 2012 (IST)

ראו שטח פנים סגולי. ‏Setreset • שיחה 20:55, 2 בדצמבר 2012 (IST)

מה שנקרא הכחלה (בסיסית) בזמן אמיתי. עמדתי להעיר לך על הקישור האדום, אבל טוב שהתעכבתי בשל שיחת טל' חשובה. ראו גם דוגמא לשטח פנים סגולי. בנצי - שיחה 22:35, 2 בדצמבר 2012 (IST)

כימיה, יחידות

הסתבכתי עם יחידות מדידה בכימיה. התרגיל כאן. הפיתרון שלי זה כל מה שממולא בטבלה והצבה לנוסחה (נתנו לנו נוסחה ואני רשמתי את המספרים). אני לא מסתדר עם היחידות. האם אפשר להפוך את זה למשהו יותר סימפטי? אם למישהו יש נתונים שחסרים בטלבה, תודה! 79.183.213.232 17:20, 2 בדצמבר 2012 (IST)

א. עליך לדאוג שהיחידות תהיינה תואמות. אם היבנתי נכון את שאלתך, מה ש'מדאיג' אותך הם שניים: d (המסה הסגולית) ו-M הנתונה ביחידות amu (או דלטון). יחידות נכונות של d הם gr/cm³ ולא כפי שרשמת בטבלה. 1 דלטון (או amu) שווה ל-$1.66\times 10^{-24}$ גר'. ערכים אלה שייכים ליחידות תואמות. בדוק שכך עשית.

ב. נכון לכתוב פאזה נוזלית או מופע נוזלי, ולא אחרת. כך גם עם "ערכים ספרותיים", שלו משמעות אחרת ממה שהתכוונת. מקובל לקרוא לזה 'ערכים מהספרות'. בהצלחה, בנצי - שיחה 19:54, 2 בדצמבר 2012 (IST)

כימאים, לך תבין אותם. לא אני כתבתי את הטבלה, אני רק כתבתי את הערכים במקומות הנכונים. וגם לי נראה מוזר שהם נתנו לי נוסחה שיש בתוכה אי התאמה של יחידות (נתנו נוסחה ואני רק הצבתי לתוכה את הנתונים שמצאתי באנגלית). 79.176.225.66 20:30, 2 בדצמבר 2012 (IST)

למה אסטרונאוט מרחף?

למה אסטרונאוט בחללית נעה במסלול סביב כדור הארץ מרחף? סכום הכוחות עליו הוא אפס? למה? למה אסטרונאוט במעלית נופלת מרחף? הסבר ברמת תיכון ותודה מראש. 79.181.213.154 18:52, 2 בדצמבר 2012 (IST)

א. שקול הכוחות הפועלים עליו או על החללית לא יכול להיות שווה ל-0, משום ששניהם מקיפים את כדוה"א במסלול, נניח מעגלי, לשם פשטות. אני גם מניח שאתה זוכר מלימודים קודמים, שלפי החוק הראשון של ניוטון, שקול הכוחות הפועלים על גוף שווה ל-0 רק אם הוא נע במהירות שגודלה קבוע בקו ישר (כיוון קבוע). זה לא המקרה שלך. אם תרשום נכון את הביטוי לחוק השני של ניוטון, תיווכח כי תאוצת הנפילה שלו ושל המעלית גם יחד, היא בדיוק התאוצה הרדיאלית שלו (ברר קודם לעצמך איך מוגדרת תאוצת נפילה - זה יעזור לך לקבל את המסקנה).

ב. ריחוף מוגדר כמצב בו שקול הכוחות הפועלים על גוף שווה ל-0. גוף הנמצא במעלית אינו מרחף, מלבד בתנאים ספציפיים המהווים מקרה פרטי: כאשר המעלית, וכל אשר בה, מאיצה כלפי מטה בתאוצה השווה ל-g. כתוב לעצמך את המשוואה המפורטת עבור החוק השני, והדבר יתברר לך די מייד. בנצי - שיחה 19:15, 2 בדצמבר 2012 (IST)

אני חושב שבמקרה ב' ישנו כוח אחד- גרוויטציה שפועל על האדם בתוך החללית וההסבר לתופעת הריחוף הוא שגם המעלית מאיצה באותה התאוצה וזה יוצר מצב שהאדם לא מרגיש את הנורמל מהרצפה. המקרה הראשון יותר מסובך- אדם בתוך החללית בכל אופן לא מרגיש כוח, אחרת היה נמשך לאחד הקירות. הוא בעצמו לא יודע שהוא נמצא בחללית, אלא פועל אליו כוח אחד, גרוויטציה. אז הגיוני שהוא יפול יחד עם החללית כמו מעלית נופלת. אבל עובדה שבגלל שהחללית מסתובבת אז היא לא נופלת (כנראה תאוצה רדיאלית שווה לתאוצת הכובד). אז איך זה שהאסטרונאוט לא יכול לעמוד אלא מרחף? 79.181.213.154 19:36, 2 בדצמבר 2012 (IST)

אני משוכנע שלא ביצעת את בדיקת הביטויים כפי שהסברתי קודם. המשפט הראשון שלך נכון, אבל אתה מכריח את עצמך להסביר אינטואיטיבית במילים, במקום לברר לעצמך את ההוכחה המדוייקת לכך. אני רואה זאת גם מהביטוי שרשמת בסוגריים: "כנראה תאוצה רדיאלית שווה לתאוצת הכובד" - כדי להשתכנע בכך אתה חייב לרשום את הביטוי לחוק ה-2 בצורה מפורשת ומפורטת. לפני כן אין טעם לדבר או לדון. אין תחליף לעבודה יסודית. בנצי - שיחה 20:04, 2 בדצמבר 2012 (IST)

העיניין הוא שהתנועה המעגלית שנגרמת רק בגלל כוח הכובד, גם היא סוג של נפילה. החללית נופלת, אבל כל הזמן האדמה מתחתיה מתעקמת בעיגול, והיא אף פעם לא מפסיקה ליפול (בניגוד למקרה של המעלית). eman • שיחה • ♥ 23:47, 2 בדצמבר 2012 (IST)

לפי דבריו של קיפודנחש, בתאריך 25 בינואר 2011: "כיוון שאנו חיים על פני כדור (במלים אחרות הכבידה היא "נקודתית") נכנסים גורמים שגורמים להבדלים בין המקרים ("תוצא הגאות"). לסבר את האוזן: אם תשחרר שני כדורים במעלית הנופלת כך שיהיו במנוחה לגבי המעלית, בין מסלולי הנפילה שלהם יש זווית קטנה ולכן הם יתנהגו כאילו הם נמשכים זה לזה (מעבר למשיכה הכבידתית ביניהם). זה כמובן לא יקרה אם המעלית נמצאת בשדה כבידה אחיד - במקרה זה הזווית היא 0." קישור

אני מאוד אשמח אם מישהו יפרט בדיוק, מהם כל הכוחות הפועלים על גוף הנמצא במעלית שנופלת בנפילה חופשית, מהם הכוחות כל הפועלים על גוף הנמצא בלווין שנע סביב כדור הארץ, מהם הכוחות כל הפועלים על גוף הנמצא בתחנת חלל, וכן הלאה, כדי שההבדלים בין המצבים יהיו יותר ברורים. תודה. 80.230.25.130 05:24, 6 בדצמבר 2012 (IST)

מה ההבדל בין סרום לפלזמה?

― הועבר לדף ויקיפדיה:הכה את המומחה

שאלה טריקית (נראה לי) במכניקה

על קורה ארוכה ששיפועה a ומסתה M מונח ארגז שמסתו m הארגז קשור בחבל לגלגלת המעוגנת לקורה. הקורה מונחת על ריצפה אופקית חלקה. ברגע t=0 מתחיל המנוע לפעול ויוצר מתיחות בחוט הנתונה על ידי T=mgt/τ כאשר t קבוע ידוע. מקדם החיכוך הסטטי והקינטי בין הארגז לקורה המשופעת ידועים μs>μk, שניהם קטנים מ-1. המנוע פועל עד רגע t=3τ ואז נקרע החוט. א. מהי מהירות הקורה המשופעת כאשר הארגז הגיע לגובה המקסימלי? אביעד‏ • שיחה 00:21, 3 בדצמבר 2012 (IST)

צריך איור בשביל שיהיה מובן מה קורה פה בכלל. eman • שיחה • ♥ 00:41, 3 בדצמבר 2012 (IST)

אפס. שימור תנע בתוספת ההבחנה שכשהארגז בגובה המקסימלי הוא במנוחה ביחס לקורה. ירון ק. - שיחה 23:41, 21 בדצמבר 2012 (IST)

חידות

יש למישהו רעיון? יעלו עוד חידות בהמשך. ‏cheshin61‏ • שיחה • י"ט בכסלו ה'תשע"ג • 13:46, 3 בדצמבר 2012 (IST)

פתרתי בהנחה שהבנתי את החידה נכון. הכוונה שמפסיד מי שבתורו יש בערימה פחות מ-99 מולקולות כי אז הוא לא יכול לקחת כלום בלי שזה יהיה יותר מ-1%? אתה רוצה רמז או פתרון מלא? דניאל • תרמו ערך 18:35, 3 בדצמבר 2012 (IST)

אם יש 99 אז הפסדת, אם יש 100 ניצחת. הצלחתי לשחזר מה קורה עד 1000 מולקולות בערך אבל זה לא מקרב אותנו ל99!. בכל מקרה הדד ליין של הגשת התשובה עבר כבר, זה מאולימפיאדה למתמתיקה שהייתה היום בכל מיני אוניברסיטאות בעולם. אבל התשובה עדיין מסקרנת אותי. ‏cheshin61‏ • שיחה • כ' בכסלו ה'תשע"ג • 01:19, 4 בדצמבר 2012 (IST)

נגדיר ברקורסיה מספרים מנצחים ומספרים מפסידים. המספרים המפסידים הראשונים הם 1 עד 99. מעבר לכך: מספר מנצח הוא מספר שאם תורך לשחק וגודל הערימה הוא המספר, אז יש לך דרך לשחק כך שהערימה תקטן למספר מפסיד. מספר מפסיד יהיה מספר שלא משנה איך תשחק אתה בהכרח מקטין את הערימה למספר מנצח. עכשיו הכל מצטמצם לשאלה האם 99 עצרת הוא מספר מנצח או מספר מפסיד. אם הוא מספר מנצח אז השחקן הראשון יכול להבטיח נצחון (הוא יעביר ליריב את התור במספר מפסיד, שיחזיר לו את התור במספר מנצח וכן הלאה). אם 99 עצרת מספר מפסיד אז השחקן השני יקבל מספר מנצח והוא זה שינצח את המשחק. אז בוא אני אתן לך הזדמנות לסיים לבד. תוכיח שכל מספר שמתחלק ב-100 הוא מספר מנצח ולכן השחקן הראשון מנצח (99 עצרת מתחלק במאה כמובן). רמז: עד כמה ארוכה יכולה להיות סדרה של מספרים מנצחים רצופים הקטנים ממספר מסוים? אם הצלחת להבין מה קורה עד 1000 אז לדעתי אתה מסוגל לראות את ההוכחה של הטענה. דניאל • תרמו ערך 01:51, 4 בדצמבר 2012 (IST)

תודה רבה דניאל, מאוד עזרת לי, עכשיו אני יכול לישון בשקט.

רצף המספרים המנצחים עולה ב1 לכל מאה מספרים לכן הרצף מספרים זוכים יהיה :${\frac {99!}{100}}$. עוד קצת מחשבה ואני יסגר על זה. הייתי בכיוון הנכון ועזרת לי להתאפס על מה שקורה שם. תודה. ‏cheshin61‏ • שיחה • כ' בכסלו ה'תשע"ג • 09:17, 4 בדצמבר 2012 (IST)

לא בדיוק, הרצפים יכולים להציג התנהגות יותר מורכבת מזה. הטיעון הוא ככה: מהמספר $100k$ אפשר להגיע למספרים $100k-1,100k-2,\ldots ,100k-k$. כדי ש-$100k$ יהיה מספר מפסיד כל המספרים ברצף הזה חייבים להיות מספרים מנצחים. אבל זה לא ייתכן כי אפשר להגיע לאותם המספרים בדיוק מ-$100k-1$ ולכן הוא מספר מפסיד, וזו סתירה. מכאן ש-$100k$ מספר מנצח. דניאל • תרמו ערך 13:32, 4 בדצמבר 2012 (IST)

עכשיו הבנתי לגמרי. לא נראה לי שהייתי מגיע לזה לבד ב20 דקות שהיה לי לפתור את השאלה, אבל נהנתי מהשאלה הזאת. ‏cheshin61‏ • שיחה • כ"א בכסלו ה'תשע"ג • 14:42, 5 בדצמבר 2012 (IST)

זה לא מזכיר קצת נים? DoronWise - שיחה 17:14, 28 בדצמבר 2012 (IST)

מזכיר, אבל לא שקול. דניאל • תרמו ערך 17:15, 28 בדצמבר 2012 (IST)

היכולות להיות יחידות בתוך ln?

אני זוכר שאמרו לי שלא, אבל אני רואה עכשיו, גם בדוגמאות של מתרגלים שיש פתאום ln של מהירות, או מסה. מה התנאי? אביעד‏ • שיחה 17:02, 3 בדצמבר 2012 (IST)

התוכל להראות ביטוי מפורש כזה, עם ארגומנט הכולל מהירות או מסה ? סביר יותר להניח שהארגומנט כולל יחס בין מהירויות או מסות. בנצי - שיחה 17:19, 3 בדצמבר 2012 (IST)

כן. ההקשר הוא משוואה דיפרנציאלית שבאחד האגפים היה האינטגרל של dv/v, התשובה היא הרי ln(v). אביעד‏ • שיחה 17:49, 3 בדצמבר 2012 (IST)

טעית בביטוי האחרון שבסוף המשפט שלך. אל תשכח, שאינטגרל (לא מסויים) של נגזרת של פונקציה - אינו הפונקציה - אלא הוא הסכום של הפונקציה עם קבוע כלשהו. לכן, האינטגרל של dv/v אינו (ln(v אלא הוא ln(v)+c, כאשר c הוא קבוע כלשהו (שערכו יתגלה בהמשך). עכשיו שים לב: הרי במקום c אפשר לרשום (ln(u-, כאשר u הוא קבוע כלשהו (למשל אם c=1 אז u=1/e), וממילא מתקבל שיש קבוע u כך שהאינטגרל של dv/v הוא בעצם (ln(v)-ln(u, כלומר הוא בעצם (ln(v/u, כאשר v הוא משתנה המהירות, בעוד ש-u הוא קבוע המהירות. כדי לגלות מהו u יש להציב ערך התחלתי כלשהו של v שעבורו כבר ידוע מהו ערך האינטגרל dv/v (בדרך כלל ערך האינטגרל ידוע עבור v=0), וכך מתקבלת משוואה שמאפשרת לגלות את u. בשורה התחתונה, הלוגריתם אינו מופעל על v אלא על היחס שבין v לבין u, כלומר על יחס שבין שתי מהירויות: אחת משתנית ואחת קבועה. סמי20 - שיחה 18:50, 3 בדצמבר 2012 (IST)

תודה על הארת העיניים. עם זאת, הביטוי ln(v)+c עדיין מכיל בתוכו את ln(v), מדוע זה לא "נחשב" שיש יחידות ב-ln. ומעבר לכך, באילו מקרים צריך להוסיף קבועים - לא בדיוק הבנתי את החוקיות. כאשר אני עושה אינטגרל מסוים עם תחום מוגדר על dv/v, אני צריך קבוע? ומה לגבי המקרים כאשר אני עושה אינטגרל מסוים על dv, יש קבוע? תודה רבה, אביעד‏ • שיחה 20:05, 3 בדצמבר 2012 (IST)

לגבי שאלתך הראשונה: אכן אם v אינו מספר טהור - אלא כזה שיש בו יחידות, אז אלה שאוהבים לדייק - אינם כותבים שיש קבוע c כך שהאינטגרל של dv/v הוא ln(v)+c, אלא הם כותבים ישירות שיש קבוע u כך שהאינטגרל של dv/v הוא (ln(v/u. הסיבה שכתבתי לך שהאינטגרל של dv/v הוא ln(v)+c, היא משום שרציתי להבהיר את זה יותר "אינטואיטיבית" - לאור העובדה שאם v הוא מספר טהור נטול-יחידות אז באמת כן ניתן לכתוב במפורש שיש קבוע c כך שהאינטגרל של dv/v הוא ln(v)+c. אבל הדייקנים - שאינם סומכים על האינטואיציה - אלא מחפשים הוכחה מדויקת יותר לכך שאם v אינו מספר טהור (אלא כזה שיש בו יחידות) אז יש קבוע u כך שהאינטגרל של dv/v הוא (ln(v/u, נאלצים להתעמק יותר בכל המושג של האינטגרל ואיך הוא מוגדר - מה שמאריך את ההוכחה. לא עשיתי זאת כאן כי רציתי לחסוך בביטים.

לגבי שאלתך השניה: תמיד יש קבוע, אלא שאם מדובר באינטגרל מסויים (כגון שמדובר במציאת שטח מתוחם היטב מתחת לגרף של פונקציה שמהווה את הנגזרת של האינטגרל), אז עצם הוספת הקבוע אינה מעלה ואינה מורידה, שהרי האינטגראל המסויים מחושב כידוע ע"י פעולת הפרש (שבין שני ערכים מסויימים של פונקצית האינטגרל הלא מסויים) - מה שגורם מניה-וביה להתקזזות הקבוע (אל תשכח שההפרש שבין קבוע לבין עצמו הוא אפס). אבל אם מדובר באינטגרל לא מסויים, שכידוע - אינו מחושב כהפרש - אלא כפונקציית-אינטגרל (של פונקציה אחרת שמהווה את הנגזרת של פונקצית האינטגרל), אז באמת חובה להקפיד לציין את קיומו של הקבוע. אמנם הרבה טועים בכך, אבל הדייקנים לא טועים: אינטגרל (לא מסויים) של נגזרת של פונקציה - אינו הפונקציה - אלא הוא הסכום של הפונקציה עם קבוע כלשהו. אגב, כפי שכתבתי לך, ניתן לגלות את הקבוע, אם ידוע מראש ערכה של פונקצית האינטגרל עבור מספר כלשהו (למשל: במקרה שלך אנחנו מן הסתם כבר יודעים את ערכו של האינטגרל עבור v=0, מה שמאפשר לגלות את הקבוע). סמי20 - שיחה 21:52, 3 בדצמבר 2012 (IST)

בעקרון בכל פונקציה צריך להופיע ארגומנט ללא יחידות. ln הוא יוצא דופן, כנראה היחידי. הסיבה היא הזהות $\ln {\frac {a}{b}}=\ln a-\ln b$.

המשמעות היא שאם גם ל-a וגם ל -b יש אותן יחידות הביטוי של זה חלקי זה הוא חסר יחידות. אבל אז אם משתמשים בזהות, מקבלים חיסור של שני ביטויים שכאילו הם דווקא בעלי יחידות.

ועוד דרך להסתכל על אותו דבר הוא לומר שה-a זה הגודל, ו-b, זה רק היחידות. אז איכשהו הוא תמיד הוא יכול "להתחבא" שם... eman • שיחה • ♥ 22:23, 3 בדצמבר 2012 (IST)

תודה לשניכם. שורה תחתונה, אם מופיע לי במשוואה דיפרנציאלית אינטגרל של v/dv, או רק dv, בשניהם אני חייב לשים קבוע, גם אם האינטגרל מסוים? אביעד‏ • שיחה 23:27, 3 בדצמבר 2012 (IST)

אם האינטגרל מסויים אז אתה מקבל את הקבוע באופן אוטומטי. eman • שיחה • ♥ 00:05, 4 בדצמבר 2012 (IST)

נניח שאתה רוצה לקחת את האינטגרל המסויים של פונקצית הזהות Y=X בתחום שבין a לבין b: אז עליך להחסיר מ-b²/2+c את a²/2+c, מה שנותן לך את b²/2-a²/2, ומכאן שהוספת הקבוע לא מעלה ולא מורידה. אבל אם האינטגראל אינו מסויים אז חובה להקפיד על הקבוע. סמי20 - שיחה 00:59, 4 בדצמבר 2012 (IST)

כן, אבל מי אמר שההקבועים הם אותם הקבועים בכל צד של המשוואה? אלו פונקציות שונות. אביעד‏ • שיחה 16:35, 4 בדצמבר 2012 (IST)

גם אם זה נכון, הרי שבמונחים של יחידות הם כן. בנצי - שיחה 04:34, 5 בדצמבר 2012 (IST)

יש לך פונקציה אחת. הקבוע הוא אותו קבוע. דניאל • תרמו ערך 13:18, 5 בדצמבר 2012 (IST)

זה לא שהקבועים הם אותם קבועים, אלא שאתה מציב בערכים של גבולות האינטגרל ערכים מתואמים, ואז הכל מסתדר. כלומר עם באינטגרציה של הצד עם ה dt הגבול התחתון הוא אפס, והעליון הוא t, אז באינטגרציה על הצד של dv הגבול התחתון הוא $v_{0}$, והעליון הוא $v(t)$. eman • שיחה • ♥ 13:38, 5 בדצמבר 2012 (IST)

אביעד, דניאל צודק. הקבוע הזה הוא באמת - כשמו - קבוע, שאינו משתנה. אילו הוא היה משתנה (ושלא כשמו), אז הנגזרת שלו לא היתה פונקצית-האפס, וממילא הפונקציה המקורית שעבורה מחושבת פונקצית-האינטגרל - לא היתה יכולה להיות הנגזרת של פונקצית-האינטגרל של הפונקציה המקורית (בְּדוֹק). סמי20 - שיחה 15:17, 20 בדצמבר 2012 (IST)

ממוצע עבור סדרה רציפה שהנתונים שלה מקובצים

שלום רב,

איך אני מחשב ממוצע כאשר יש לי מספר קבוצות (שוות גודל) וידוע לי כמה נתונים יש בכל קבוצה (למנוע אי הבנה: נניח ציונים עד 60 - 0 תלמידים, 60-70 - 8 תלמידים, 70-80 - 20 תלמידים, 80-90 - 17 תלמידים, 90-100 5 תלמידים)

על תשובתכם אודה, יגאל.

בהנחה שהנתונים מתפלגים באופן אחיד בתוך כל קבוצה, מחשבים את הממוצע המשוקלל כאילו כל הנתונים היו ממוקמים באמצעי הקבוצות. כלומר: 8*65+20*75+17*95+4*5, לחלק לגודל הכתה. עוזי ו. - שיחה 20:06, 4 בדצמבר 2012 (IST)

האם הרביע כולל בתוכו גם את הציר שמשיק לו?

זאת אומרת- האם הנקודה (3,0) נמצאת גם על הרביע הראשון והרביעי או שהיא על אף רביע? האם ראשית הצירים נמצאת בכל ארבעת הרביעים? תודה למי שישיב מתן – שיחה – 19:38, 4 בדצמבר 2012 (IST)

זו שאלה של הגדרה. אני הייתי מגדיר את הרביעים כקבוצות פתוחות, כלומר ללא הצירים. עוזי ו. - שיחה 20:07, 4 בדצמבר 2012 (IST)

בהרחבה לעוזי, אפשר לדבר על רביע סגור (הוא קבוצה סגורה) שכולל את הצירים, ואפשר לדבר על רביע פתוח ללא הצירים (הוא קבוצה פתוחה). דניאל • תרמו ערך 20:16, 4 בדצמבר 2012 (IST)

משוואות דיפרנציאליות

איך אני פותר את המשוואות הנ"ל כאשר נתונים r_0,V_0=0, omega=constant:

${\ddot {r}}=r\omega ^{2}-gsin(\omega t)$

${\dot {r}}={\frac {N}{2\omega m}}-{\frac {g\cos(\omega t)}{2\omega }}$

תודה, אביעד‏ • שיחה 22:06, 4 בדצמבר 2012 (IST)

נראה לי שאפשר לגזור את השניה בזמן ולהציב בראשונה. ירון ק. - שיחה 23:43, 21 בדצמבר 2012 (IST)

מערכת מד"ר

אלפה ובטה זה פונקציות של הזמן. קיבלתי 2 משוואות:

• $-\gamma \beta (t)=i{\frac {\partial \alpha }{\partial t}}$
• $-\gamma \alpha (t)=i{\frac {\partial \beta }{\partial t}}$

i זה אלמנט מדומה, גאמה קבוע בזמן. איך אני פותר את המערכת? 109.67.201.187 22:42, 4 בדצמבר 2012 (IST)

משוואה ראשונה - גזור את שני האגפים לפי t, והכפל ב-i. משוואה שנייה - הכפל בגאמא. אגף שמאל של המשוואה הראשונה שווה לאגף ימין של השניה. 80.230.25.130 05:25, 5 בדצמבר 2012 (IST)

שאלה זו או דומה לה, כבר הופיעה ב'הכה' לפני כמה חודשים, אבל לא זוכר בדיוק מתי. בנצי - שיחה 17:28, 5 בדצמבר 2012 (IST)

שאלה שקשורה לתנועה זוויתית.

יש בסירטון הזה (בדקה 1:40) משפט שלא ממש הבנתי, על יחס בין סינוס זווית כידון האופניים לריבוע המהירות הזוותית והמסה. אשמח להסבר קצר. ‏cheshin61‏ • שיחה • כ"א בכסלו ה'תשע"ג • 17:44, 5 בדצמבר 2012 (IST)

לדעתי אין במשפט הזה כוונה פיזיקלית של ממש. אפשר לבצע בדיקת יחידות ולראות שסינוס הוא מספר טהור ומהצד השני ישנן יחידות שלא מצטמצמות. מצד שני, ייתכן שיש כאן התייחסות למשוואה אחרת כלשהיא שלא מוכרת לי ולא מצאתי בחיפוש מהיר בגוגל. Amirber - שיחה 22:04, 9 בדצמבר 2012 (IST)

רדיוס שוורצשילד

האם מה שכתוב בסוף הערך רדיוס שוורצשילד נכון? שכל קוף הקטן מרדיוס שוורצשילד שלו הוא חור שחור? 79.176.253.92 17:54, 6 בדצמבר 2012 (IST)

יותר הגיוני "כל גוף". למרות שכל קוף הוא גוף אבל לא כל גוף הוא קוף. ‏cheshin61‏ • שיחה • כ"ג בכסלו ה'תשע"ג • 20:44, 6 בדצמבר 2012 (IST)

התשובה היא כן (אני מניח שהכוונה למילה "גוף"). ‏Setreset • שיחה 22:40, 8 בדצמבר 2012 (IST)

אלקטרוניקה תיאורטית / חשמל

מה קורה אם מחברים סוללה אידאלית (ללא התנגדות פנימית) לעצמה באמצעות תיל אידאלי (חסר התנגדות)? האם התיל ישרף? אם כן, ליד איזה מהדקי הסוללה הוא ישרף?--46.117.105.50 17:55, 6 בדצמבר 2012 (IST)

אי אפשר להתייחס לחוט אידיאלי כי חייב להיות לו מוליכות\התנגדות מסויימת. בפועל אם תיקח בטריה רגילה, היא תתפרק לגמרי תוך זמן קצר (תלוי במוליכות ובעובי החוט) אבל לא תישרף. כדי לדעת מתי ישרף החוט, אפשר לבדוק לפי הנוסחה $\,p_{m}=v^{2}\cdot \sigma$, כאשר $\,p_{m}$ הוא ההספק המקסימלי של הבטריה ו$\sigma$ היא מוליכות החוט. לגבי מיקום השריפה זאת שאלה באמת עניינת, אין לי מושג אבל הייתי מנחש שאיזור הפריצה יהיה קרוב יותר לצד החיובי. (התשובה בעירבון מוגבל, אני עדיין סטודנט). ‏cheshin61‏ • שיחה • כ"ג בכסלו ה'תשע"ג • 21:14, 6 בדצמבר 2012 (IST)

אם החוט אידיאלי ואין לו התנגדות אז הוא מוליך על, והוא לא יתחמם, ולא יישרף. ‏Setreset • שיחה 22:39, 8 בדצמבר 2012 (IST)

ומה אם נדרוש מהתיל רק להיות בעל התנגדות ועובי אחידים?--46.117.105.50 17:51, 10 בדצמבר 2012 (IST)

יזרום זרם בחוט, והוא יתחמם. למה שיישרף? אם השאלה איפה הוא מתחמם הכי הרבה, אז אני לא רואה למה דווקא ליד אחד מההדקים. זה יקרה לפי אי-אחידויות בחוט, איזור שבו במקרה יש התנגדות גדולה יותר או קוטר חוט קטן יותר, או שהחוט קיבל מכה באזור. ‏Setreset • שיחה 21:25, 10 בדצמבר 2012 (IST)

תודה. הנחתי שהתיל ישרף עקב הזרם הגדול שיעבור דרכו, ומפה נובע שהוא צריך להתחמם יותר דווקא היכן שהתנגדותו נמוכה יותר -- איפה הטעות?46.117.105.50 22:13, 10 בדצמבר 2012 (IST)

נראה לי שאתה חושב על החוט כאילו הוא רצף של חוטים שכל אחד מהם מחובר לסוללה זהה. אם זה היה כך, היית צודק. אבל זה לא המקרה, כי יש רק סוללה אחת, והזרם העובר בחוט הוא קבוע לכל אורך החוט. עבור זרם קבוע, הספק חום גדול יותר יהיה כאשר ההתנגדות גדולה יותר. ‏Setreset • שיחה 09:21, 11 בדצמבר 2012 (IST)

האם כל היסודות יכולים להיות בכל מצב צבירה?

האם כל היסודות יכולים להיות בכל מצב צבירה? 95.35.65.9 19:37, 6 בדצמבר 2012 (IST)

ציטוט מהערך מצב צבירה (מההתחלה שלו):

"לא כל החומרים מופיעים בכל מצבי הצבירה, לדוגמה: נייר לא יכול להיות גז, הוא נשרף, משנה את מבנהו הכימי והופך לפיח. מים כדוגמה, הם חומר המסוגל להיות בכל ארבעת מצבי הצבירה."

רצוי לבדוק ולחפש תשובה, לפחות חיפוש קצר, במרחב הערכים לפני ששואלים פה. ‏cheshin61‏ • שיחה • כ"ג בכסלו ה'תשע"ג • 21:20, 6 בדצמבר 2012 (IST)

נייר זה לא יסוד כימי והוא שאל על יסודות. בברכה, MathKnight (שיחה) 21:29, 6 בדצמבר 2012 (IST)

לפי w:List of elements כל היסודות עוברים התכה ורתיחה. על פחמן כתוב שהוא עובר רק המראה (כלומר אין פחמן נוזלי), אך זה לא מדויק לפי המאמר הזה. נשארת האפשרות שישנם איזוטופים "שחסר להם" מצב צבירה, אך זה לא סביר לדעתי. חשדתי שאין הליום-3 מוצק, ויש. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

אכן הייתי קצת פזיז. עימך הסליחה. ‏cheshin61‏ • שיחה • כ"ג בכסלו ה'תשע"ג • 02:46, 7 בדצמבר 2012 (IST)

יצויין שקיימים מצבים כמו "פלאזמה", "על נוזל" ו"על מוצק". 109.67.196.69 11:06, 7 בדצמבר 2012 (IST)

ההיסטוריה של הזכוכית קשה להבנה בויקיפדיה

בערך זכוכית: "בני אדם השתמשו ויצרו להבים מזכוכית געשית הנקראת אובסידיאן כבר בתקופת האבן. השתמשו בה ליצור סכינים וראשי חצים, במזרח אפריקה נמצאו עדויות להעברת חומר הגלם למרחק ניכר ממקום החציבה כבר בתקופת האבן התיכונה לפני כ-30,000 שנים‏[1]. יצור של זכוכית על ידי בני אדם התחיל כ-3-4 אלף שנה לפני הספירה. בשריפה של זרעים האפר שנישאר מהשריפה התחבר עם החול בטמפרטורה גבוהה ונוצרה זכוכית סיליקטית המכילה 60% SiO2. בהוספה של אשלגן חמצני K2O אפשר לקבל זכוכית שקופה. אנשים השתמשו בזכוכית הזאת ליצור תכשיטים ובקבוקונים."

1. כיצד זה אמור לענות לי על השאלה כיצד עשו זכוכית בעבר (לפני אלף או אלפיים שנה)? האם היה להם (או האם הם ידעו מהו) אשלגן חמצני K2O (זו שאלה רטורית כמובן).

2. בעבר מן הסתם יצרו זכוכית שקופה, א"כ איך יצרו אותה בלי לקבל תואר ראשון בכימיה.

3. לא מוסבר מדוע שרפו דווקא זרעים בשביל לקבל אפר, הרי אפשר לשרוף חומרים רבים שהיו בשימוש (כמו צואה ועצים לדוגמה) ולקבל מהם אפר.

אשמח לקבל תשובות על השאלות הנ"ל, תודה 176.13.203.165 16:23, 7 בדצמבר 2012 (IST)

אני לא מומחה לעניין הספציפי הזה, אבל כאשר אין בסיס מדעי מסודר לתהליך כלשהו, משיגים תוצאות מעולות גם עם ניסוי וטעיה בלבד. בעצם, ככה גם מגיעים לתוצאות מדעיות בסופו של דבר, כאשר הניסוי וטעיה נעשים בצורה שיטתית. הם פשוט ניסו להוסיף כל מני חומרים, ובמקרה (או בעקבות מאמץ שיטתי) קיבלו תוצאות טובות. אני יכול לשער שדווקא זרעים שימשו לזכוכית כי זה מגיע בגדלים קטנים וזהים שמאפשרים ערבוב טוב ומדויק מאוד עם החול. כאשר אין כלים תעשייתיים קשה להשיג שבבי עץ בגודל קטן וזהה. זה גם מאמץ מיותר, כאשר יש זרעים שהם באים כבר מוכנים. כאמור, אלו השערות שלי על פי נסיון בתהליכים קרמיים אחרים. ‏Setreset • שיחה 22:36, 8 בדצמבר 2012 (IST)

מכניקת הקוונטים והסתברות שלמה

פה שאלה ופתרונה( מתחיל בצד שמאל. דילגתי על כל הפיתרון עד לסעיף שלא הבנתי). אני מבין את הנוסחה של נוסחת ההסתברות השלמה. אבל לא מבין מאיפה לקחו את הנתונים, כלמור מה החישוב שעשו בשביל להגיע לתוצאה של $0.5|c_{1}|^{2}+0.5|c_{2}|^{2}$. 79.182.197.54 21:04, 8 בדצמבר 2012 (IST)

שאלה לגבי חיכוך ומשוואה דיפרנציאלית

גוף נע בתווך שכוח החיכוך עשפועל עליו יחסי לריבוע מהירותו $\left|f\right|=bv^{2}$. המהירות ההתחלתית היא $v_{0}$. ניתן להניח כי אין כבידה. יש למצוא את מהירות החלקיק כפונ' של הזמן, ולאחר מכן להראות מפורשות כי העבודה המוצעת על ידי כוח החיכוך עד לעצירות הגוף שווה לאנרגיה הקינטית ההתחלתית.

תחילה הגעתי למשוואה דיפרנציאלית ופתרתי אותה: ${\frac {dv}{dt}}=-{\frac {bv^{2}}{m}}\Rightarrow v={\frac {v_{0}m}{m+bv_{0}t}}$

ראשית איני בטוח כי הפתרון נכון. וב' חישוב העבודה נראה לי בעייתי כאן. כי כשניסיתי לחשב את אורך המסלול לצורך חישוב העבודה, קיבלתי, והדבר די הגיוני שהוא אינסופי... איפה הפשלה? אביעד‏ • שיחה 08:29, 10 בדצמבר 2012 (IST)

הפתרון נכון, ולא אמורה להיות בעיה עם העבודה - היא לא מתבדרת. חשב ע"פ $W=\int fdx=\int f{\frac {dx}{dt}}dt=\int _{0}^{\infty }fvdt$; באינטגרנד המתקבל לאחר הצבה של המהירות והכח יש במכנה ביטוי מהצורה $(a+bt)^{3}$. אינטגרל זה מתכנס כמובן. בהצלחה.

אחלה, תודה. אביעד‏ • שיחה 19:57, 10 בדצמבר 2012 (IST)

חישוב נגזרות חלקיות ללא יעקוביאן

נתונות הפונקציות: $F(u,v,x,y)=2yu-xv^{3}-4x,G(u,v,x,y)=xu^{2}+v-y^{3}$

כיצד ניתן לחשב את ${\frac {\partial v}{\partial y}}$ ואת ${\frac {\partial u}{\partial y}}$ כאשר x מוחזק בשתי הנגזרות, ללא יעקוביאן, באמצעות גזירה? אביעד‏ • שיחה 14:25, 10 בדצמבר 2012 (IST)

נוסחה עם אויילר וסינק

איך עושים את המעבר${\frac {|1-e^{i\omega t}|^{2}}{\omega ^{2}}}=t^{2}sinc^{2}({\frac {\omega }{2}}t)$?79.176.202.60 19:35, 10 בדצמבר 2012 (IST)

מפרקים את המונה. ירון • שיחה 20:26, 10 בדצמבר 2012 (IST)

$\ |1-cos(wt)-isin(wt)|^{2}=(1-cos(wt))^{2}+(sin(wt))^{2}=1-2cos(wt)+cos^{2}(wt)+sin^{2}(wt)=2-2cos(wt)=4sin^{2}(wt/2)$

מהירות זוויתית

שלום,

אני מנסה לכתוב סימולציה של עריסתו של ניוטון. נתקעתי בעניין פעוט: אחרי שהתוכנה מחשבת את וקטורי המהירויות של הכדורים לאחר התנגשות, אני מקבל שני וקטורים [Vx,Vy] (אחד לכל כדור), שהם וקטורי המהירות הקווית של הכדורים לאחר ההתנגשות, ומהם מסיק את המהירות הזוויתית לאחר ההתנגשות. הענין שאני לא בטוח לגביו הוא: כיצד מוצאים את כיוון המהירות הזוויתית (עם או נגד כיוון השעון) לאחר ההתנגשות, על בסיס וקטור המהירות הנ"ל? תודה, 94.159.185.194 21:39, 10 בדצמבר 2012 (IST)

מכפלה וקטורית עם וקטור הזרוע. הסימן של הרכיב היחידי קובע את כיוון הסיבוב. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

תודה רבה. 94.159.185.194 15:30, 11 בדצמבר 2012 (IST)

ניסוי בפיזיקה

בשיעור פיזיקה ערכנו ניסוי. כל תלמידי המגמה עמדו במעגל ונתנו ידיים זה לזה. התלמיד הראשון והתלמיד האחרון נגעו בסוללה חזקה. הזרם עבר דרך כל התלמידים, והדליק את הנורה. רציתי לשאול, האם האלקטרונים שקודם היו בכף היד שלי עברו לכתף, אלקטרונים שהיו בכתף עברו לחזה, וכו'? האם כעת יש לי בגוף אלקטרונים שהיו בגוף של תלמיד אחר? האם יש סכנה בניסוי כזה? איך פעולה כזאת משפיעה על הגוף? 87.68.166.35 04:03, 11 בדצמבר 2012 (IST)

אכן, אלקטרונים עברו מתלמיד לתלמיד. אנחנו כל הזמן מחליפים מולקולות עם הסביבה - בנשימה, אכילה ושתיה, וגם אחקטרונים, בכל מיני פעילויות חשמליות - כמו במכה של חשמל סטטי (כשמחשמלים אחד את השני). הניסוי יכול להיות בטוח אם המתח נמוך, או עלול להיות מסוכן אם המתח גבוה מדי, השאלה היא איזה מתח היה בסוללה בניסוי שלכם. בנוסף, המתח של הסוללה מתחלק על פני כל התלמידים שהחזיקו יד בטור. ‏Setreset • שיחה 08:58, 11 בדצמבר 2012 (IST)

האלקטרונים אמנם זזים, אבל מרחקים קטנים בהרבה מהמתואר. האלקטרונים לא עושים את כל הדרך מהיד לכתף. מדובר במרחקים מיקרוסקופיים. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

שאלה לגבי תנע ומרכז מסה

התקשיתי בדרך הגישה לשאלה זו. להבנתי, כשהכדור באחד מהקצוות ומהירות 0, המוט בשיא מהירותו, אך כיצד נראית תנועה מרכז המסה, ומה השפעתה? איך ניתן לפתור את התרגיל. אשמח לעזרה.

גוף בעל מסה M תלוי בעזרת חישוקים חסרי מסה על גבי גליל חלק. מוט חסר מסה שאורכו l מחובר בצדו האחד לכדור מסה m ובצדו האחר לציר חלק העובר דרך מרכזו של הגוף M כמתואר בשרטוט. משחריים את הכדור בזווית theta0 ביחס לאנך והמערכת מתחילה לנוע.

א. מצאו את היחס בין המהירות האופקית של המסה M לבין המהירות האופקית של המסה m.

ב. בטאו את האנרגיה הקינטית והאנרגיה הפוטנציאלית של המערכת, כתלות בזוית תטא ובנגזרת של לפי הזמן תטא(דוט). (השתמשו במרכז המסה של המערכת).

ג. הראו שעבור זוויות קטנות מתקבלת תנועה הרמונית וחשבו את תדירות התנועה, כלומר הראו שמתקבלת המשוואה ${\ddot {\theta }}+\omega ^{2}\theta =0$

תודה, אביעד‏ • שיחה 19:09, 11 בדצמבר 2012 (IST)

האם אני מבין נכון, והגוף בעל המסה M חופשי לנוע אך ורק בציר האופקי? משה פרידמן - שיחה 10:19, 12 בדצמבר 2012 (IST)

זה לא נתון, אבל נראה לי לי שאין בעיה שהוא ינוע כמו מטוטלת. אביעד‏ • שיחה 19:17, 12 בדצמבר 2012 (IST)

תנע בהתנגשות פלסטית

אם אני זורק פלסטלינה על קיר והיא נדבקת אז אין שימור של תנע, נכון? איך זה מסתדר? 79.181.200.198 16:01, 12 בדצמבר 2012 (IST)

יש שימור של תנע. המסה של הפלסטלינה זניחה ביחס לזו של הקיר (שמחובר לבניין שבתורו מחובר לאדמה), ולכן לא רואים את מעבר התנע. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

ההשפעה של התנע תהייה במעיכה של הפלסטלינה על הקיר, ככל שהתנע יותר גדול, מרכז המסה של הפלסטלינה יהיה קרוב יותר לקיר בסוף התהליך. ‏cheshin61‏ • שיחה • א' בטבת ה'תשע"ג • 04:02, 14 בדצמבר 2012 (IST)

זה דווקא מתכונתי לאנרגיה הקינטית ולא לתנע. דהיינו מתכונתי לריבוע המהירות ולא למהירות. ―אנונימי לא חתםמש:אנונימי ‌ 00:00, 10 בינואר 2000 (IST)

שמש מסתובבת סביב כ"א

שאלה בגאומטריה: נניח לצורך העניין שכדור הארץ הוא נקודתי ולא חג סביב עצמו. המודל הרגיל הוא הסתכלות על השמש כנייחת, כלומר שנקודת "כדור הארץ" נעה במעגל סביב נקודת "השמש". עכשיו - איך נראית התנועה מנקודת המבט של כדור הארץ? 192.114.105.254 13:16, 13 בדצמבר 2012 (IST)

השמש נעה במעגל (בעל אותו רדיוס) סביב כדור הארץ, באותה מהירות ובאותו כיוון. עוזי ו. - שיחה 13:47, 13 בדצמבר 2012 (IST)

השמש עושה סיבוב פעם בשנה. היום נמשך חצי שנה והלילה נמשך חצי שנה. ‏Setreset • שיחה 21:04, 13 בדצמבר 2012 (IST)

איזה חלק בפיזיקה כדאי ללמוד קודם?

אני רוצה ללמוד פיזיקה אבל יש כמה חלקים בפיזיקה: מכניקה, קרינה, חשמל, אופטיקה. עם איזה חלק מתחילים או מומלץ להתחיל? 176.13.63.32 16:51, 13 בדצמבר 2012 (IST)

כולם מתחילים במכניקה כך שנראה לי שזה הנושא הראשון. -יונה בנדלאק - שיחה 19:05, 13 בדצמבר 2012 (IST)

מכניקה->חשמל->קרינה-> אופטיקה. 79.183.247.5 19:42, 13 בדצמבר 2012 (IST)

האם אפשר לשאול מה גיל השואל ומה סיבת הלימוד? סתאם לידע כללי או כהכנה לקורסים אקדמיים? אני ממליץ בחום על שלושה ספרים עבי כרס בשם "מבינים פיזיקה" בנושאים מכניקה, חשמל ופיזיקה מודרנית, אם יש לך גישה לספריה רצינית. בלינק המצורף אפשר גם לראות חלקים מעניינים מהספרים. ‏cheshin61‏ • שיחה • א' בטבת ה'תשע"ג • 04:02, 14 בדצמבר 2012 (IST)