טרפז
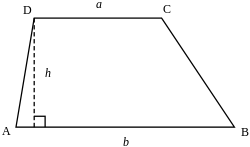
בגאומטריה, טְרָפֶּז (באנגלית: trapezoid או trapezium) הוא מרובע בעל זוג צלעות נגדיות מקבילות אחד בלבד. שתי הצלעות המקבילות נקראות "בסיסי הטרפז" (לפעמים קרויה "בסיס" רק הצלע הארוכה יותר), ושתי האחרות "שוקי הטרפז". בטרפז ניתן להמשיך את שוקי הטרפז עד שהן ייפגשו בנקודה, ובצורה זו נוצר משולש המכיל את הטרפז. הזוויות הסמוכות לכל אחד מהבסיסים נקראות זוויות הבסיס.
על פי הגדרה נוספת ("הגדרה מרחיבה"), הטרפז הוא מרובע בעל לפחות זוג אחד של צלעות נגדיות מקבילות. לפי הגדרה זו, במקרה שבו גם שוקי הטרפז מקבילות, המקבילית היא מקרה פרטי של טרפז. הגדרה זו מתאימה לשימושים שונים במתמטיקה גבוהה.
אטימולוגיה
[עריכת קוד מקור | עריכה]מקור המונח "טרפז" במונח היווני τραπέζιον, טרפזיון, שמשמעותו "שולחן קטן". זוהי צורת ההקטנה של τράπεζα, טרפזה, שמשמעותו "שולחן". גם המילה "טרפזה" מורכבת משתי מילים: τετράς, טטרס (ארבע) ו-πέζα, פזה (רגל), כלומר "טרפזה" משמעו "בעל ארבע רגליים".
תכונות של טרפז
[עריכת קוד מקור | עריכה]
- מרובע הוא טרפז אם ורק אם יש לו שתי זוויות סמוכות שסכומן 180 מעלות.
- סכום הזוויות הנמצאות על אותה שוק הוא 180 מעלות
- היחס בין החלקים של האלכסונים שווה ליחס בין הבסיסים:
- קטע אמצעים בטרפז, הוא קטע אשר מחבר בין אמצעי שוקי הטרפז. קטע האמצעים בטרפז מקביל לבסיסי הטרפז ואורכו הוא ממוצע האורכים שלהם.
- הזווית בין הצלע לאלכסון שווה לזווית שבין הצלע הנגדית לאותו אלכסון.
- האלכסונים חותכים את המרובע לארבעה משולשים שמתוכם לזוג אחד מנוגד יש שטחים שווים.
- מכפלת השטחים של שני המשולשים הנוצרים על ידי אלכסון אחד שווה למכפלת שטחי שני המשולשים הנוצרים על ידי האלכסון השני.
שטח
[עריכת קוד מקור | עריכה]את שטח הטרפז ניתן לחשב כמכפלת המרחק בין שתי הצלעות המקבילות (זהו גובה הטרפז) והממוצע החשבוני של אורך הצלעות הללו. כך ניתן להגיע לנוסחה הידועה של שטח משולש, כאשר אנו מחשיבים את המשולש כטרפז בו אחת הצלעות המקבילות מכווצת לנקודה בודדת (כלומר בעלת אורך 0). נוסחאות לחישוב שטח טרפז כלשהו (כאשר a,b מציינים בסיסים; ו-c,d מציינים צלעות):
- או
כאשר a,b,c,d צלעות טרפז.
האלכסונים יוצרים ארבעה משולשים: מכפלת שטח שני המשולשים הנוצרים עם הבסיסים שווה למכפלת שטח שני המשולשים הנוצרים עם השוקיים.
טרפזים מיוחדים
[עריכת קוד מקור | עריכה]טרפז נקרא שווה-שוקיים אם שתי השוקיים שלו שוות זו לזו באורכן. בטרפז שווה-שוקיים מתקיים כי שתי זוויות הבסיס שוות זו לזו וכן שני האלכסונים שווים.
כל טרפז החסום במעגל הוא שווה-שוקיים משום שסכום הזוויות הנגדיות בכל מרובע החסום במעגל שווה ל-180 מעלות (וכן סכום זוויות סמוכות בטרפז שווה ל-180 מעלות) .

טרפז נקרא ישר-זווית אם יש לו שתי זוויות השוות כל אחת ל-90 מעלות. במקרה זה, גובה הטרפז הוא השוק עליה נשענות שתי הזוויות הישרות.
לטרפז חד זווית יש שתי זוויות חדות צמודות בקצה הבסיס הארוך יותר שלו.
לטרפז קהה זווית לעומת זאת, יש זווית חדה אחת ואחת קהה בכל בסיס.
טרפז משיק הוא טרפז בעל מעגל חסום.
חסרונות ההגדרה מצמצמת לטרפז
[עריכת קוד מקור | עריכה]בהגדרת הטרפז לעיל נעשה שימוש בהגדרה "המצמצת" של טרפז, כלומר, הגדרת טרפז כ"מרובע שבו יש זוג יחיד של צלעות המקבילות זו לזו" (או, "מרובע אשר לו זוג אחד בלבד של צלעות מקבילות"). מגוון מקורות העוסקים בגאומטריה (ובהם האנציקלופדיה העברית והאתר של משרד החינוך בישראל[1]) משתמשים בהגדרה זו. הגדרה זו מוציאה את המקבילית ממשפחת הטרפזים, ויש לה מספר חסרונות בולטים:
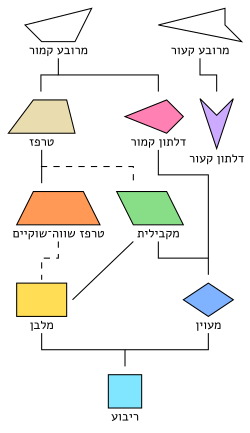
- בעוד שכל ריבוע הוא סוג מיוחד של מלבן וכל מעוין הוא סוג מיוחד של דלתון, הרי על-פי ההגדרה המצמצמת, המקבילית איננה טרפז. בין משפחות המרובעים שוררים יחסי הכלה, וההגדרה המצמצמת הופכת את הטרפזים לחריג.
- שוויון הנכון לכל הטרפזים (במובן הצר) נכון תמיד גם עבור מקביליות. ההגדרה שהובאה בתחילת הערך מאפשרת לנסח את שתי התוצאות במשפט אחד, בעוד שבהגדרה המצמצמת יש צורך לחזור על הטענה (וההוכחה) פעמיים.
- כל סוגי המרובעים מוגדרים על-פי שוויון (צלעות שוות, זוויות שוות, זווית ישרה), ורק הגדרה מצמצמת של הטרפז תדרוש אי-שוויון.
- הסעת קודקוד אחד של הטרפז לאורך אחת הצלעות המקבילות תשמור על תכונות הטרפז עד ששניים מקודקודיו מתלכדים. הגדרה מצמצמת תוסיף לתהליך כזה נקודה מיוחדת שבה הטרפז חדל לרגע מלהיות טרפז - תופעה שאין לה אח ורע במשפחות המרובעים האחרות (וגם לא בהגדרות גאומטריות כלליות יותר).
עם כל זאת, יודגש שהשאלה איזו הגדרה "נכונה" יותר היא תלוית הקשר. כלומר, הגדרה נבחנת בכך שהיא מפשטת את הדיון במונחים שאליהם היא מתייחסת.
שימושים
[עריכת קוד מקור | עריכה]הטרפז משמש בתחומים שונים, בהם מתמטיקה, פיזיקה והנדסה, בשל תכונותיו הגאומטריות הייחודיות.
בתחום המתמטי, הטרפז משמש לחישוב שטחים בשיטות נומריות, כגון שיטת הטרפז, המשמש להערכת שטחים מתחת לעקומות במסגרת אינטגרציה נומרית.
בגרפיקה ממוחשבת נעשה שימוש בצורת הטרפז לצורך יצירת עיוותי פרספקטיבה ואפקטים ויזואליים נוספים.
בהנדסה, צורת הטרפז תורמת לעמידות מבנים כמו גשרים ותמיכות, בזכות בסיסיו השונים המסייעים לחלוקת עומסים יציבה.
באדריכלות המילה משמשת להתייחסות לדלתות, חלונות ומבנים סימטריים הבנויים רחבים יותר בבסיסם, מתחדדים לכיוון העליון, בסגנון מצרי. אם לאלה יש צדדים ישרים ופינות זוויתיות חדות, הצורות שלהם הן בדרך כלל טרפז שווה שוקיים. זה היה הסגנון הסטנדרטי של הדלתות והחלונות של האינקה.
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- הגדרות שונות ל"אותו מושג" – מנוף או מכשול? המקרה של הטרפז, קרני שיר ואורית זסלבסקי, על"ה 54 | אוגוסט 2016
- טרפז, באתר MathWorld (באנגלית)
הערות שוליים
[עריכת קוד מקור | עריכה]
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |



