מספר ממשי

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

במתמטיקה, מספר ממשי הוא כל מספר רציונלי או אי רציונלי במערכת המספרים, כגון $\ 3,-4.1,{\tfrac {1}{3}}$או $\ 2\pi$. בעזרת מספרים ממשיים ניתן למדוד גדלים רציפים, כגון טמפרטורה, מרחק, וכו'.

ניתן לראות את המספרים הממשיים החיוביים כאורכים של קטעים על ישר אינסופי (הקרוי, לפיכך, הישר הממשי). לכל מספר חיובי מתאים גם מספר שלילי באותו גודל, המודד את אותו קטע בכיוון ההפוך.

קיימת התאמה בין הישר הממשי למספרים הממשיים, כך שכל מספר ממשי מייצג נקודה אחת ויחידה על הישר הממשי וכל נקודה על הישר הממשי מייצגת מספר ממשי אחד ויחיד.

ניתן למקם כל מספר ממשי על הישר הממשי

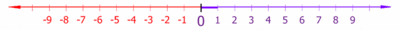
על המספרים הממשיים ניתן להגדיר פעולות חיבור וכפל שהופכות אותם למבנה אלגברי הקרוי שדה. שדה זה נקרא שדה המספרים הממשיים ומסומן על ידי $\mathbb {R}$. בנוסף, מוגדר על הממשיים יחס סדר טבעי לפי מיקומם על הישר הממשי. שתי תכונות אלו יחדיו הופכות את קבוצת המספרים הממשיים לשדה סדור שלם.

בעזרתם של המספרים הממשיים מוגדרים מושגים יסודיים במתמטיקה בכלל ובחשבון הדיפרנציאלי והאינטגרלי בפרט, כגון: גבול, רציפות, אינטגרל, חסם עליון ונגזרת.

השם "מספר ממשי" ניתן למספרים אלה במאה ה-17 על ידי הפילוסוף והמתמטיקאי הצרפתי רנה דקארט.

היסטוריה והתפתחות

התפיסה לפיה קיימות נקודות רבות בין מספרים רציונליים, כמו השורש הריבועי של 2, הייתה מוכרת היטב ליוונים הקדמונים. קיומו של ישר מספרים רציף נחשב מובן מאליו, אך טבעה של המשכיות זו, הנקראת כיום שלמות, לא הובן. המתודולוגיה הריגורוזית שפותחה עבור הגאומטריה לא עברה למושג המספרים עד למאה ה-19.

עבור מתמטיקאים יוונים, מספרים היו רק המספרים הטבעיים. מספרים ממשיים נקראו "פרופורציות", שהם היחסים של שני אורכים, כלומר, מידות של אורך במונחים של אורך אחר, הנקרא יחידת אורך. שני אורכים הם "ניתנים להשוואה", אם יש יחידה שבה שניהם נמדדים במספרים שלמים, כלומר, בטרמינולוגיה המודרנית, אם היחס שלהם הוא מספר רציונלי. אאודוקסוס מקנידוס (בערך 390-340 לפנה"ס) סיפק הגדרה לשוויון של שתי פרופורציות אי-רציונליות באופן הדומה לחתכי דדקינד (שהוכנסו יותר מ-2,000 שנים מאוחר יותר). ניתן לראות זאת כהגדרה הראשונה של המספרים הממשיים.

ימי הביניים הביאו את קבלתם של אפס, מספרים שליליים, מספרים שלמים ושברים, תחילה על ידי מתמטיקאים הודים וסינים, ולאחר מכן על ידי מתמטיקאים ערבים, שהיו גם הראשונים להתייחס למספרים אי-רציונליים כעצמים אלגבריים (האחרונים התאפשרו על ידי התפתחות האלגברה).

השם "מספר ממשי" ניתן למספרים אלה במאה ה-17 על ידי דקרט, שעשה זאת כדי להבחין בין שורשים ממשיים לבין שורשים מדומים של פולינום. בפיתוחו של החשבון האינפיניטסימלי במאה ה-18 נעשה שימוש נרחב במספרים ממשיים, אף על פי שלא הייתה עדיין הגדרה נאותה שלהם.

התיאורים הבלתי פורמליים לעיל של המספרים הממשיים אינם מספיקים כדי להבטיח את נכונותן של הוכחות למשפטים הכוללים מספרים ממשיים. ההבנה שדרושה הגדרה טובה יותר, והפיתוח של הגדרה כזו היו התפתחות מרכזית של המתמטיקה של המאה ה-19. ב-1872 פרסם גאורג קנטור מאמר שבו הגדיר את המספרים הממשיים באמצעות סדרות קושי של מספרים רציונליים; הגדרתו (השקולה) של ריכרד דדקינד את המספרים הממשיים באמצעות חתכי דדקינד פורסמה מעט מאוחר יותר באותה שנה.

מספרים רציונליים ואלגבריים

דוגמאות לייצוג של מספרים ממשיים כנקודות על הישר הממשי

לאחר שקובעים את אורכה של יחידה המידה היסודית, האורך של מספר יחידות כאלה נקרא מספר שלם. מספר ממשי שאפשר לבטא כיחס בין שני מספרים שלמים נקרא מספר רציונלי, אך רוב המספרים הממשיים אינם כאלה. עוצמתה של קבוצת המספרים הממשיים היא עוצמת הרצף שאיננה בת מנייה (כפי שהוכח באמצעות האלכסון של קנטור), ואילו אוסף המספרים הרציונליים הוא בן-מנייה. המספרים הממשיים שאינם רציונליים, כגון שורש 2, $\ \pi$ או e, נקראים אי-רציונליים. את קבוצת המספרים האי-רציונליים אפשר לחלק לשתי תת-קבוצות:

• קבוצת המספרים האלגבריים: מספרים המהווים שורש של פולינום בעל מקדמים רציונליים (או שלמים, אין הבדל). זו קבוצה בת מנייה.
• קבוצת המספרים טרנסצנדנטיים: מספרים שאינם מספרים אלגבריים. זו קבוצה שאינה בת מנייה ועוצמתה היא עוצמת הרצף. קיומם של מספרים טרנסצנדנטיים הוכח לראשונה בשנת 1844 על ידי המתמטיקאי הצרפתי ז'וזף ליוביל והתוצאה קרויה על שמו משפט ליוביל. בשנת 1882 הוכיח פרדיננד לינדמן את משפט לינדמן שקובע, בין השאר, ש־$\ \pi$ (פאי) הוא מספר טרנסצנדנטי.

לכל מספר ממשי אי-שלילי יש שורש ריבועי ממשי, ולכל מספר ממשי שלילי אין שורש ריבועי ממשי. למספרים שליליים יש שורש מדומה. למעשה, השורשים באים בזוגות: אם $a>0$ אז $x=\pm {\sqrt {a}}$ שניהם שורשים ממשיים של $a$ ואם $b<0$ אז $y=\pm i{\sqrt {|b|}}$ שניהם שורשים מדומים של $b$. באופן כללי, הפתרון של משוואה ריבועית הוא שני מספרים מרוכבים (כולל ריבוי). כל מספר ממשי הוא גם מספר מרוכב.

ההצגה העשרונית

כל מספר ממשי אפשר להציג כשבר עשרוני, בעל מספר סופי או אינסופי של ספרות מימין לנקודה. לחלק מהמספרים הרציונליים הייצוג כשבר עשרוני הוא סופי (למשל: 0.5=1/2), ולאחרים - אינסופי ומחזורי, למשל: ...0.08536585365=7/82 (מחזור בן 5 ספרות).

מספרים שהם שברים עשרוניים סופיים ניתנים להצגה כשברים אינסופיים בשתי דרכים:

• הוספת כמות אינסופית של אפסים אחרי הספרה העשרונית האחרונה. למשל: ...32.4800000000000 = 32.48
• כיוון ש-0.999... שווה ל-1, ניתן לרשום גם ....65.299999999999 = 65.3

למספרים האי-רציונליים הייצוג כשבר עשרוני אינו מחזורי. למשל, $\pi$ הוא מספר טרנסצנדנטי, והייצוג העשרוני שלו אינו מחזורי. חמישים הספרות הראשונות הן $\pi =3.14159\,26535\,89793\,23846\,26433\,83279\,50288\,41971\,69399\,37510\ldots$. לצרכים מעשיים ניתן להסתפק בדיוק נמוך יותר, ומקובל להסתפק בקירובים 3.14 או 3.14159.

מרחק וטופולוגיה

המרחק בין שני מספרים על הישר הממשי מוגדר כערך המוחלט של הפרשם.

בטופולוגיה, קבוצת המספרים הממשיים יוצרת מרחב מטרי, שבו המרחק בין $x$ ל-$y$ מוגדר כערך המוחלט $|x-y|$. בדרך זו התאמתם של המספרים הממשיים לנקודות על הישר הממשי מאפשרת לבטא את אורכו של כל קטע במישור.

על פי תכונת ארכימדס, לכל מספר ממשי קיים מספר טבעי שגדול ממנו. נובע מכאן שהמרחב המטרי של המספרים הממשיים הוא מרחב ספרבילי, משום שקבוצת המספרים הרציונליים, שהיא בת מנייה, היא קבוצה צפופה (שכן כל קטע פתוח מכיל מספר רציונלי). הארכימדיות מאפשרת להגדיר את הערך השלם של $x$, בתור המקסימום של $\{n\in \mathbb {Z} \mid n\leq x\}\!$.

לפי אקסיומת ארכימדס אם מניחים עותקים של קטע קצר בזה אחר זה, בסופו של דבר אפשר יהיה לעבור קטע אחר הארוך ממנו. מכאן ניתן להוכיח שלכל מספר ממשי קיים מספר טבעי שגדול ממנו.

ראו גם

• התפתחות מושג המספר
• בניית המספרים הממשיים

קישורים חיצוניים

• גדי אלכסנדרוביץ', מהם המספרים הממשיים?, באתר "לא מדויק", 7 בספטמבר 2010
• גדי אלכסנדרוביץ', אז מה זה בעצם המספרים הממשיים? (חלק א': השיטה העשרונית), באתר "לא מדויק", 11 באוגוסט 2024
• מספר ממשי, באתר MathWorld (באנגלית)
• מספר ממשי, באתר אנציקלופדיה בריטניקה (באנגלית)