מתנד הרמוני
מַתְנֵד הרמוני (או אוסצילטור הרמוני, מאנגלית: Harmonic oscillator) הוא מערכת מכנית שבה פועל על גוף נתון כוח מתכונתי (יחסי) להעתק הגוף ובכיוון מנוגד לו: , כאשר הוא הכוח, הוא קבוע המתנד ו- הוא ההעתק. כוח זה נקרא גם כוח מחזיר שמשמעותו היא כוח שתמיד פועל לכיוון נקודת שיווי המשקל.
באנלוגיה, כל מערכת פיזיקלית שמאופיינת מתמטית בצורה דומה נקראת אף היא "מתנד הרמוני". חשיבותו של מודל המתנד ההרמוני נובעת מכך שתופעות פיזיקליות רבות מתוארות על ידי מערכות שמתנהגות, ברמות קירוב שונות, כמתנד הרמוני. לדוגמה, מסה התלויה על קפיץ, מעגלים חשמליים מסוימים, גלים בחומר, מיתרי גיטרה או כלי פריטה אחר, ואפילו גלי אור במובן מסוים. במובן זה המתנד ההרמוני הוא מודל פיזיקלי המתאים בקירוב למקרים מגוונים רבים.
מתנד הרמוני, בפרט מתנד הרמוני פשוט, הוא אחת המערכות הפשוטות והבסיסיות ביותר בפיזיקה. זוהי מערכת פתירה באופן אנליטי כמעט בכל תורה פיזיקלית (מכניקה קלאסית, תרמודינמיקה, מכניקת הקוונטים, תורת היחסות ועוד) המשמשת ככלי עזר חשוב בלימוד התאוריות השונות והבנתן. יתרה מכך, מסתבר שניתן לקרב מערכות רבות ומורכבות - שאינן פתירות באופן אנליטי או פשוט - על ידי מתנדים הרמוניים, ובכך להגיע להבנה רבה ואף לפתרון מקורב לבעיה.
כאן נסקור את בעיית המתנד ההרמוני במכניקה הקלאסית. בנוגע לטיפול במתנד הרמוני מאולץ, כלומר מתנד שפועל עליו כוח חיצוני המשתנה בתדירות שונה משל המתנד, ראו: תהודה.
בנוגע לטיפול במתנד הרמוני לפי מכניקת הקוונטים ראו: מתנד הרמוני קוונטי.
מתנד הרמוני פשוט
[עריכת קוד מקור | עריכה]
מתנד הרמוני פשוט, הוא מערכת בה פועל כוח מחזיר בלבד, שכן כשמו הוא מנסה להחזיר את המערכת לנקודת שיווי המשקל שלה, לאחר שזו סטתה ממנו. באופן כללי משוואת המתנד ההרמוני היא משוואה דיפרנציאלית מהצורה כאשר הוא הגודל המחזורי, ו- הוא הנגזרת השנייה בזמן של הגודל המחזורי.
במכניקה הקלאסית, כוח מחזיר, הוא כוח מהצורה כאשר הוא קבוע המאפיין את המערכת כמו קבוע הקפיץ בחוק הוק, ו- הוא העתק המסה מנקודת שיווי המשקל.
ניתן לרשום את החוק השני של ניוטון עבור המערכת הבנויה ממסה המחוברת לקפיץ, תוך כדי כתיבת התאוצה בדרך מעט שונה :
. נשים לב, כי המסה תסומן באות . מקובל לחלק את שני אגפי המשוואה ב- ולהגדיר , כך שלאחר העברת אגפים מתקבלת המשוואה .
לגודל יש יחידות של תדירות, והוא מקיים את התכונות הבאות:
- הוא ממשי ומוגדר היטב, היות שהמסה וקבוע הקפיץ תמיד חיוביים;
- הוא גודל קבוע, היות שהמסה או קבוע הקפיץ אינם משתנים, לפי הגדרת המערכת (אם המסה הייתה יכולה להשתנות, משוואת הכוחות שממנה פותחה המשוואה הדיפרנציאלית אינה מתאימה, והמשוואה הדיפרנציאלית תהיה שונה).
משוואה זו היא משוואה דיפרנציאלית ליניארית הומוגנית מסדר שני, שניתן לפתור באמצעות הפולינום האופייני של המערכת: , אשר שורשיו הם הצמד , כאשר הוא היחידה המדומה. בדרך כלל, כאשר משתמשים בפולינום האופייני לפתרון משוואה דיפרנציאלית, הפתרון יהיה מהצורה . עם זאת, על ידי הצבת הפתרונות של הפולינום האופייני, מתקבל במשוואה זו הפתרון , שהוא פונקציה מרוכבת – כלומר, אינו פונקציה ממשית, בעוד ההעתק הוא גודל ממשי.
הבעיה נפתרת אם דורשים כי , כלומר, ששני המספרים הם צמודים זה לזה. למשל, אם , אז , ואז לפי נוסחת אוילר,
פירוש פיזיקלי של הפתרון
[עריכת קוד מקור | עריכה]מכיוון שפונקציית הקוסינוס (בערך מוחלט) לא עולה מעבר ל־, הגודל שסימנו באות מאפיין את נקודות ההתרחקות המקסימלית של המערכת מנקודת שיווי המשקל. גודל זה יקרא משרעת (אמפליטודה) ולרוב יחושב מתנאי ההתחלה. למשל, אם ידוע שקפיץ נמתח באורך מסוים, אורך זה יהיה המשרעת.
המופע (פאזה) שסומן באות , יילקח גם הוא מתנאי ההתחלה. גודל זה מאפיין את ההזזה של פונקציית הקוסינוס. מבחינה פיזיקלית, המופע שונה מאפס, אם מדידת הזמן החלה לא בדיוק ברגע בו שוחררה המסה ממנוחה.
לשם הפשטות, ניתן לבחון מקרה פשוט יותר של המתנד, בו אין מופע (). במקרה כזה, העתק המסה נתון על ידי המשוואה . היות שהפונקציה המתארת את העתק המסה היא פונקציה טריגונומטרית, ניתן להסיק כי התנועה מחזורית. אם כך, קיים זמן מינימלי הדרוש כדי שהמערכת תשלים מחזור אחד (תבצע תנועה אחת שלמה) ותחזור לאותה הנקודה בה התחילה. המחזור של פונקציית הקוסינוס הוא , ולכן נדרוש שכאשר נציב את לתוך הפונקציה, הארגומנט של הפונקציה, יהיה שווה ל־. כלומר, נדרוש שיתקיים .

הזמן נקרא זמן המחזור של התנועה: , והתדירות של המערכת, לפי הגדרתה מקיימת . בגלל הקשר המיוחד בין התדירות לגודל , מקובל לקרוא ל- תדירות זוויתית. התדירות הזוויתית – וממילא גם התדירות "הרגילה" – נקבעות אך ורק על ידי מאפייני המערכת, ואינן תלויות בזמן או בגדלים משתנים אחרים.
לאחר שהתקבל פתרון המתאר את תנועת המסה במרחב, מתקבלת המהירות כפונקציה של הזמן מתוך גזירת משוואת התנועה; ועל ידי גזירה פעם נוספת, תתקבל התאוצה. כלומר, שלוש המשוואות אשר יתארו את התנועה הן:
אנרגיה
[עריכת קוד מקור | עריכה]כעת, נרצה לדבר על האנרגיה של המערכת. עבור מסה המחוברת לקפיץ, סך האנרגיה נתון על ידי סכום של אנרגיה קינטית של המסה כפונקציה של הזמן, ואנרגיה פוטנציאלית אלסטית כפונקציה של הזמן. על ידי הצבת הגדלים שמצאנו למשוואת האנרגיה, מתקבל:
כלומר, התלות בזמן מתבטלת, והאנרגיה זהה בכל זמן. במילים אחרות, האנרגיה במערכת נשמרת.
במערכת שנותחה עד כאן, הגורם לתנודות היה הקפיץ. אך קיימות מערכות נוספות, ללא קפיץ, בהן יכולות להיות תנודות. גם במקרים כאלה האנרגיה נשמרת, מכיוון שכוח מחזיר הוא כוח משמר. כלומר, העבודה שלו אינה תלויה במסלול, והרוטור של כוח זה, שווה לאפס. ניתן להוכיח זאת עבור כל כוח מחזיר.
מתוך משוואות שימור האנרגיה, ניתן לראות שכאשר כל האנרגיה הפוטנציאלית מתאפסת, האנרגיה הקינטית מקסימלית. למעשה, הנקודה בה האנרגיה הפוטנציאלית מתאפסת, היא בדיוק נקודת שיווי המשקל (באנלוגיה של הקפיץ, האנרגיה הפוטנציאלית מתאפסת כאשר הקפיץ רפוי). לכן, המהירות מקסימלית, בנקודת שיווי המשקל.
במכניקה הקלאסית, משוואת המתנד ההרמוני יכולה להיות משוואת מומנטים (היא מתקבלת על ידי בחירת נקודה קריטית במערכת לא נקודתית לרוב וכתיבת כל מומנטי הכוח הפועלים ממנה, תוך כדי מתן תשומת לב לכיוון המומנט. בדרך משוואת מומנטים תוביל אותנו למשוואת מתנד על זווית כלשהי במערכת כפונקציה של הזמן), משוואת כוחות (היא מתקבלת בדרך כלל על ידי כתיבת החוק השני של ניוטון על מערכת של נקודה אחת לרוב) או משוואת אנרגיה גזורה (היא מתקבלת על ידי גזירת המשוואה המתארת את האנרגיה של המערכת והשוואתה לאפס. ניתן לעשות זאת, בגלל שימור האנרגיה. היות שהאנרגיה נשמרת, היא שווה לקבוע כלשהו שנעלם בעת הגזירה).
מתנד הרמוני מרוסן
[עריכת קוד מקור | עריכה]
בתיאור הקודם, הנחנו כי אין חיכוך במערכת. נראה איך מתנהג המתנד במקרה בו יש חיכוך.
חיכוך הוא כוח מרסן נפוץ בטבע - חיכוך עם האוויר או עם נוזל, התנגדות של מעגל חשמלי, ועוד. כוח משכך זה תלוי ביחס ישר במהירות (נקרא גם כוח סטוקס). נניח לדוגמה כי כוח החיכוך נגרם על ידי בוכנת אוויר, כבאיור, ונניח כי הכוח מתכונתי למהירות הגוף ונתון על ידי , כאשר הוא מקדם הפרופורציה.
כעת משוואת הכוחות נראית כך: . על ידי סידור אלגברי מקבלים או
, כאשר , כמקודם.
מתנד הרמוני פשוט הוא מקרה פרטי של מתנד הרמוני מרוסן, בו .
בהנחה שהחיכוך קטן מספיק, הפתרון הכללי למשוואה זו הוא:
, כאשר:
- , הוא הזמן האופייני של המערכת. זהו הזמן בו משרעת התנודה דועכת בפקטור e.
- , היא תדירות התנועה המרוסנת.
- הביטוי , הוא משרעת התנודה, הדועכת באופן מעריכי עם הזמן.
פתרון מפורט מופיע בהמשך הערך. זוהי תנודה הרמונית, המתבצעת בתדירות נמוכה מעט מהתדירות הטבעית (תמיד מתקיים ). במערכת זו, בניגוד לתנודה ההרמונית הפשוטה, יש איבוד אנרגיה מתמיד לחיכוך.
אם החיכוך גדול מדי, התנועה תדעך מהר מאוד, באופן מעריכי, כך שלא יסתיים אפילו מחזור תנודה יחיד. קיים ערך מקסימלי של שיכוך (ריסון), שבערכי שיכוך גדולים ממנו לא יתרחשו כלל תנודות. ערך זה נקרא השיכוך הקריטי, והוא נתון על ידי .
פתרון המשוואות
[עריכת קוד מקור | עריכה]הניתוח המובא פה הוא למקרה המתואר למעלה: מסה מחוברת לקפיץ בעל קבוע , עם מקדם חיכוך (כאמור, מתנד הרמוני פשוט הוא מקרה פרטי שבו מתקיים ) . המשוואה המתארת את המצב היא:
זוהי משוואה דיפרנציאלית הומוגנית וליניארית, מסדר שני. במשוואות מסוג זה, מרחב הפונקציות המקיימות את המשוואה הוא מרחב וקטורי מממד 2. לכן מספיק למצוא שתי פונקציות (בלתי תלויות) שמקיימות את המשוואה - הן יהיו בסיס שלם למרחב כל הפתרונות האפשריים. מנחשים פתרון מהסוג , (המקדם יכול להיות מרוכב). כאשר מציבים את הפונקציה הזו במשוואה, ולפי תכונת האקספוננט, , מתקבל פולינום ממעלה שנייה שפתרונו פשוט: .
זוהי משוואה ריבועית שפתרונותיה הם . כאן . מכיוון שהפתרונות יכולים להיות מרוכבים, יש תמיד פתרון למשוואה. אם אין חיכוך, ואז .
כעת ישנם שלושה מקרים מובחנים:
- אם , ישנו פתרון ממשי שלילי עבור . הפתרון למקרה הכללי הוא חיבור של שתי פונקציות אקספוננציאליות דועכות:
- זהו מצב של שיכוך-קריטי, שבו לא יתרחשו תנודות, אלא התנועה תדעך לאפס. התנאי לשיכוך קריטי הוא שהדיסקרימיננטה תהיה אפס, משמע , כלומר .
- אם , ישנם שני פתרונות ממשיים שליליים עבור . הפתרון למקרה הכללי הוא חיבור של שני פונקציות אקספוננציאליות דועכות:
- זהו מצב של שיכוך-יתר, שבו לא יתרחשו תנודות, אלא התנועה תדעך לאפס. התנאי לשיכוך יתר הוא שהדיסקרימיננטה תהיה חיובית, משמע , כלומר .
- אם , מתקבלים שני פתרונות מרוכבים צמודים. זהו המקרה השכיח יותר, וממילא גם המעניין יותר, שבו השיכוך קטן ולכן מתרחשות תנודות הרמוניות דועכות. בהצבת פתרונות המשוואה הריבועית, ושימוש בנוסחת אוילר, מקבלים את שני הפתרונות למשוואה הדיפרנציאלית:
- לשם נוחות, נסמן .
- פתרון המשוואה הכללי הוא מהצורה . כאן ו- הם קבועים כלשהם, התלויים בתנאי ההתחלה של הבעיה. כיוון שרק פתרון ממשי הוא פיזיקלי, נדרש (הקו העליון מסמן צמוד מרוכב). מאחר שמתקיים ממילא , חייב להתקיים . כך מתקבל פתרון ממשי טהור מהצורה
- .
- כל המקדמים בביטוי הם ממשיים, ולכן ניתן לפשט את הסכום לביטוי יחיד המכיל מופע:
- .
- כאן הן המופע והמשרעת ההתחלתיים, הנקבעים על ידי תנאי ההתחלה של הבעיה. פתרון זה מתאר תנודה הרמונית בתדירות זוויתית
- עם משרעת דועכת בזמן. מכיוון שלמקדם יש יחידות של , נהוג להגדיר את הזמן האופייני .
כאשר אין חיכוך, ולכן ומקבלים את הביטוי המוכר של תנודה הרמונית פשוטה: .
דוגמאות נוספות למערכות שמקיימות תנודות הרמוניות
[עריכת קוד מקור | עריכה]מטוטלת
[עריכת קוד מקור | עריכה] ערך מורחב – מטוטלת מתמטית
ערך מורחב – מטוטלת מתמטית
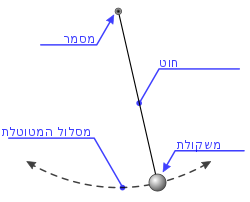
מטוטלת מתמטית פשוטה היא מערכת שמקיימת תנועה הרמונית רק בקירוב. תנועתה המלאה היא מחזורית וסוטה במקצת מתנועה הרמונית, אך בקירוב זוויות קטנות אפשר להתייחס לתנועתה כתנועה הרמונית.
נניח שמסת המטוטלת היא והיא מחוברת לתקרה בחוט אידיאלי חסר משקל באורך בתוך שדה כבידה אחיד . נסמן ב- את הזווית בין המטוטלת לאנך.
הכוח המחזיר יהיה הרכיב של כוח הכובד בכיוון המשיק לתנועה הרדיאלית של המטוטלת, כלומר: . לכן, משוואת התנועה תהיה:
בקירוב של זוויות קטנות , ומאחר ש- נשאר קבוע, מקבלים את משוואת התנועה:
זוהי תנועה הרמונית רק בקירוב, שכן משוואת התנועה הייתה רק קירוב למשוואת התנועה המדויקת. במקרה של מטוטלת אפשר לפתור באופן אנליטי גם את המשוואה הלא-ליניארית; הפתרון הוא אינטגרל אליפטי. גם מטוטלת שאינה מורכבת ממסה נקודתית מקיימת תנודה הרמונית בקירוב. למעשה, כל גוף בעל מסה התלוי מנקודה אחת מהווה מתנד הרמוני. מטוטלת כזו נקראת מטוטלת פיזיקלית.
מעגל LC
[עריכת קוד מקור | עריכה]מעגל LC אידיאלי (ללא התנגדות) הוא מעגל המכיל קבל ומשרן, בו האנרגיה האלקטרומגנטית עוברת בין הקבל למשרן באופן מחזורי הרמוני.

מכך שהמתח הכללי על המעגל הוא אפס (על פי חוקי קירכהוף) ניתן להסיק כי:
כאשר:
ומאחר ש־, נובע כי:
, ולכן וכאן תדירות התנועה היא .
מעגל RLC
[עריכת קוד מקור | עריכה]מעגל RLC, הוא מעגל זהה למעגל LC, בתוספת נגד. מעגל שכזה הוא מתנד הרמוני מרוסן, כיוון שהוא מקיים את המשוואה:
.
מבחינה מתמטית, מעגל RLC שקול למתנד הרמוני מרוסן הבנוי ממסה המחוברת לקפיץ עם שיכוך תלוי מהירות, כמו זה שהוצג למעלה. האנלוגיה למתנד מכני היא:
| מתנד מכני | מתנד חשמלי |
| מסה () | השראות הסליל () |
| קבוע הקפיץ () | 1 חלקי הקיבול () |
| העתק () | מטען חשמלי () |
| מהירות () | זרם () |
| שיכוך () | התנגדות () |
הכללות של מתנד הרמוני
[עריכת קוד מקור | עריכה]המתנד ההרמוני מצטיין בתכונה הבסיסית שזמן המחזור של חלקיק שתונד הרמונית אינו תלוי במשרעת. לא משנה כמה רחוק החלקיק ישוחרר ממרכז הכוח של המתנד, הוא תמיד ישלים תנודה באותו זמן. תכונה זו אינה נכונה כאשר דנים בחוקי כוח אחרים בהם הכוח לא יחסי למרחק מהמרכז - משפט ידוע קובע שאם התלות של זמן המחזור במשרעת היא מהצורה (כאשר היא המשרעת ו- הוא קבוע פרופורציה) אז הכוח המרכזי הוא מצורה . למשל אם (זמן המחזור לא תלוי במשרעת) נקבל: , כלומר נקבל מתנד הרמוני. יותר מכך, אם נציב נקבל , כלומר נקבל כוח היפוך-ריבוע - במקרה פרטי זה קיבלנו את החוק השלישי של קפלר. חישוב קבוע הפרופורציה בביטוי לזמן המחזור לפי המשרעת לרוב כרוך בחישוב אינטגרל מסובך ולעיתים אין לו פתרון אנליטי.
ראו גם
[עריכת קוד מקור | עריכה]- תהודה
- תורת התנודות
- אנליזת פורייה: טור פורייה והתמרת פורייה
- מתנד הרמוני קוונטי
- אופני תנודה עצמיים
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- פתרון המד"ר
- מתנד הרמוני, באתר אנציקלופדיה למתמטיקה (באנגלית)
| גלים | ||
|---|---|---|
| מאפיינים | משרעת • תדירות • מופע • אורך גל • וקטור גל • מספר גל • מהירות פאזה • מהירות חבורה • קיטוב | 
|
| תופעות | החזרה • העברה • שבירה • התאבכות • עקיפה • נפיצה • בליעה | |
| מושגים | גל עומד • אפנון • חבילת גלים • תווך • מתנד הרמוני • תהודה • אפקט דופלר | |
| אנליזה | משוואת הגלים • משוואת הלמהולץ • עקרון הויגנס • עקרון פרמה • חוקי פרנל | |
| סוגי גלים | גל מישורי • גל כדורי • גל רוחב • גל אורך • פולס • קרינה אלקטרומגנטית • גל קול • גל (מים) • פונקציית גל | |

























![{\displaystyle {\begin{aligned}x(t)&=\alpha e^{\lambda _{1}t}+\beta e^{\lambda _{2}t}\\&={\frac {A}{2}}e^{i(\omega _{0}t+\phi )}+{\frac {A}{2}}e^{-i(\omega _{0}t+\phi )}\\&=\left[{\frac {A}{2}}\cos(\omega _{0}t+\phi )+{\cancel {i{\frac {A}{2}}\sin(\omega _{0}t+\phi )}}\right]+\left[{\frac {A}{2}}\cos(\omega _{0}t+\phi )-{\cancel {i{\frac {A}{2}}\sin(\omega _{0}t+\phi )}}\right]\\&=A\cos(\omega _{0}t+\phi )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f9f2a289e726addf7969c505c0216d6df15de6)



























































































