פונקציית גמא

פונקציית גמא היא פונקציה מרוכבת מֶרוֹמורפית, המרחיבה את מושג ה"עצרת" לכל המישור המרוכב: לכל מספר טבעי $\ n=1,2,\dots$, הפונקציה מקבלת את הערך $\ \Gamma (n)=(n-1)!$.

הפונקציה הוגדרה לראשונה על ידי לאונרד אוילר באמצע המאה ה-18, אך הסימון של הפונקציה באות $\ \Gamma$ נכנס לשימוש בעקבות עבודתו של לז'נדר. גאוס הציע גרסה מעט שונה של פונקציית גמא, $\ \Pi (z)=\Gamma (z+1)$, לה הוא קרא "פונקציית פאי", אלא שהסימון של לז'נדר הועדף בצרפת, ובעקבות זאת גם בשאר העולם.

הפונקציה מוגדרת במחצית הימנית של המישור המרוכב באמצעות האינטגרל $\Gamma (z)=\int _{0}^{\infty }t^{z-1}\,e^{-t}\,\mathrm {d} t$.

לפונקציית גמא קטבים (פשוטים) בנקודות $\,z=0,-1,-2,\dots$ בלבד, ואין לה שורשים. הפונקציה מקיימת את המשוואה הפונקציונלית $\ \Gamma (z+1)=z\Gamma (z)$, המסבירה את הקשר לפונקציית העצרת, ועוד זהויות פונקציונליות רבות אחרות.

הגדרה

פונקציית גמא מוגדרת על ידי האינטגרל הבא:

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}\,e^{-t}\,\mathrm {d} t$

וזאת לכל $\ z\in \mathbb {C}$ שהחלק הממשי שלו, $\,Re(z)$, הוא חיובי. פונקציה זו מתלכדת עם הפונקציה המוגדרת באמצעות הגבול $\ \Gamma (z)=\lim _{n\rightarrow \infty }{\frac {1\cdot 2\cdots n}{z\cdot (z+1)\cdots (z+n-1)}}(n+1)^{z-1}$, המוגדר היטב לכל $\ z\neq 0,-1,-2,\dots$. משום כך, הפונקציה השנייה מהווה המשכה אנליטית של האינטגרל לפונקציה מרומורפית.

תכונות

הקשר לפונקציית עצרת

גרף של פונקציית גמא על הישר הממשי

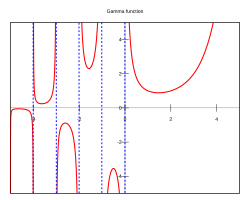
ניתן להראות שעבור מספרים טבעיים, פונקציית גמא שווה (בהזזת 1) לפונקציית העצרת.

אם $\,n$ הוא חיובי ושלם, אזי $\Gamma (n)=\int _{0}^{\infty }t^{n-1}\,e^{-t}\,\mathrm {d} t=(n-1)!$, כי על ידי ביצוע אינטגרציה בחלקים, אפשר להראות כי $\,\Gamma (n+1)=n\Gamma (n)$, ומאחר ש-$\,\Gamma (1)=1$ נקבל כי $\,\Gamma (n+1)=n\Gamma (n)=\ldots =n!\Gamma (1)=n!\,$ לכל מספר טבעי $\,n$.

זהויות אחרות

זהות חשובה אחת לפונקציית גמא היא נוסחת השיקוף: $\ \Gamma (1-z)\Gamma (z)={\pi \over \sin \pi z}$.

מכאן נובע כי $\Gamma \left({\frac {1}{2}}\right)^{2}={\pi \over \sin \pi /2}=\pi$, ולכן $\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}$.

זהות חשובה אחרת היא נוסחת הכפל של גאוס:

$\Gamma (z)\;\Gamma \left(z+{\frac {1}{k}}\right)\;\Gamma \left(z+{\frac {2}{k}}\right)\cdots \Gamma \left(z+{\frac {k-1}{k}}\right)=(2\pi )^{(k-1)/2}\;k^{1/2-kz}\;\Gamma (kz)\,\!$

גרף של הערך המוחלט של פונקציית גמא במישור המרוכב.
באיור זה ניתן לראות בבירור את הקטבים של הפונקציה

לפונקציית גמא יש קוטב ב $\,z=-n$ לכל $\,n$ טבעי. בנקודה זאת נתון גם ש:

$\operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}.$

המכפלה האינסופית הבאה, כפי שהראה ויירשטראס, נכונה לכל $\,z$ מרוכב, אשר אינו שלם אי-חיובי:

$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}$

כאשר $\,\gamma$ הוא "קבוע אוילר-מסקרוני".

משפט בוהר-מולרופ

ערך מורחב – משפט בוהר-מולרופ

משפט בוהר-מולרופ הוא משפט המאפיין את פונקציית גמא על פי המשוואה הפונקציונלית שהיא מקיימת. המשפט קרוי של-שמם של המתמטיקאים הדנים הארלד בוהר ויוהאן מולרופ שהוכיחו אותו.

משפט: פונקציית גמא הממשית, המוגדרת לכל $\,x>0$ על ידי $\Gamma (x)=\int _{0}^{\infty }t^{x-1}e^{-t}\,\mathrm {d} t$, היא הפונקציה היחידה $\,f$ בקרן $(0,\infty )$ המקיימת:

1. $\,f(1)=1$
2. $f(x+1)=xf(x)\ {\mbox{for}}\ x>0$
3. $\,f$ היא פונקציה לוג-קמורה

אחת ההוכחות לנוסחת סטירלינג משתמשת במשפט זה. במסגרת ההוכחה בונים פונקציה המקיימת את שלושת התנאים במשפט בוהר-מולרפ, ולכן פונקציה זו היא בהכרח פונקציית גמא.

אומדן

ערך מורחב – נוסחת סטירלינג

השוואה בין גמא מוזז (קו כחול) לעצרת (נקודות כחולות) ואומדן סטירלינג (קו סגול)

ניתן לאמוד את הערכים הממשיים והמרוכבים של פונקציית גמא בעזרת אומדן לנקזוס או אומדן סטירלינג:

$\Gamma (z)\sim {\sqrt {2\pi }}z^{z-1/2}e^{-z},\quad \left|\arg(z)\right|<\pi$

אומדן זה מדויק בכך שהיחס בין האומדן לערך האמיתי שואף ל-1 כש $|z|$ שואף לאינסוף.

ראו גם

• פונקציית בטא
• פונקציית גמא הלא שלמה
• משפט בוהר-מולרופ

קישורים חיצוניים

מדיה וקבצים בנושא פונקציית גמא בוויקישיתוף

• פונקציית גמא באתר Wolfram mathworld
• פונקציית גמא, באתר אנציקלופדיה למתמטיקה (באנגלית)
• מחשבון לפונקציית גמא
• פונקציית גמא, באתר MathWorld (באנגלית)
• פונקציית גמא, באתר אנציקלופדיה בריטניקה (באנגלית)