עץ מאוזן

עץ מאוזן
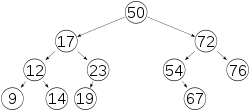דוגמה לעץ מאוזן (במקרה זה מסוג AVL המקיים את תכונת האיזון)
סיבוכיות מקום וזמן
	ממוצע במקרה הגרוע
זיכרון:	O(n) O(n)
חיפוש:	O(log n) O(log n)
הכנסה:	תלוי במימוש תלוי במימוש
הוצאה:	תלוי במימוש תלוי במימוש

עץ מאוזן הוא רעיון של מבנה נתונים מסוג עץ חיפוש בינארי, עץ חיפוש יקרא עץ מאוזן אם הגובה של העץ יהיה שווה ל- $\log _{2}(n)$ של (כאשר $\ n$הוא מספר הצמתים בעץ). כלומר עבור עץ $\ T$ וגובה $\ h$ אז העץ יהיה מאוזן אם: $\ h(T)$ = $\ O(\log n)$

תכונה זו מבטיחה שניתן יהיה לחפש בעץ בסיבוכיות של $\ O(\log n)$ במקרה הגרוע ביותר.

מהלך פעולה

עץ מאוזן כשלעצמו איננו מבטא מבנה נתונים בעל דרך להגיע למצב זה, אלא רעיון כללי לעץ שעבורו מתקיימים הדרישות ומכך גם מתקיימת תכונת החיפוש ב - $\ O(\log n)$. והוא בדומה לעץ בינארי מייצג קבוצה מסוימת המקיימת תכונה מסוימת (בהתאם) עבור מבנה נתונים.

תתי עצים

פותחו כמה מודלים מסוג עצי חיפוש בינארים המקיימים את התכונה הזו, ובניהם:

• עץ AVL
• עץ אדום שחור
• ערימת פיבונאצ'י

כל עץ מבצע פעולה הנקראת "איזון" על מנת להמשיך לקיים את דרישות העץ המאוזן. לדוגמה: עבור עץ AVL פעולת האיזון נקראת "גלגול".

משפטים

רשימת משפטים הנכונים עבור כל עץ המקיים את תכונת עץ מאוזן:

• עץ מנוון לעולם איננו יהיה עץ מאוזן אלא אם בעץ צומת אחת בלבד והיא השורש.
• ההפרש בין הגובה של שני תתי-עצים של אותו הצומת לעולם אינו גדול מאחד.
• אם $n=2^{h}$ אז העץ הוא עץ שלם.

ראו גם

• עץ חיפוש
• עץ אדום שחור
• עץ AVL

קישורים חיצוניים

מדיה וקבצים בנושא עץ מאוזן בוויקישיתוף