משתמש:RaHelR/טיוטה
 |
דף זה אינו ערך אנציקלופדי
| |
| דף זה אינו ערך אנציקלופדי | |
בסטטיסטיקה, השכיח הוא הערך שמופיע בתדירות הגבוהה ביותר בקבוצה של נתונים. במילים אחרות, זהו הערך שלו הסיכוי הטוב ביותר להיות זה שנדגם.
כמו הממוצע והחציון, השכיח הוא דרך להביע מידע חשוב על משתנה מקרי או אוכלוסייה באמצעות מספר בודד. ערכו של השכיח בהתפלגות נורמלית שווה לממוצע ולחציון, אך יכול להיות שונה מהם מאוד ב התפלגות א-סימטרית. יתרונו המשמעותי של השכיח על שאר מדדי המרכז היא תקפותו גם למשתנה בעל ערכים שמיים.
השכיח אינו בהכרח ערך יחיד, כיון שפונקציית צפיפות ההסתברות יכולה להיות בעלת מספר נקודות מקסימום- כלומר יכולים להיות מספר ערכים שלהם שכיחות זהה, שהיא המקסימלית. במקרה כזה, יהיו כל הערכים בעלי שכיחות זו השכיחים. המקרה הקיצוני ביותר מתרחש בהתפלגויות אחידות, שבהן כל הערכים שכיחים באותה מידה. בהתפלגויות סימטריות, כמו ההתפלגות הנורמלית, החציון, השכיח והממוצע (אם הוגדר) מתלכדים. עבור דגימות, אם ידוע שהן מפוזרות בהתפלגות סימטרית, ממוצע המדגם יכול לשמש כאומדן של השכיח.במרבית ההתפלגויות הסימטריות (כמו ההתפלגות הנורמלית), השכיח שווה בערכו לממוצע ולחציון.
חישוב השכיח
[עריכת קוד מקור | עריכה]במדגם בדיד
[עריכת קוד מקור | עריכה]השכיח של מדגם הוא הערך המופיע בו בתדירות הגבוהה ביותר. לדוגמא, השכיח של המדגם [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] הוא 6.לעומת זאת, ברשימת הנתונים [1, 1, 2, 4, 4] השכיח אינו ייחודי - קיימים שני ערכים בעלי אותה שכיחות, שהיא הגבוהה ביותר במדגם. ניתן לומר שההתפלגות היא דו- שיאית, בעוד קבוצה עם יותר משני שכיחים יכולה להיות מתוארת כרב- שיאית.
במדגם רציף
[עריכת קוד מקור | עריכה]המדגם הוא התפלגות רציפה, כגון [... .935, 1.211 ..., 2.430 ..., 3.668 ..., 3.874 ...], המושג הוא בלתי שימושי בצורתו הגולמית, שכן אין בו שני ערכים זהים, ולכן כל ערך יופיע בדיוק פעם אחת. על מנת להעריך את השכיח, מקובל לסדר את הנתונים במחלקות שוות רוחב, כמו להכנת היסטוגרמה, ולחשב את שכיחותה של כל מחלקה. מוצאים בקלות את המחלקה השכיחה- המחלקה שבה ההיסטוגרמה מגיעה לשיא- ואמצע מחלקה זו הוא השכיח. החיסרון בכך הוא שבדגימות קטנות או בינוניות, עלולה להיווצר הטיה בהתאם לרוחב המחלקה. דרך אחרת לחישוב השכיח במקרה כזה היא למצוא את נקודת המקסימום של פונקצית צפיפות ההסתברות.
הצגה גרפית
[עריכת קוד מקור | עריכה]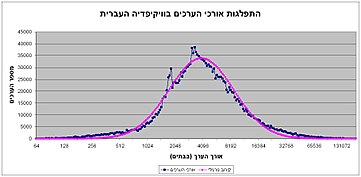
בסדרת ערכים, השכיח מוגדר כאמור על ידי ספירת ההופעות של הערכים השונים, אך דרך זו אינה נוחה. קיימות מספר דרכים להצגה גרפית של השכיח. מדגם בדיד יסודר לרוב בעמודות לפי ערכים, כמו בדיאגרמת מקלות או בהיסטוגרמה. בהצגה כזו, ניתן לאתר את השכיח בקלות: הערך השכיח הוא זה שהעמודה המיצגת אותו היא הגבוהה ביותר- בעל הצפיפות הגבוהה ביותר. בהיסטוגרמה, השכיח הוא אמצע המחלקה השכיחה ביותר. במדגם רציף, שבו ניתן להציג את ההתפלגות בקו אחד, ניתן לאתר את השכיח בגרף ע"י מציאת נק' המקסימום שלו.
השוואה למדדי מרכז אחרים
[עריכת קוד מקור | עריכה] ערך מורחב – מדד מיקום
ערך מורחב – מדד מיקום
הטבלה ממחישה היטב את ההבדלים בין שלושת מדדי המיקום המרכזיים:
| סוג | תיאור | דוגמא | תוצאה |
|---|---|---|---|
| ממוצע חשבוני | סכום ערכי המדגם מחולק במספרם\ | 7/(1+2+2+3+4+7+9) | 4 |
| חציון | הערך האמצעי בסידור עולה של הערכים | 1,2,2,3,4,7,9 | 3 |
| שכיח | הערך הנפוץ ביותר במדגם | 1,2,2,3,4,7,9 | 2 |
בניגוד לממוצע ולחציון, המושג "שכיח" הגיוני וישים גם על ערכים שמיים. למשל, אם המדגם הוא של שמות משפחה בישראל, והשם "כהן" מופיע הכי הרבה פעמים- השכיח יהיה "כהן". מובן שבדגימה כזו לא ניתן לחשב ממוצע או חציון. במערכת בחירות שבה המנצח נקבע על פי הרוב, המנצח הוא השכיח- בעוד שני שכיחים ומעלה ידרשו תהליך שובר שויון.
בניגוד לחציון, שהגיוני רק כאשר יש סדר ליניארי בין הערכים האפשריים, השכיח אינו דורש זאת- בכל מדגם יש משמעות למושג זה.
פונקצית ההפסד
[עריכת קוד מקור | עריכה]השכיח של מדגם מוגדר כערך שמספר הערכים השונים ממנו הוא הקטן ביותר. במילים אחרות, השכיח הוא הממזער של פונקציית ההפסד הבאה:
כאשר .



