משתמש:E QFish/למידת מכונה קוונטית
למידת מכונה קוונטית היא שילוב של אלגוריתמים קוונטיים בתוך תוכניות למידת מכונה .[1][2][3][4][5][6][7][8]
השימוש הנפוץ ביותר במונח מתייחס לאלגוריתמים של למידת מכונה לניתוח נתונים קלאסיים המבוצעים במחשב קוונטי, כלומר למידת מכונה משופרת קוונטית.[9][10][11] בעוד אלגוריתמים של למידת מכונה משמשים לחישוב כמויות עצומות של נתונים, למידת מכונה קוונטית משתמשת בקיוביטים ופעולות קוונטיות או במערכות קוונטיות מיוחדות כדי לשפר את מהירות החישוב ואת אחסון הנתונים שנעשו על ידי אלגוריתמים בתוכנית. [12] זה כולל שיטות היברידיות הכוללות עיבוד קלאסי וקוונטי כאחד, שבהן תתי שגרות קשות מבחינה חישובית מועברות למכשיר קוונטי חיצוני.[13][14][15] שגרות אלו יכולות להיות מורכבות יותר בטבען ולהתבצע מהר יותר במחשב קוונטי.[7] יתר על כן, ניתן להשתמש באלגוריתמים קוונטיים לניתוח מצבים קוונטיים במקום נתונים קלאסיים.[16][17]
מעבר למחשוב קוונטי, המונח "למידת מכונה קוונטית" קשור גם לשיטות למידת מכונה קלאסיות המיושמות על נתונים שנוצרו מניסויים קוונטיים (כלומר למידת מכונה של מערכות קוונטיות), כגון לימוד מעברי הפאזה של מערכת קוונטית[18][19] או יצירת ניסויים קוונטיים חדשים.[20][21][22]
למידת מכונה קוונטית מתרחבת גם אל ענף מחקר הבוחן קווי דמיון מתודולוגיים ומבניים בין מערכות פיזיות מסוימות ומערכות למידה, בפרט רשתות עצביות. לדוגמה, כמה טכניקות מתמטיות ומספריות מהפיזיקה הקוונטית ישימות ללמידה עמוקה קלאסית ולהיפך.[23][24][25]
יתר על כך, חוקרים חוקרים מושגים מופשטים יותר של תורת הלמידה ביחס למידע קוונטי, המכונה לעתים "תורת הלמידה הקוונטית".[26][27]
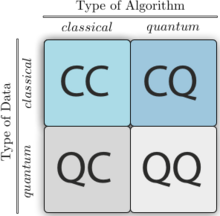
למידת מכונה עם מחשבים קוונטיים
[עריכת קוד מקור | עריכה]למידת מכונה משופרת קוונטית מתייחסת לאלגוריתמים קוונטיים שפותרים מטלות בלמידת מכונה, ובכך משפרים ולעיתים קרובות מזרזים טכניקות למידת מכונה קלאסיות. אלגוריתמים אלו דורשים בדרך כלל לקודד את אוסף הנתונים הקלאסי הנתון לתוך מחשב קוונטי כדי להפוך אותו לנגיש לעיבוד מידע קוונטי. לאחר מכן, מיושמות שגרות עיבוד מידע קוונטי והתוצאה של החישוב הקוונטי נקראת על ידי מדידת המערכת הקוונטית. לדוגמה, תוצאת המדידה של קיוביט חושפת את התוצאה של פעולת סיווג דו-ערכי. בעוד שהצעות רבות של אלגוריתמי למידת מכונת קוונטית הן עדיין תיאורטיות בלבד ודורשות בדיקה של מחשב קוונטי אוניברסלי בקנה מידה מלא, אחרות יושמו במכשירים קוונטיים בקנה מידה קטן או למטרות מיוחדות.
זיכרונות אסוציאטיביים קוונטיים וזיהוי תבניות קוונטיות
[עריכת קוד מקור | עריכה]זיכרונות אסוציאטיביים (או סמוכים) מסוגלים לזהות תוכן מאוחסן על בסיס דומי, במקום כתובות קבועות, כמו בזיכרונות גישה אקראית. ככאלה הם חייבים להיות מסוגלים לאחזר גם דפוסים לא שלמים וגם דפוסים פגומים, משימת למידת המכונה החיונית של זיהוי דפוסים.
זיכרונות אסוציאטיביים קלאסיים אופייניים מאחסנים דפוסי p ב- אינטראקציות (סינפסות) של מטריצת אנרגיה אמיתית וסימטרית על גבי רשת של n נוירונים מלאכותיים. הקידוד הוא כזה שהתבניות הרצויות הן מינימום מקומי של האנרגיה הפונקציונלית והשליפה מתבצעת על ידי צמצום האנרגיה הכוללת, החל מתצורה ראשונית.
למרבה הצער, זיכרונות אסוציאטיביים קלאסיים מוגבלים מאוד על ידי תופעת ההצלבה. כאשר מאוחסנים יותר מדי דפוסים, מופיעים זיכרונות מזויפים שמתרבים במהירות, כך שהנוף האנרגטי הופך לא מסודר ושליפה אינה אפשרית. מספר הדפוסים שניתן לאחסן מוגבל בדרך כלל על ידי פונקציה לינארית של מספר הנוירונים, .
זיכרונות אסוציאטיביים קוונטיים[2][3][4] (במימושם הפשוט ביותר) מאחסנים תבניות במטריצה אוניטרית U הפועלת על מרחב הילברט של n קיוביטים. השליפה מתממשת על ידי אבולוציה יחידתית של מצב התחלתי קבוע לסופרפוזיציה קוונטית של הדפוסים הרצויים עם התפלגות הסתברות בשיאה בדפוס הדומה ביותר לקלט. מעצם טבעו הקוונטי מאוד, תהליך השליפה הוא לפיכך הסתברותי. כיוון שזיכרונות אסוציאטיביים קוונטיים חופשיים מהצלבה, למרות זאת, זיכרונות מזויפים לעולם אינם נוצרים. בהתאם, יש להם קיבולת עדיפה על אלה הקלאסיים. מספר הפרמטרים במטריצה האוניטרית U הוא . כך ניתן לקבל זיכרונות קוונטיים אסוציאטיביים יעילים, נטולי זיכרון מזויף עבור כל מספר פולינומי של תבניות.
הדמיית אלגברה לינארית עם אמפליטודות קוונטיות
[עריכת קוד מקור | עריכה]מספר אלגוריתמים קוונטיים ללמידת מכונה מבוססים על הרעיון של קידוד משרעת, כלומר לשייך את המשרעות של מצב קוונטי לקלט ופלט של חישובים.[30][31][32] מאז מצב של קיוביטים מתואר על ידי אמפליטודות מורכבות, קידוד מידע זה יכול לאפשר ייצוג קומפקטי אקספוננציאלי. באופן אינטואיטיבי, זה מתאים לשיוך התפלגות הסתברות בדיד על משתנים אקראיים בינאריים עם וקטור קלאסי. המטרה של אלגוריתמים המבוססים על קידוד משרעת היא לנסח אלגוריתמים קוונטיים שהמשאבים שלהם גדלים בצורה פולינומית במספר הקיוביטים , המסתכמת במורכבות זמן לוגריתמית במספר האמפליטודות ובכך בממד הקלט.
אלגוריתמים רבים של למידת מכונות קוונטיות בקטגוריה זו מבוססים על וריאציות של האלגוריתם הקוונטי עבור מערכות משוואות ליניאריות [33] (הנקרא עממית HHL, על שם מחברי המאמר) אשר, בתנאים ספציפיים, מבצע היפוך מטריצה תוך שימוש בכמות משאבים פיזיים אשר גדל רק לוגריתמית במידות המטריצה. אחד התנאים הללו הוא שניתן לדמות ביעילות המילטוניאן שמתאים מבחינת הכניסה למטריצה, מה שכידוע אפשרי אם המטריצה דלילה או בעלת דרגה נמוכה. [34] לשם התייחסות, כל אלגוריתם קלאסי מוכר להיפוך מטריצה דורש מספר פעולות שגדלות יותר מברביעית בממד המטריצה (למשל ), אך הם אינם מוגבלים למטריצות דלילות.
ניתן ליישם היפוך מטריצה קוונטית על שיטות למידת מכונה שבהן האימון מצטמצם לפתרון מערכת משוואות ליניארית, למשל ברגרסיה לינארית של ריבועים קטנים, [31] [32] גרסת הריבועים הקטנים ביותר של תמיכה במכונות וקטוריות, [30] ותהליכי גאוס. [35]
צוואר בקבוק מכריע של שיטות המדמות חישובי אלגברה ליניאריים עם אמפליטודות של מצבים קוונטיים הוא הכנת מצבים, שלעיתים קרובות דורשת לאתחל מערכת קוונטית במצב שהמשרעות שלו משקפות את התכונות של מערך הנתונים כולו. למרות ששיטות יעילות להכנת המצב ידועות למקרים ספציפיים, [36] [37] שלב זה מסתיר בקלות את מורכבות המשימה. [38] [39]
אלגוריתמים קוונטיים וריאציוניים (אק"רים)
[עריכת קוד מקור | עריכה]אק"רים הם אחד האלגוריתמים הקוונטיים הנחקרים ביותר שכן החוקרים מצפים שכל היישומים הדרושים למחשב הקוונטי ישתמשו באק"רים וגם אק"רים ממלאים את הציפייה להשגת עליונות קוונטית. אק"רים היא גישה קוונטית-קלאסית מעורבת שבה המעבד הקוונטי מכין מצבים קוונטיים והמדידה מתבצעת והאופטימיזציה נעשית על ידי מחשב קלאסי. אק"רים נחשבים הטובים ביותר עבור NISQ מכיוון שאק"רים עמידים לרעש בהשוואה לאלגוריתמים אחרים ומעניקים עליונות קוונטית עם כמה מאות קיוביטים בלבד. חוקרים חקרו אלגוריתמים מבוססי מעגלים כדי לפתור בעיות אופטימיזציה ולמצוא את אנרגיית מצב הקרקע של מערכות מורכבות, שהיו קשות לפתרון או שנדרשו זמן רב כדי לבצע את החישוב באמצעות מחשב קלאסי. [40] [41]
מעגלים קוונטיים וריאציוניים (מק"וים)
[עריכת קוד מקור | עריכה]מעגלים קוונטיים וריאציוניים הידועים גם בשם מעגלים קוונטיים פרמטרים (מק"פים) מבוססים על אלגוריתמים קוונטיים וריאציוניים (אק"רים). מק"וים מורכבים משלושה חלקים: הכנת מצבים ראשוניים, מעגל קוונטי ומדידה. חוקרים חוקרים בהרחבה מק"וים, שכן הם משתמשים בכוחו של חישוב קוונטי כדי ללמוד תוך זמן קצר וגם משתמשים בפחות פרמטרים מאשר מקבילם הקלאסיים. הוכח תיאורטית ומספרית שאנו יכולים להעריך פונקציות לא-לינאריות, כמו אלו המשמשות ברשתות עצביות, בתוך מעגלים קוונטיים. בשל עליונות המק"וים, הרשת העצבית הוחלפה ב-מק"וים במשימות למידת חיזוק ובאלגוריתמים גנרטיביים. האופי המהותי של התקנים קוונטיים לקראת דה-קוהרנטיות, שגיאות שער אקראיות ושגיאות מדידה גרמו לפוטנציאל גבוה להגביל את האימון של מעגלי הווריאציה. אימון ה-מק"וים על המכשירים הקלאסיים לפני השימוש בהם על מכשירים קוונטיים עוזר להתגבר על בעיית רעש הדה-קוהרנטיות שהגיע ממספר החזרות לאימון. [42] [43]
מסווג בינארי קוונטי
[עריכת קוד מקור | עריכה]ארגון מחדש של דפוסים הוא אחת המשימות החשובות של למידת מכונה, סיווג בינארי הוא אחד הכלים או האלגוריתמים למציאת דפוסים. סיווג בינארי משמש בלמידה מפוקחת ובלמידה ללא פיקוח. בלמידת מכונה קוונטית, ביטים קלאסיים מומרים לקיוביטים והם ממופים למרחב הילברט; נתוני ערכים מורכבים משמשים במסווג בינארי קוונטי כדי להשתמש ביתרון של מרחב הילברט. [44] [45] על ידי ניצול תכונות מכניקת הקוונטים כגון סופרפוזיציה, קשירה, הפרעות, המסווג הבינארי הקוונטי מייצר את התוצאה המדויקת בפרק זמן קצר. [46]
אלגוריתמים של למידת מכונה קוונטית המבוססים על חיפוש גרובר
[עריכת קוד מקור | עריכה]גישה נוספת לשיפור למידת מכונה קלאסית עם עיבוד מידע קוונטי משתמשת בשיטות הגברת משרעת המבוססות על אלגוריתם החיפוש של גרובר, אשר הוכח כפותר בעיות חיפוש לא מובנות עם האצה ברביעית בהשוואה לאלגוריתמים קלאסיים. ניתן להשתמש בשגרות קוונטיות אלה ללימוד אלגוריתמים המתורגמים למשימת חיפוש לא מובנית, כפי שניתן לעשות, למשל, במקרה של ה- k-medians [47] והאלגוריתמים של השכנים k-הסמוכים ביותר . [9] יישומים אחרים כוללים האצה ברביעית באימון פרצפטרון וחישוב הקשב .
דוגמה להגברת משרעת בשימוש באלגוריתם למידת מכונה היא מזעור אלגוריתם החיפוש של גרובר. שבו תת שגרה משתמשת באלגוריתם החיפוש של גרובר כדי למצוא אלמנט פחות מאלמנט שהוגדר קודם לכן. זה יכול להיעשות עם אורקל שקובע אם מצב עם אלמנט מתאים קטן מהמצב שהוגדר מראש. האלגוריתם של גרובר יכול אז למצוא אלמנט כך שהתנאי שלנו יתקיים. המינימום מאותחל על ידי אלמנט אקראי כלשהו במערך הנתונים שלנו, ובאופן איטרטיבי מבצע את תת-השגרה הזו כדי למצוא את האלמנט המינימלי במערך הנתונים. מזעור זה משמש בעיקר ב-k-medians קוונטיים, ויש לו האצה בלפחות בהשוואה לגרסאות קלאסיות של k-medians, ש הוא מספר נקודות הנתונים ו הוא מספר האשכולות. [47]
הגברה משרעת משולבת לעתים קרובות עם הליכות קוונטיות כדי להשיג את אותה האצה ברביעית. הליכות קוונטיות הוצעו כדי לשפר את אלגוריתם ה-PageRank של גוגל [48] וכן את הביצועים של סוכני למידת חיזוק במסגרת הסימולציה השלכתית. [49]
למידת חיזוק קוונטי
[עריכת קוד מקור | עריכה]למידת חיזוק היא ענף של למידת מכונה נבדלת מלמידה מפוקחת ובלתי מפוקחת, אשר מודה גם בשיפורים קוונטיים. [50] [49] בלימוד חיזוק משופר-קוונטית, סוכן קוונטי מקיים אינטראקציה עם סביבה קלאסית או קוונטית ומדי פעם מקבל תגמולים על פעולותיו, מה שמאפשר לסוכן להתאים את התנהגותו - במילים אחרות, ללמוד מה לעשות כדי לזכות בתגמולים נוספים. במצבים מסוימים, בין אם בגלל יכולת העיבוד הקוונטי של הסוכן, [49] או בשל האפשרות לחקור את הסביבה בסופרפוזיציות, [29] עשויה להיות מושגת האצה קוונטית. יישום של סוגים אלה של פרוטוקולים הוצעו עבור מערכות של יונים לכודים [51] ומעגלים מוליכים-על . [52] האצה קוונטית של זמן קבלת ההחלטות הפנימי של הסוכן [49] הוכחה בניסוי ביונים לכודים, [53] בעוד שהאצה קוונטית של זמן הלמידה באינטראקציה קוהרנטית לחלוטין ('קוונטית') בין סוכן לסביבה התממשה בניסוי במערך פוטוני. [54]
חישול קוונטי
[עריכת קוד מקור | עריכה]
שגיאות פרמטריות בתבנית:הפניה לערך מורחב
פרמטרים ריקים [ 2 ] לא מופיעים בהגדרת התבנית
חישול קוונטי הוא טכניקת אופטימיזציה המשמשת לקביעת המינימום והמקסימום המקומיים של פונקציה על פני קבוצה נתונה של פונקציות מועמדות. זוהי שיטה של דיסקרטיזציה של פונקציה עם מינימום או מקסימום מקומיים רבים על מנת לקבוע את הנצפים של הפונקציה. ניתן להבחין בין התהליך לבין חישול מדומה על ידי תהליך המנהור קוונטי, שבאמצעותו חלקיקים עוברים דרך מחסומים קינטיים או פוטנציאליים ממצב גבוה למצב נמוך. חישול קוונטי מתחיל מסופרפוזיציה של כל המצבים האפשריים של מערכת, במשקל שווה. אז משוואת שרדינגר התלויה בזמן מנחה את התפתחות הזמן של המערכת, ומשמשת להשפיע על המשרעת של כל מצב ככל שהזמן גדל. בסופו של דבר, ניתן להגיע למצב הקרקע כדי להניב את המילטוניאן המיידי של המערכת.
NISQ Circuit כדגם קוונטי
[עריכת קוד מקור | עריכה]ככל שעומק המעגל הקוונטי מתקדם במכשירי NISQ, רמת הרעש עולה, מה שמציב אתגר משמעותי בחישוב מדויק של עלויות ושיפועים בדגמי אימון. סבילות הרעש תשתפר על ידי שימוש בקולטן הקוונטי ובאלגוריתם הקוונטי בחומרה הקוונטית הנגישה כעת.
חיבור קבוע של רכיבים דומים המכונים נוירונים מהווה את הבסיס אפילו לרשתות המוח המורכבות ביותר. בדרך כלל, לנוירון יש שתי פעולות: התוצר הפנימי ופונקציית הפעלה . בניגוד לפונקציית ההפעלה, שהיא בדרך כלל לא ליניארית, התוצר הפנימי הוא תהליך ליניארי. עם מחשוב קוונטי, תהליכים ליניאריים עשויים להתבצע בקלות בנוסף, בשל פשטות היישום, פונקציית הסף מועדפת על ידי רוב הנוירונים הקוונטיים עבור פונקציות הפעלה.
שגיאות פרמטריות בתבנית:מקור
שימוש בפרמטרים מיושנים [ תאריך ] [דרוש מקור]</link>[ <span title="This claim needs references to reliable sources. (January 2023)">צריך ציטוט</span> ]
טכניקות דגימה קוונטית
[עריכת קוד מקור | עריכה]דגימה מהתפלגות הסתברות בממדים גבוהים היא הליבה של ספקטרום רחב של טכניקות חישוביות עם יישומים חשובים במדע, הנדסה וחברה. דוגמאות כוללות למידה עמוקה, תכנות הסתברותי ויישומי למידת מכונה ובינה מלאכותית אחרים.
בעיה קשה מבחינה חישובית, שהיא המפתח עבור כמה משימות למידת מכונה רלוונטיות, היא הערכת ממוצעים על פני מודלים הסתברותיים המוגדרים במונחים של התפלגות בולצמן . הדגימה ממודלים הסתברותיים גנריים היא קשה: אלגוריתמים המסתמכים במידה רבה על דגימה צפויים להישאר בלתי ניתנים לפתרון, לא משנה כמה גדולים וחזקים יהיו משאבי מחשוב קלאסיים. אף על פי שמחשלים קוונטיים, כמו אלה המיוצרים על ידי D-Wave Systems, תוכננו לבעיות אופטימיזציה קומבינטורית מאתגרות, הם הוכרו לאחרונה כמועמד פוטנציאלי להאיץ חישובים המסתמכים על דגימה על ידי ניצול השפעות קוונטיות. [55]
כמה קבוצות מחקר חקרו לאחרונה את השימוש בחומרת חישול קוונטית לאימון מכונות בולצמן ורשתות עצביות עמוקות . [56] [57] [58] הגישה הסטנדרטית לאימון מכונות בולצמן מסתמכת על חישוב של ממוצעים מסוימים שניתן להעריך על ידי טכניקות דגימה סטנדרטיות, כגון אלגוריתמים של שרשרת מרקוב מונטה קרלו . אפשרות נוספת היא להסתמך על תהליך פיזיקלי, כמו חישול קוונטי, שיוצר באופן טבעי דגימות מהתפלגות בולצמן. המטרה היא למצוא את פרמטרי הבקרה האופטימליים המייצגים בצורה הטובה ביותר את ההתפלגות האמפיריאלית של אוסף נתונים נתון.
מערכת ה-D-Wave 2X המתארחת במרכז המחקר איימס של נאס"א שימשה לאחרונה ללמידה של סוג מיוחד של מכונות בולצמן מוגבלות שיכולות לשמש אבן בניין לארכיטקטורות למידה עמוקה. [57] עבודה משלימה שהופיעה בערך בו-זמנית הראתה שניתן להשתמש בחישול קוונטי ללמידה מפוקחת במשימות סיווג. אותו מכשיר שימש מאוחר יותר לאימון מכונת בולצמן המחוברת במלואה ליצור, לשחזר ולסווג ספרות בכתב יד מוקטנות ברזולוציה נמוכה, בין אוספי נתונים סינתטיים אחרים. [59] בשני המקרים, למודלים שאומנו על ידי חישול קוונטי היו ביצועים דומים או טובים יותר מבחינת איכות. השאלה האולטימטיבית שמניעה את המאמץ הזה היא האם יש האצה קוונטית ביישומי דגימה. ניסיון בשימוש במחשלים קוונטיים לאופטימיזציה קומבינטורית מצביע על כך שהתשובה אינה פשוטה. נעשה שימוש גם בחישול הפוך כדי לפתור מכונת בולצמן מוגבלת קוונטית מחוברת לחלוטין. [60]
בהשראת ההצלחה של מכונות בולצמן המבוססות על הפצת בולצמן הקלאסית, הוצעה לאחרונה גישת למידת מכונה חדשה המבוססת על התפלגות בולצמן קוונטית של שדה רוחבי של איזינג המילטוניאן. [61] בשל האופי הלא-קומוטטיבי של מכניקת הקוונטים, תהליך האימון של מכונת בולצמן הקוונטית יכול להפוך ללא טריוויאלי. בעיה זו נעקפה, במידה מסוימת, על ידי הכנסת גבולות להסתברויות הקוונטיות, מה שמאפשר למחברים לאמן את המודל ביעילות על ידי דגימה. ייתכן שסוג מסוים של מכונת בולצמן קוונטית הוכשר ב-D-Wave 2X באמצעות כלל למידה מקביל לזה של מכונות בולצמן קלאסיות. [59] [62]
חישול קוונטי אינו הטכנולוגיה היחידה לדגימה. בתרחיש של הכנה ומדידה, מחשב קוונטי אוניברסלי מכין מצב תרמי, שנדגם לאחר מכן על ידי מדידות. זה יכול להפחית את הזמן הנדרש לאימון מכונת בולצמן מוגבלת עמוקה, ולספק מסגרת עשירה ומקיפה יותר ללמידה עמוקה מאשר מחשוב קלאסי. אותן שיטות קוונטיות מאפשרות גם הכשרה יעילה של מכונות בולצמן מלאות ודגמים רב-שכבתיים המחוברים לחלוטין ואין להן מקבילות קלאסיות ידועות. בהסתמכות על פרוטוקול הכנת מצב תרמי יעיל המתחיל ממצב שרירותי, רשתות מרקוב לוגיות משופרות מנצלות את הסימטריות ואת מבנה המקומיות של המודל הגרפי ההסתברותי שנוצר על ידי תבנית לוגיקה מסדר ראשון . [63] [19] זה מספק הפחתה אקספוננציאלית במורכבות החישובית בהסקה הסתברותית, ובעוד שהפרוטוקול מסתמך על מחשב קוונטי אוניברסלי, תחת הנחות מתונות ניתן להטמיע אותו על חומרת חישול קוונטי עכשווית.
רשתות עצביות קוונטיות
[עריכת קוד מקור | עריכה]אנלוגים קוונטיים או הכללות של רשתות עצביות קלאסיות מכונות לעתים קרובות רשתות עצביות קוונטיות . המונח נתבע על ידי מגוון רחב של גישות, כולל הטמעה והרחבה של רשתות עצביות באמצעות פוטונים, מעגלים וריאציים שכבתיים או מודלים קוונטיים מסוג איזינג. רשתות עצביות קוונטיות מוגדרות לעתים קרובות כהרחבה על המודל של דויטש של רשת חישובית קוונטית. [64] בתוך המודל הזה, שערים לא ליניאריים ובלתי הפיכים, שאינם דומים לאופרטור ההמילטוניאן, נפרסים כדי לשער את אוסף הנתונים הנתון. [64] שערים כאלה גורמים לכך שלא ניתן לצפות בפאזות מסוימות ומייצרים תנודות ספציפיות. [64] רשתות עצביות קוונטיות מיישמות את המידע הקוונטי והחישוב הקוונטי העיקרי למחשוב נוירו-מחשוב קלאסי. [65] מחקר עדכני מראה ש-רע"ק יכול להגדיל באופן אקספוננציאלי את כמות כוח המחשוב ואת דרגות החופש של מחשב, המוגבלת עבור מחשב קלאסי לגודלו. [65] לרשת עצבית קוונטית יש יכולות חישוביות להקטין את מספר הצעדים, הקיוביטים בשימוש וזמן החישוב. [64] פונקציית הגל של מכניקת הקוונטים היא הנוירון לרשתות עצביות. כדי לבדוק יישומים קוונטיים ברשת עצבית, מולקולות נקודה קוונטיות מופקדות על מצע של GaAs או דומה כדי לתעד כיצד הן מתקשרות זו עם זו. ניתן להתייחס לכל נקודה קוונטית כאי של פעילות חשמלית, וכאשר נקודות כאלה קרובות מספיק (בערך 10 - 20 ננומטר) [66] אלקטרונים יכולים לעבור במנהרה מתחת לאיים. חלוקה שווה על פני המצע בסטים של שניים יוצרת דיפולים ובסופו של דבר שני מצבי ספין, למעלה או למטה. מצבים אלה ידועים בדרך כלל כקיוביטים עם מצבים מתאימים של ו בסימון דיראק. [66]
רשת קונבולוציונית קוונטית
[עריכת קוד מקור | עריכה]תכנון חדש לוקטורים רב מימדיים המשתמש במעגלים כמסנני קונבולוציה [67] הוא רק"ק. זה נוצר בהשראת היתרונות של ר"קים [68] [69] ומהכוח של למ"ק. זה נעשה באמצעות שילוב של מעגל קוונטי וריאצי (מק"ו) [70] ורשת עצבית עמוקה [71] (רע"ע), תוך ניצול מלא של הכוח של עיבוד מקביל במיוחד על סופרפוזיציה של מצב קוונטי עם מספר סופי של קיוביטים . האסטרטגיה העיקרית היא ביצוע תהליך אופטימיזציה איטרטיבי במכשירי NISQ [72] ללא ההשפעה השלילית של רעש, שאולי משולב בפרמטר המעגל, וללא צורך בתיקון שגיאות קוונטי. [73]
המעגל הקוונטי חייב לטפל ביעילות במידע מרחבי על מנת ש-רק"ק יתפקד כ-ר"ק. מסנן הקונבולציה הוא הטכניקה הבסיסית ביותר לשימוש במידע מרחבי. מסנן קונבולוציוני קוונטי אחד או יותר מרכיבים רשת עצבית קוונטית (רק"ק), וכל אחד מהמסננים הללו הופך נתוני קלט באמצעות מעגל קוונטי שניתן ליצור בצורה מאורגנת או אקראית. שלושה חלקים המרכיבים את המסנן הקונבולוציוני הקוונטי הם: המקודד, המעגל הקוונטי בעל הפרמטרים (מק"פ), [74] והמדידה. ניתן לראות במסנן הקונבולוציוני הקוונטי הרחבה של המסנן ב-ר"ק המסורתי מכיוון שהוא תוכנן עם פרמטרים הניתנים לאימון.
רשתות נוירונים קוונטיות מנצלות את המבנים ההיררכיים, [75] ולכל שכבה שלאחר מכן, מספר הקיוביטים מהשכבה הקודמת מצטמצם בפקטור של שניים. עבור n קיוביטי קלט, למבנים אלה יש O(log(n)) שכבות, המאפשרות עומק מעגל רדוד. בנוסף, הם מסוגלים להימנע מ"רמה עקרה", אחת הבעיות המשמעותיות ביותר באלגוריתמים מבוססי מק"פ, מה שמבטיח יכולת אימון. [76] למרות העובדה שמודל רק"ק אינו כולל את הפעולה הקוונטית המקבילה, הרעיון הבסיסי של שכבת האיגום מוצע גם כדי להבטיח תוקף. בארכיטקטורת רק"ק, שכבת הבריכה ממוקמת בדרך כלל בין שכבות קונבולוציוניות עוקבות. תפקידו הוא לכווץ את הגודל המרחבי של הייצוג תוך שמירה על תכונות חיוניות, מה שמאפשר לו לצמצם את מספר הפרמטרים, לייעל את מחשוב הרשת ולנהל התאמת יתר. תהליך כזה יכול להתבצע תוך שימוש בטומוגרפיה מלאה על המצב כדי לצמצם אותו עד לקיוביט אחד ואז לעבד אותו בסאב ווי. סוג היחידה הנפוץ ביותר בשכבת הבריכה הוא max pooling, אם כי ישנם גם סוגים נוספים. בדומה לרשתות זרימה קדימה קונבנציונליות, המודול האחרון הוא שכבה מחוברת במלואה עם חיבורים מלאים לכל ההפעלה בשכבה הקודמת. איווריות תרגום, הדורשת בלוקים זהים של שערים קוונטיים עם פרמטרים בתוך שכבה, היא תכונה ייחודית של ארכיטקטורת רק"ק. [77]
רשת עצבית קוונטית דיסיפטיבית
[עריכת קוד מקור | עריכה]רע"קים דיסיפטיבים (רעק"דים) בנויים משכבות של קיוביטים המשולבים על ידי פרספטרון הנקראות אבני בניין, בעלות עיצוב יוניטרי שרירותי. כל צומת בשכבת הרשת של רעק"ד מקבל אוסף מובהק של קיוביטים, ולכל קיוביט ניתן גם פרספטרון קוונטי יוניטרי ייחודי לאפיין אותו. [78] מידע על מצבי הקלט מועבר דרך הרשת בשיטת זרימה קדימה, מיפוי מעבר שכבה לשכבה על הקיוביטים של שתי השכבות הסמוכות, כפי שהשם מרמז. מונח דיסיפטיבי מתייחס גם לעובדה ששכבת הפלט נוצרת על ידי הקיוביטים הנלווים בזמן ששכבות הקלט נשמטות תוך מעקב אחר השכבה הסופית. [79] בעת ביצוע משימת למידה מפוקחת רחבה, משתמשים ב-רעק"ד ללימוד מטריצה יוניטרית המחברת את מצבי הקלט והפלט הקוונטים. נתוני האימון עבור משימה זו מורכבים מהמצב הקוונטי ומהתוויות הקלאסיות המתאימות.
בהשראת הרשת האנדרסרית הקלאסית (GAN) הקלאסית המוצלחת ביותר, מוצגת רשת יריבות קוונטית מתפזרת (DQGAN) ללמידה ללא פיקוח של נתוני האימון ללא תווית. המחולל והמבדיל הם שני רעק"דs המרכיבים DQGAN יחיד. מטרתו של המחולל היא ליצור מצבי הכשרה כוזבים שהמבחנה אינו יכול להבדיל מאלה האמיתיים, בעוד שמטרתו של המפלה היא להפריד את מצבי האימון האמיתיים מהמצבים המזויפים שנוצרו על ידי המחולל. המאפיינים הרלוונטיים של אוסף ההדרכה נלמד על ידי המחולל על ידי הכשרה חלופית ויריבית של הרשתות המסייעות בייצור סטים המרחיבים את מערך ההדרכה. ל-DQGAN יש ארכיטקטורה קוונטית מלאה והוא מאומן בנתונים קוונטיים.
דגמי מרקוב קוונטים נסתרים
[עריכת קוד מקור | עריכה]מודלים של מרקוב קוונטיים [80] (HQMMs) הם גרסה משופרת קוונטית של מודלים סמויים של מרקוב (HMMs), המשמשים בדרך כלל למודל נתונים רציפים בתחומים שונים כמו רובוטיקה ועיבוד שפה טבעית . בניגוד לגישה של אלגוריתמים אחרים של למידת מכונה משופרת קוונטית, ניתן לראות ב-HQMM מודלים בהשראת מכניקת הקוונטים שניתן להפעיל גם במחשבים קלאסיים. [81] כאשר HMMs קלאסיים משתמשים בוקטורי הסתברות כדי לייצג מצבי 'אמונה' נסתרים, HQMMs משתמשים באנלוג הקוונטי: מטריצות צפיפות . עבודה אחרונה הראתה שניתן ללמוד בהצלחה מודלים אלה על ידי מיקסום סבירות היומן של הנתונים הנתונים באמצעות אופטימיזציה קלאסית, וישנן עדויות אמפיריות לכך שמודלים אלה יכולים לדגמן נתונים רציפים בצורה טובה יותר בהשוואה ל-HMMs קלאסיים בפועל, אם כי עבודה נוספת היא נדרש כדי לקבוע בדיוק מתי וכיצד מופקות ההטבות הללו. [81] בנוסף, מכיוון ש-HMMs קלאסי הם סוג מסוים של Bayes Net, היבט מרגש של HQMMs הוא שהטכניקות המשמשות מראות כיצד אנו יכולים לבצע הסקה בייסיאנית קוונטית-אנלוגית, מה שאמור לאפשר בנייה כללית של גרסאות קוונטיות של מודלים גרפיים הסתברותיים . [81]
למידה מלאה של מכונות קוונטיות
[עריכת קוד מקור | עריכה]במקרה הכללי ביותר של למידת מכונה קוונטית, גם מכשיר הלמידה וגם המערכת הנחקרת, כמו גם האינטראקציה ביניהם, הם קוונטיים לחלוטין. חלק זה נותן כמה דוגמאות לתוצאות בנושא זה.
מחלקה אחת של בעיה שיכולה להפיק תועלת מהגישה הקוונטית המלאה היא זו של 'למידה' של מצבים, תהליכים או מדידות קוונטיים לא ידועים, במובן זה שניתן לאחר מכן לשחזר אותם במערכת קוונטית אחרת. לדוגמה, ייתכן שתרצה ללמוד מדידה המבדילה בין שני מצבים קוהרנטיים, בהינתן לא תיאור קלאסי של המצבים שיש להפלות, אלא קבוצה של מערכות קוונטיות לדוגמה שהוכנו במצבים אלה. הגישה הנאיבית תהיה תחילה לחלץ תיאור קלאסי של המדינות ולאחר מכן ליישם מדידה אבחנה אידיאלית המבוססת על מידע זה. זה ידרוש רק למידה קלאסית. עם זאת, אפשר להראות שגישה קוונטית מלאה עדיפה בהחלט במקרה זה. [82] (זה מתייחס גם לעבודה על התאמת דפוסים קוונטיים. [83] ) ניתן לגשת לבעיה של למידה של טרנספורמציות יחידניות בצורה דומה. [84]
מעבר לבעיה הספציפית של למידה של מצבים וטרנספורמציות, משימת האשכול מאפשרת גם גרסה קוונטית מלאה, שבה הן האורקל שמחזיר את המרחק בין נקודות הנתונים והן מכשיר עיבוד המידע שמפעיל את האלגוריתם הם קוונטיים. [85] לבסוף, הוצגה מסגרת כללית המשתרעת על למידה מפוקחת, ללא פיקוח ולמידת חיזוק במסגרת הקוונטית המלאה, [29] שבה הוכח גם שהאפשרות לחטט בסביבה בסופרפוזיציות מאפשרת האצה קוונטית בלמידת חיזוק. האצה כזו בפרדיגמת החיזוק-למידה הוכחה בניסוי במערך פוטוני. [54]
למידת מכונה קוונטית ניתנת להסבר
[עריכת קוד מקור | עריכה]הצורך במודלים הניתנים להבנה על ידי בני אדם מופיע בלמידת מכונות קוונטיות באנלוגיה ללמידת מכונה קלאסית ומניע את תחום המחקר של למידת מכונות קוונטיות הניתנות להסבר (או XQML באנלוגיה ל- XAI/XML ). מאמצים אלה מכונים לעתים קרובות גם למידת מכונה לפירוש (IML, ובהרחבה IQML). [86] XQML/IQML יכול להיחשב ככיוון מחקר חלופי במקום מציאת יתרון קוונטי. [87] לדוגמה, נעשה שימוש ב-XQML בהקשר של זיהוי וסיווג תוכנות זדוניות לנייד. [88] ערכי Shapley קוונטיים הוצעו גם כדי לפרש שערים בתוך מעגל המבוסס על גישה תיאורטית של המשחק. [89] למטרה זו, שערים במקום תכונות פועלים כשחקנים במשחק קואליציוני עם פונקציית ערך התלויה במדידות של המעגל הקוונטי של עניין. בנוסף, הוצעה גם גרסה קוונטית של הטכניקה הקלאסית הידועה בשם LIME (הסברים ליניאריים ניתנים לפירוש מודל-אגנוסטי) [90] המכונה Q-LIME. [91]
למידה קלאסית מיושמת על בעיות קוונטיות
[עריכת קוד מקור | עריכה]המונח "למידת מכונה קוונטית" מתייחס לפעמים ללמידת מכונה קלאסית המבוצעת על נתונים ממערכות קוונטיות. דוגמה בסיסית לכך היא טומוגרפיה של מצב קוונטי, שבה לומדים מצב קוונטי ממדידה. יישומים אחרים כוללים לימוד המילטון [92] ויצירה אוטומטית של ניסויים קוונטיים. [20]
תורת הלמידה הקוונטית
[עריכת קוד מקור | עריכה]תורת הלמידה הקוונטית עוסקת בניתוח מתמטי של ההכללות הקוונטיות של מודלים למידה קלאסיים ושל ההאצות האפשריות או שיפורים אחרים שהם עשויים לספק. המסגרת דומה מאוד לזו של תורת הלמידה החישובית הקלאסית, אך הלומד במקרה זה הוא מכשיר לעיבוד מידע קוונטי, בעוד שהנתונים עשויים להיות קלאסיים או קוונטיים. יש להבדיל בין תיאוריית הלמידה הקוונטית לבין למידת המכונה המשופרת הקוונטית שנדונה לעיל, כאשר המטרה הייתה לשקול בעיות ספציפיות ולהשתמש בפרוטוקולים קוונטיים כדי לשפר את מורכבות הזמן של אלגוריתמים קלאסיים לבעיות אלו. למרות שתורת הלמידה הקוונטית עדיין בפיתוח, הושגו תוצאות חלקיות בכיוון זה. [93]
נקודת המוצא בתורת הלמידה היא בדרך כלל שיעור מושגים, קבוצה של מושגים אפשריים. בדרך כלל מושג הוא פונקציה בתחום כלשהו, כגון . לדוגמה, מחלקת המושגים יכולה להיות קבוצת נוסחאות הצורה הרגילה (DNF) על n סיביות או קבוצת המעגלים הבוליאניים בעלי עומק קבוע כלשהו. המטרה של הלומד היא ללמוד (בדיוק או בקירוב) מושג יעד לא ידוע משיעור מושג זה. ייתכן שהלומד מקיים אינטראקציה אקטיבית עם מושג היעד, או מקבל דגימות ממנו באופן פסיבי.
בלמידה פעילה, הלומד יכול לבצע שאילתות חברות למושג היעד c, ולבקש את הערך שלו c(x) בקלט x שנבחר על ידי הלומד. לאחר מכן על הלומד לשחזר את מושג היעד המדויק, בסבירות גבוהה. במודל של למידה מדויקת קוונטית, הלומד יכול לבצע שאילתות חברות בסופרפוזיציה קוונטית. אם המורכבות של הלומד נמדדת במספר שאילתות החברות שהוא מבצע, אז לומדים מדויקים בקוונטים יכולים להיות יעילים יותר באופן פולינומי מאשר לומדים קלאסיים עבור כמה משיעורי מושג, אבל לא יותר. [94] אם המורכבות נמדדת לפי כמות הזמן שהלומד משתמש, אז יש שיעורי מושג שניתן ללמוד ביעילות על ידי לומדים קוונטיים אך לא על ידי לומדים קלאסיים (תחת הנחות מורכבות-תיאורטיות סבירות). [94]
מודל טבעי של למידה פסיבית הוא הלמידה של Valiant כנראה בערך נכונה (PAC) . כאן הלומד מקבל דוגמאות אקראיות (x,c(x)), כאשר x מחולק לפי התפלגות לא ידועה כלשהי D. מטרתו של הלומד היא להוציא פונקציית השערה h כך ש-h(x)=c(x) בהסתברות גבוהה כאשר x מצויר לפי D. על הלומד להיות מסוגל לייצר ח 'נכון בקירוב' כזה עבור כל D וכל מושג יעד c במחלקת המושגים שלו. אנו יכולים לשקול להחליף את הדוגמאות האקראיות בדוגמאות קוונטיות פוטנציאליות חזקות יותר . במודל ה-PAC (והמודל האגנוסטי הקשור אליו), זה לא מפחית משמעותית את מספר הדוגמאות הדרושות: עבור כל מחלקה של מושג, מורכבות הדגימה הקלאסית והקוונטית זהה עד לגורמים קבועים. [95] עם זאת, עבור למידה תחת התפלגות קבועה D, דוגמאות קוונטיות יכולות להועיל מאוד, למשל ללימוד DNF תחת התפלגות אחידה. [96] כאשר בוחנים את מורכבות הזמן, קיימות כיתות מושגים שניתן ללמוד PAC ביעילות על ידי לומדים קוונטיים, אפילו מדוגמאות קלאסיות, אך לא על ידי לומדים קלאסיים (שוב, תחת הנחות סבירות מורכבות-תיאורטית). [94]
סוג למידה פסיבית זה הוא גם הסכימה הנפוצה ביותר בלמידה מפוקחת: אלגוריתם למידה לוקח בדרך כלל את דוגמאות ההדרכה קבועות, ללא יכולת לבצע שאילתות על התווית של דוגמאות ללא תווית. פלטת השערה h היא שלב של אינדוקציה. באופן קלאסי, מודל אינדוקטיבי מתפצל לשלב אימון ושלב יישום: פרמטרי המודל מוערכים בשלב האימון, והמודל הנלמד מיושם באופן שרירותי פעמים רבות בשלב היישום. במגבלה האסימפטוטית של מספר היישומים, פיצול שלבים זה קיים גם עם משאבים קוונטיים. [97]
יישומים וניסויים
[עריכת קוד מקור | עריכה]הניסויים המוקדמים ביותר נערכו באמצעות המחשב הקוונטי האדיאבטי D-Wave, למשל, כדי לזהות מכוניות בתמונות דיגיטליות תוך שימוש בהגברה מסודרת עם פונקציה אובייקטיבית לא קמורה בהדגמה ב-2009. [98] ניסויים רבים באו בעקבות אותה ארכיטקטורה, וחברות טכנולוגיה מובילות גילו עניין בפוטנציאל של למידת מכונות קוונטיות עבור יישומים טכנולוגיים עתידיים. בשנת 2013, גוגל מחקר, נאס"א ואיגוד חקר החלל של אוניברסיטאות השיקו את מעבדת הבינה המלאכותית הקוונטית אשר בוחנת את השימוש במחשב הקוונטי האדיאבטי D-Wave. דוגמה עדכנית יותר אימנה מודלים יצירתיים הסתברותיים עם קישוריות זוגנית שרירותית, והראתה שהמודל שלהם מסוגל ליצור ספרות בכתב יד כמו גם לשחזר תמונות רועשות של פסים ופסים וספרות בכתב יד. [59]
באמצעות טכנולוגיית חישול שונה המבוססת על תהודה מגנטית גרעינית (NMR), יושמה בשנת 2009 רשת הופפילד קוונטית שמיפתה את נתוני הקלט ושיננה נתונים למילטון, מה שמאפשר שימוש בחישוב קוונטי אדיאבטי. [99] טכנולוגיית NMR מאפשרת גם מחשוב קוונטי אוניברסלי,
שגיאות פרמטריות בתבנית:מקור
שימוש בפרמטרים מיושנים [ תאריך ] [דרוש מקור]</link> והוא שימש ליישום הניסיוני הראשון של מכונת וקטור תמיכה קוונטית כדי להבחין בין המספר '6' ו-'9' בכתב יד במחשב קוונטי במצב נוזלי בשנת 2015. [100] נתוני האימון כללו עיבוד מקדים של התמונה אשר ממפה אותם לוקטורים דו-מימדיים מנורמלים כדי לייצג את התמונות כמצבים של קיוביט. שני הערכים של הווקטור הם היחס האנכי והאופקי של עוצמת הפיקסלים של התמונה. לאחר שהווקטורים הוגדרו במרחב התכונה, הוטמעה מכונת וקטור התמיכה הקוונטית כדי לסווג את וקטור הקלט הלא ידוע. הקריאה מונעת טומוגרפיה קוונטית יקרה על ידי קריאת המצב הסופי במונחים של כיוון (מעלה/מטה) של אות ה-NMR.
יישומים פוטוניים מושכים יותר תשומת לב, [101] לא מעט משום שהם אינם דורשים קירור נרחב. זיהוי ספרות מדוברות ורמקולים בו-זמנית וחיזוי כאוטי של סדרות זמן הוכחו בקצבי נתונים מעבר ל-1 גיגה-בייט לשנייה בשנת 2013. [102] באמצעות פוטוניקה לא-לינארית כדי ליישם מסווג ליניארי אופטי, מודל פרצפטרון היה מסוגל ללמוד את גבול הסיווג באופן איטרטיבי מנתוני אימון באמצעות כלל משוב. [103] אבן בניין הליבה באלגוריתמי למידה רבים היא חישוב המרחק בין שני וקטורים: זה הוכח לראשונה בניסוי עבור עד שמונה ממדים באמצעות קיוביטים מסתבכים במחשב קוונטי פוטוני בשנת 2015. [104]
לאחרונה, בהתבסס על גישה נוירו-מימטית, נוסף מרכיב חדש לתחום למידת מכונה קוונטית, בצורה של מה שנקרא ממריסטור קוונטי, מודל קוונטי של הממריסטור הקלאסי הסטנדרטי. [105] ניתן לבנות מכשיר זה באמצעות נגד שניתן לכוונן, מדידות חלשות על המערכת ומנגנון הזנה קדימה קלאסי. הוצע יישום של ממריסטור קוונטי במעגלים מוליכים, [106] ובוצע ניסוי עם נקודות קוונטיות. [107] ממריסטור קוונטי יישם אינטראקציות לא ליניאריות בדינמיקה הקוונטית אשר תסייע בחיפוש אחר רשת עצבית קוונטית מתפקדת במלואה.
מאז 2016, IBM השיקה פלטפורמה מקוונת מבוססת ענן עבור מפתחי תוכנה קוונטית, הנקראת IBM Q Experience . פלטפורמה זו מורכבת ממספר מעבדים קוונטיים הפועלים במלואם, הנגישים באמצעות IBM Web API. בכך, החברה מעודדת מפתחי תוכנה לחפש אלגוריתמים חדשים באמצעות סביבת פיתוח עם יכולות קוונטיות. ארכיטקטורות חדשות נחקרות על בסיס ניסיוני, עד 32 קיוביטים, תוך שימוש בשיטות מחשוב קוונטי לכודים והן על מוליכים.
באוקטובר 2019, צוין כי להכנסת מחוללי מספרים אקראיים (QRNGs) למודלים של למידת מכונה, כולל רשתות עצביות ורשתות עצביות Convolutional עבור חלוקת משקל ראשונית אקראית ויערות אקראיים עבור תהליכי פיצול, הייתה השפעה עמוקה על יכולתם בהשוואה השיטה הקלאסית של Pseudorandom Number Generators (PRNGs). [108] עם זאת, בפרסום עדכני יותר משנת 2021, לא ניתן היה לשחזר את הטענות הללו לאתחול משקל רשת עצבית ולא נמצא יתרון משמעותי בשימוש ב-QRNGs על פני PRNGs. [109] העבודה גם הדגימה שיצירת מספרים אקראיים הוגנים עם מחשב קוונטי של שער היא משימה לא טריוויאלית במכשירי NISQ, ולכן בדרך כלל הרבה יותר קשה להשתמש ב-QRNGs בפועל מאשר ב-PRNGs.
מאמר שפורסם בדצמבר 2018 דיווח על ניסוי באמצעות מערכת יונים לכודים, המדגים זירוז קוונטי של זמן ההתלבטות של סוכני למידת חיזוק המשתמשים בחומרה קוונטית פנימית. [53]
במרץ 2021, צוות חוקרים מאוסטריה, הולנד, ארה"ב וגרמניה דיווח על הדגמה ניסיונית של האצה קוונטית של זמן הלמידה של סוכני למידת חיזוק המקיימים אינטראקציה קוונטית מלאה עם הסביבה. [110] [54] דרגות החופש הרלוונטיות הן של הסוכן והן של הסביבה מומשו על מעבד ננו-פוטוני משולב קומפקטי וניתן לכוונון מלא.
סַפקָנוּת
[עריכת קוד מקור | עריכה]בעוד שלמידת מכונה עצמה היא כיום לא רק תחום מחקר אלא תעשייה משמעותית וצומחת במהירות כלכלית ומחשוב קוונטי הוא תחום מבוסס היטב של מחקר תיאורטי וניסיוני כאחד, למידת מכונה קוונטית נותרה תחום לימודים תיאורטי בלבד. ניסיונות להדגים באופן ניסיוני מושגים של למידת מכונה קוונטית נותרו לא מספיקים.
שגיאות פרמטריות בתבנית:מקור
שימוש בפרמטרים מיושנים [ תאריך ] [דרוש מקור]</link>[ <span title="This claim needs references to reliable sources. (December 2020)">צריך ציטוט</span> ]
רבים מהמדענים המובילים שמפרסמים בהרחבה בתחום למידת מכונות קוונטיות מזהירים מפני ההייפ הנרחב סביב הנושא ומאופקים מאוד אם נשאלים לגבי השימושים המעשיים שלו בעתיד הנראה לעין. סופיה חן [111] אספה כמה מההצהרות שנאמרו על ידי מדענים ידועים בתחום:
- "אני חושבת שעדיין לא הכנו את שיעורי הבית שלנו. זהו תחום מדעי חדש ביותר," - הפיזיקאית מריה שולד מהסטארט-אפ המחשוב הקוונטי קנדו, Xanadu.
- "כאשר מערבבים למידת מכונה עם 'קוונטי', אתה מזרז הייפ-קונדנסט." [112] - יעקב ביאמונטה תורם לתורת החישוב הקוונטי.
- "יש עוד הרבה עבודה שצריך לעשות לפני שטענה שלמידת מכונות קוונטיות אכן תעבוד", - מדען המחשב Iordanis Kerenidis, ראש האלגוריתמים הקוונטיים בסטארט-אפ המחשוב הקוונטי QC Ware, המבוסס על עמק הסיליקון.
- "לא ראיתי ולו ראיה אחת לכך שקיימת משימה משמעותית [למידת מכונה] שעבורה יהיה הגיוני להשתמש במחשב קוונטי ולא במחשב קלאסי," - הפיזיקאי ריאן סווק מהאוניברסיטה החופשית של ברלין בגרמניה. .
- "אל תיפול על ההייפ!" - פרנק זיקרט, שהוא המחבר של הספר המעשי ביותר הקשור לנושא, היזהר ש"מחשבים קוונטיים רחוקים מקידום למידת מכונה עבור יכולת הייצוג שלהם", ואפילו מדבר על הערכה ואופטימיזציה לכל סוג של משימה קוונטית שימושית. עליונות עדיין לא הושגה. יתרה מזאת, אף אחד מהחוקרים הפעילים בתחום לא עושה תחזיות לגבי מתי זה יכול להיות מעשי.
שגיאות פרמטריות בתבנית:מקור
שימוש בפרמטרים מיושנים [ תאריך ] [דרוש מקור]</link>[ <span title="This claim needs references to reliable sources. (December 2020)">צריך ציטוט</span> ]
ראה גם
[עריכת קוד מקור | עריכה]- תכנות ניתן להבדיל
- מחשוב קוונטי
- אלגוריתם קוונטי למערכות ליניאריות של משוואות
- חישול קוונטי
- רשת נוירונים קוונטית
- תמונה קוונטית
הפניות
[עריכת קוד מקור | עריכה]תבנית:Quantum computingתבנית:Differentiable computingתבנית:Emerging technologies [[קטגוריה:חישוב קוונטי]] [[קטגוריה:למידת מכונה]]
- ^ Ventura, Dan (2000). "Quantum Associative Memory". Information Sciences. 124 (1–4): 273–296. arXiv:quant-ph/9807053. doi:10.1016/S0020-0255(99)00101-2.
- ^ 1 2 Trugenberger, Carlo A. (2001). "Probabilistic Quantum Memories". Physical Review Letters. 87 (6): 067901. arXiv:quant-ph/0012100. Bibcode:2001PhRvL..87f7901T. doi:10.1103/PhysRevLett.87.067901. PMID 11497863.
- ^ 1 2 Trugenberger, Carlo A. (2002). "Quantum Pattern Recognition". Quantum Information Processing. 1 (6): 471–493. doi:10.1023/A:1024022632303.
- ^ 1 2 Trugenberger, C. A. (2002-12-19). "Phase Transitions in Quantum Pattern Recognition". Physical Review Letters. 89 (27): 277903. arXiv:quant-ph/0204115. Bibcode:2002PhRvL..89A7903T. doi:10.1103/physrevlett.89.277903. ISSN 0031-9007. PMID 12513243.
- ^ Biamonte, Jacob; Wittek, Peter; Nicola, Pancotti; Rebentrost, Patrick; Wiebe, Nathan; Lloyd, Seth (2017). "Quantum machine learning". Nature. 549 (7671): 195–202. arXiv:1611.09347. Bibcode:2017Natur.549..195B. doi:10.1038/nature23474. PMID 28905917.
- ^ Schuld, Maria; Petruccione, Francesco (2018). Supervised Learning with Quantum Computers. Quantum Science and Technology. Bibcode:2018slqc.book.....S. doi:10.1007/978-3-319-96424-9. ISBN 978-3-319-96423-2.
- ^ 1 2 Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2014). "An introduction to quantum machine learning". Contemporary Physics. 56 (2): 172–185. arXiv:1409.3097. Bibcode:2015ConPh..56..172S. CiteSeerX 10.1.1.740.5622. doi:10.1080/00107514.2014.964942.
- ^ Wittek, Peter (2014). Quantum Machine Learning: What Quantum Computing Means to Data Mining. Academic Press. ISBN 978-0-12-800953-6.
- ^ 1 2 Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta (2014). "Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning". Quantum Information & Computation. 15 (3): 0318–0358. arXiv:1401.2142.
- ^ Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2013). "Quantum algorithms for supervised and unsupervised machine learning". arXiv:1307.0411 [quant-ph].
- ^ Yoo, Seokwon; Bang, Jeongho; Lee, Changhyoup; Lee, Jinhyoung (2014). "A quantum speedup in machine learning: Finding a N-bit Boolean function for a classification". New Journal of Physics. 16 (10): 103014. arXiv:1303.6055. Bibcode:2014NJPh...16j3014Y. doi:10.1088/1367-2630/16/10/103014.
- ^ Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2014-10-15). "An introduction to quantum machine learning". Contemporary Physics (באנגלית). 56 (2): 172–185. arXiv:1409.3097. Bibcode:2015ConPh..56..172S. CiteSeerX 10.1.1.740.5622. doi:10.1080/00107514.2014.964942. ISSN 0010-7514.
- ^ Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2017-11-30). "Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models". Physical Review X. 7 (4): 041052. arXiv:1609.02542. Bibcode:2017PhRvX...7d1052B. doi:10.1103/PhysRevX.7.041052. ISSN 2160-3308.
- ^ Farhi, Edward; Neven, Hartmut (2018-02-16). "Classification with Quantum Neural Networks on Near Term Processors". arXiv:1802.06002 [quant-ph].
- ^ Schuld, Maria; Bocharov, Alex; Svore, Krysta; Wiebe, Nathan (2020). "Circuit-centric quantum classifiers". Physical Review A. 101 (3): 032308. arXiv:1804.00633. Bibcode:2020PhRvA.101c2308S. doi:10.1103/PhysRevA.101.032308.
- ^ Yu, Shang; Albarran-Arriagada, F.; Retamal, J. C.; Wang, Yi-Tao; Liu, Wei; Ke, Zhi-Jin; Meng, Yu; Li, Zhi-Peng; Tang, Jian-Shun (2018-08-28). "Reconstruction of a Photonic Qubit State with Quantum Reinforcement Learning". Advanced Quantum Technologies. 2 (7–8): 1800074. arXiv:1808.09241. doi:10.1002/qute.201800074.
- ^ Ghosh, Sanjib; Opala, A.; Matuszewski, M.; Paterek, T.; Liew, Timothy C. H. (2019). "Quantum reservoir processing". npj Quantum Information. 5: 35. arXiv:1811.10335. Bibcode:2019npjQI...5...35G. doi:10.1038/s41534-019-0149-8.
- ^ Broecker, Peter; Assaad, Fakher F.; Trebst, Simon (2017-07-03). "Quantum phase recognition via unsupervised machine learning". arXiv:1707.00663 [cond-mat.str-el].
- ^ 1 2 Huembeli, Patrick; Dauphin, Alexandre; Wittek, Peter (2018). "Identifying Quantum Phase Transitions with Adversarial Neural Networks". Physical Review B. 97 (13): 134109. arXiv:1710.08382. Bibcode:2018PhRvB..97m4109H. doi:10.1103/PhysRevB.97.134109. ISSN 2469-9950.
- ^ 1 2 Krenn, Mario (2016-01-01). "Automated Search for new Quantum Experiments". Physical Review Letters. 116 (9): 090405. arXiv:1509.02749. Bibcode:2016PhRvL.116i0405K. doi:10.1103/PhysRevLett.116.090405. PMID 26991161.
- ^ Knott, Paul (2016-03-22). "A search algorithm for quantum state engineering and metrology". New Journal of Physics. 18 (7): 073033. arXiv:1511.05327. Bibcode:2016NJPh...18g3033K. doi:10.1088/1367-2630/18/7/073033.
- ^ Dunjko, Vedran; Briegel, Hans J (2018-06-19). "Machine learning & artificial intelligence in the quantum domain: a review of recent progress". Reports on Progress in Physics. 81 (7): 074001. arXiv:1709.02779. Bibcode:2018RPPh...81g4001D. doi:10.1088/1361-6633/aab406. ISSN 0034-4885. PMID 29504942.
{{cite journal}}:|hdl-access=requires|hdl=(עזרה) - ^ Huggins, William; Patel, Piyush; Whaley, K. Birgitta; Stoudenmire, E. Miles (2018-03-30). "Towards Quantum Machine Learning with Tensor Networks". Quantum Science and Technology. 4 (2): 024001. arXiv:1803.11537. doi:10.1088/2058-9565/aaea94.
- ^ Carleo, Giuseppe; Nomura, Yusuke; Imada, Masatoshi (2018-02-26). "Constructing exact representations of quantum many-body systems with deep neural networks". Nature Communications. 9 (1): 5322. arXiv:1802.09558. Bibcode:2018NatCo...9.5322C. doi:10.1038/s41467-018-07520-3. PMC 6294148. PMID 30552316.
- ^ Bény, Cédric (2013-01-14). "Deep learning and the renormalization group". arXiv:1301.3124 [quant-ph].
- ^ Arunachalam, Srinivasan; de Wolf, Ronald (2017-01-24). "A Survey of Quantum Learning Theory". arXiv:1701.06806 [quant-ph].
- ^ Sergioli, Giuseppe; Giuntini, Roberto; Freytes, Hector (2019-05-09). "A new Quantum approach to binary classification". PLOS ONE. 14 (5): e0216224. Bibcode:2019PLoSO..1416224S. doi:10.1371/journal.pone.0216224. PMC 6508868. PMID 31071129.
- ^ Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (2006-06-07). "Machine Learning in a Quantum World". Advances in Artificial Intelligence. Lecture Notes in Computer Science (באנגלית). Vol. 4013. pp. 431–442. doi:10.1007/11766247_37. ISBN 978-3-540-34628-9.
- ^ 1 2 3 Dunjko, Vedran; Taylor, Jacob M.; Briegel, Hans J. (2016-09-20). "Quantum-Enhanced Machine Learning". Physical Review Letters. 117 (13): 130501. arXiv:1610.08251. Bibcode:2016PhRvL.117m0501D. doi:10.1103/PhysRevLett.117.130501. PMID 27715099.
- ^ 1 2 Rebentrost, Patrick; Mohseni, Masoud; Lloyd, Seth (2014). "Quantum Support Vector Machine for Big Data Classification". Physical Review Letters. 113 (13): 130503. arXiv:1307.0471. Bibcode:2014PhRvL.113m0503R. doi:10.1103/PhysRevLett.113.130503. PMID 25302877.
- ^ 1 2 Wiebe, Nathan; Braun, Daniel; Lloyd, Seth (2012). "Quantum Algorithm for Data Fitting". Physical Review Letters. 109 (5): 050505. arXiv:1204.5242. Bibcode:2012PhRvL.109e0505W. doi:10.1103/PhysRevLett.109.050505. PMID 23006156.
- ^ 1 2 Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2016). "Prediction by linear regression on a quantum computer". Physical Review A. 94 (2): 022342. arXiv:1601.07823. Bibcode:2016PhRvA..94b2342S. doi:10.1103/PhysRevA.94.022342.
- ^ Harrow, Aram W.; Hassidim, Avinatan; Lloyd, Seth (2008). "Quantum algorithm for solving linear systems of equations". Physical Review Letters. 103 (15): 150502. arXiv:0811.3171. Bibcode:2009PhRvL.103o0502H. doi:10.1103/PhysRevLett.103.150502. PMID 19905613.
- ^ Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2014). "Quantum principal component analysis". Nature Physics. 10 (9): 631. arXiv:1307.0401. Bibcode:2014NatPh..10..631L. CiteSeerX 10.1.1.746.480. doi:10.1038/nphys3029.
- ^ Zhao, Zhikuan; Fitzsimons, Jack K.; Fitzsimons, Joseph F. (2019). "Quantum assisted Gaussian process regression". Physical Review A. 99 (5): 052331. arXiv:1512.03929. Bibcode:2019PhRvA..99e2331Z. doi:10.1103/PhysRevA.99.052331.
- ^ Soklakov, Andrei N.; Schack, Rüdiger (2006). "Efficient state preparation for a register of quantum bits". Physical Review A. 73 (1): 012307. arXiv:quant-ph/0408045. Bibcode:2006PhRvA..73a2307S. doi:10.1103/PhysRevA.73.012307.
- ^ Giovannetti, Vittorio; Lloyd, Seth; MacCone, Lorenzo (2008). "Quantum Random Access Memory". Physical Review Letters. 100 (16): 160501. arXiv:0708.1879. Bibcode:2008PhRvL.100p0501G. doi:10.1103/PhysRevLett.100.160501. PMID 18518173.
- ^ Aaronson, Scott (2015). "Read the fine print". Nature Physics. 11 (4): 291–293. Bibcode:2015NatPh..11..291A. doi:10.1038/nphys3272.
- ^ Bang, Jeongho; Dutta, Arijit; Lee, Seung-Woo; Kim, Jaewan (2019). "Optimal usage of quantum random access memory in quantum machine learning". Physical Review A. 99 (1): 012326. arXiv:1809.04814. Bibcode:2019PhRvA..99a2326B. doi:10.1103/PhysRevA.99.012326.
- ^ "Quantum Computing: The Next Big Thing For Finance By 2024". נבדק ב-2023-06-17.
- ^ "Classical Computing vs Quantum Computing". GeeksforGeeks (באנגלית אמריקאית). 2019-06-12. נבדק ב-2023-06-17.
- ^ Griol-Barres, Israel; Milla, Sergio; Cebrián, Antonio; Mansoori, Yashar; Millet, José (בינואר 2021). "Variational Quantum Circuits for Machine Learning. An Application for the Detection of Weak Signals". Applied Sciences (באנגלית). 11 (14): 6427. doi:10.3390/app11146427. ISSN 2076-3417.
{{cite journal}}: (עזרה);|hdl-access=requires|hdl=(עזרה) - ^ Chen, Samuel Yen-Chi; Yang, Chao-Han Huck; Qi, Jun; Chen, Pin-Yu; Ma, Xiaoli; Goan, Hsi-Sheng (2020). "Variational Quantum Circuits for Deep Reinforcement Learning". IEEE Access. 8: 141007–141024. arXiv:1907.00397. Bibcode:2020IEEEA...8n1007C. doi:10.1109/ACCESS.2020.3010470. ISSN 2169-3536.
- ^ Park, Daniel K.; Blank, Carsten; Petruccione, Francesco (2020-07-27). "The theory of the quantum kernel-based binary classifier". Physics Letters A (באנגלית). 384 (21): 126422. arXiv:2004.03489. Bibcode:2020PhLA..38426422P. doi:10.1016/j.physleta.2020.126422. ISSN 0375-9601.
- ^ Yi, Teng; Wang, Jie; Xu, Fufang (2021-08-01). "Binary classification of single qubits using quantum machine learning method". Journal of Physics: Conference Series. 2006 (1): 012020. doi:10.1088/1742-6596/2006/1/012020. ISSN 1742-6588.
- ^ Maheshwari, Danyal; Sierra-Sosa, Daniel; Garcia-Zapirain, Begonya (2022). "Variational Quantum Classifier for Binary Classification: Real vs Synthetic Dataset". IEEE Access. 10: 3705–3715. Bibcode:2022IEEEA..10.3705M. doi:10.1109/ACCESS.2021.3139323. ISSN 2169-3536.
- ^ 1 2 Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (2013-02-01). "Quantum speed-up for unsupervised learning". Machine Learning (באנגלית). 90 (2): 261–287. doi:10.1007/s10994-012-5316-5. ISSN 0885-6125.
- ^ Paparo, Giuseppe Davide; Martin-Delgado, Miguel Angel (2012). "Google in a Quantum Network". Scientific Reports. 2 (444): 444. arXiv:1112.2079. Bibcode:2012NatSR...2E.444P. doi:10.1038/srep00444. PMC 3370332. PMID 22685626.
- ^ 1 2 3 4 Paparo, Giuseppe Davide; Dunjko, Vedran; Makmal, Adi; Martin-Delgado, Miguel Angel; Briegel, Hans J. (2014). "Quantum Speedup for Active Learning Agents". Physical Review X. 4 (3): 031002. arXiv:1401.4997. Bibcode:2014PhRvX...4c1002P. doi:10.1103/PhysRevX.4.031002.
- ^ Dong, Daoyi; Chen, Chunlin; Li, Hanxiong; Tarn, Tzyh-Jong (2008). "Quantum Reinforcement Learning". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 38 (5): 1207–1220. arXiv:0810.3828. CiteSeerX 10.1.1.243.5369. doi:10.1109/TSMCB.2008.925743. PMID 18784007.
- ^ Dunjko, Vedran; Friis, Nicolai; Briegel, Hans J. (2015-01-01). "Quantum-enhanced deliberation of learning agents using trapped ions". New Journal of Physics (באנגלית). 17 (2): 023006. arXiv:1407.2830. Bibcode:2015NJPh...17b3006D. doi:10.1088/1367-2630/17/2/023006. ISSN 1367-2630.
- ^ Lamata, Lucas (2017). "Basic protocols in quantum reinforcement learning with superconducting circuits". Scientific Reports. 7 (1): 1609. arXiv:1701.05131. Bibcode:2017NatSR...7.1609L. doi:10.1038/s41598-017-01711-6. PMC 5431677. PMID 28487535.
- ^ 1 2 Sriarunothai, Theeraphot; Wölk, Sabine; Giri, Gouri Shankar; Friis, Nicolai; Dunjko, Vedran; Briegel, Hans J.; Wunderlich, Christof (2019). "Speeding-up the decision making of a learning agent using an ion trap quantum processor". Quantum Science and Technology (באנגלית). 4 (1): 015014. arXiv:1709.01366. Bibcode:2019QS&T....4a5014S. doi:10.1088/2058-9565/aaef5e. ISSN 2058-9565.
- ^ 1 2 3 Saggio, Valeria; Asenbeck, Beate; Hamann, Arne; Strömberg, Teodor; Schiansky, Peter; Dunjko, Vedran; Friis, Nicolai; Harris, Nicholas C.; Hochberg, Michael; Englund, Dirk; Wölk, Sabine (10 במרץ 2021). "Experimental quantum speed-up in reinforcement learning agents". Nature (באנגלית). 591 (7849): 229–233. arXiv:2103.06294. Bibcode:2021Natur.591..229S. doi:10.1038/s41586-021-03242-7. ISSN 1476-4687. PMC 7612051. PMID 33692560.
{{cite journal}}: (עזרה) - ^ Biswas, Rupak; Jiang, Zhang; Kechezi, Kostya; Knysh, Sergey; Mandrà, Salvatore; O’Gorman, Bryan; Perdomo-Ortiz, Alejando; Pethukov, Andre; Realpe-Gómez, John; Rieffel, Eleanor; Venturelli, Davide (2016). "A NASA perspective on quantum computing: Opportunities and challenges". Parallel Computing. 64: 81–98. arXiv:1704.04836. doi:10.1016/j.parco.2016.11.002.
- ^ Adachi. "Application of quantum annealing to training of deep neural networks". arXiv:1510.06356.
- ^ 1 2 Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2016). "Estimation of effective temperatures in quantum annealers for sampling applications: A case study with possible applications in deep learning". Physical Review A. 94 (2): 022308. arXiv:1510.07611. Bibcode:2016PhRvA..94b2308B. doi:10.1103/PhysRevA.94.022308.
- ^ Korenkevych. "Benchmarking quantum hardware for training of fully visible Boltzmann machines". arXiv:1611.04528.
- ^ 1 2 3 Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2017). "Quantum-assisted learning of graphical models with arbitrary pairwise connectivity". Physical Review X. 7 (4): 041052. arXiv:1609.02542. Bibcode:2017PhRvX...7d1052B. doi:10.1103/PhysRevX.7.041052.
- ^ Rocutto, Lorenzo; Destri, Claudio; Prati, Enrico (2021). "Quantum Semantic Learning by Reverse Annealing of an Adiabatic Quantum Computer". Advanced Quantum Technologies. 4 (2): 2000133. arXiv:2003.11945. doi:10.1002/qute.202000133. ISSN 2511-9044.
- ^ Amin, Mohammad H.; Andriyash, Evgeny; Rolfe, Jason; Kulchytskyy, Bohdan; Melko, Roger (2018). "Quantum Boltzmann machines". Phys. Rev. X. 8 (21050): 021050. arXiv:1601.02036. Bibcode:2018PhRvX...8b1050A. doi:10.1103/PhysRevX.8.021050.
- ^ "Phys. Rev. E 72, 026701 (2005): Quantum annealing in a kinetically co…". archive.is. 2014-01-13. אורכב מ-המקור ב-2014-01-13. נבדק ב-2018-12-07.
- ^ Wittek, Peter; Gogolin, Christian (2017). "Quantum Enhanced Inference in Markov Logic Networks". Scientific Reports. 7 (45672): 45672. arXiv:1611.08104. Bibcode:2017NatSR...745672W. doi:10.1038/srep45672. PMC 5395824. PMID 28422093.
- ^ 1 2 3 4 Gupta, Sanjay; Zia, R.K.P. (2001-11-01). "Quantum Neural Networks". Journal of Computer and System Sciences (באנגלית). 63 (3): 355–383. arXiv:quant-ph/0201144. doi:10.1006/jcss.2001.1769. ISSN 0022-0000.
- ^ 1 2 Ezhov, Alexandr A.; Ventura, Dan (2000), "Quantum Neural Networks", Future Directions for Intelligent Systems and Information Sciences, Studies in Fuzziness and Soft Computing (באנגלית), Physica-Verlag HD, 45: 213–235, doi:10.1007/978-3-7908-1856-7_11, ISBN 978-3-7908-2470-4
- ^ 1 2 Behrman, E.C.; Nash, L.R.; Steck, J.E.; Chandrashekar, V.G.; Skinner, S.R. (2000-10-01). "Simulations of quantum neural networks". Information Sciences (באנגלית). 128 (3–4): 257–269. doi:10.1016/S0020-0255(00)00056-6. ISSN 0020-0255.
- ^ Henderson, Maxwell; Shakya, Samriddhi; Pradhan, Shashindra; Cook, Tristan (2020-02-27). "Quanvolutional neural networks: powering image recognition with quantum circuits". Quantum Machine Intelligence. 2 (1). arXiv:1904.04767. doi:10.1007/s42484-020-00012-y. ISSN 2524-4906.
- ^ Gaikwad, Akash S. Pruning convolution neural network (SqueezeNet) for efficient hardware deployment. OCLC 1197735354.
- ^ Cong, Iris; Choi, Soonwon; Lukin, Mikhail D. (2019-08-26). "Quantum convolutional neural networks". Nature Physics. 15 (12): 1273–1278. arXiv:1810.03787. Bibcode:2019NatPh..15.1273C. doi:10.1038/s41567-019-0648-8. ISSN 1745-2473.
- ^ Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. (2018-09-10). "Quantum circuit learning". Physical Review A. 98 (3): 032309. arXiv:1803.00745. Bibcode:2018PhRvA..98c2309M. doi:10.1103/physreva.98.032309. ISSN 2469-9926.
- ^ Hochreiter, Sepp; Schmidhuber, Jürgen (1997-11-01). "Long Short-Term Memory". Neural Computation. 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735. ISSN 0899-7667. PMID 9377276.
- ^ Preskill, John (2018-08-06). "Quantum Computing in the NISQ era and beyond". Quantum. 2: 79. arXiv:1801.00862. Bibcode:2018Quant...2...79P. doi:10.22331/q-2018-08-06-79. ISSN 2521-327X.
- ^ Bacon, Dave (2013-09-12), "Experimental quantum error correction", Quantum Error Correction, Cambridge University Press: 509–518, doi:10.1017/cbo9781139034807.023, ISBN 9780521897877, נבדק ב-2022-11-23
- ^ Bharti, Kishor; Cervera-Lierta, Alba; Kyaw, Thi Ha; Haug, Tobias; Alperin-Lea, Sumner; Anand, Abhinav; Degroote, Matthias; Heimonen, Hermanni; Kottmann, Jakob S.; Menke, Tim; Mok, Wai-Keong (2022-02-15). "Noisy intermediate-scale quantum algorithms". Reviews of Modern Physics. 94 (1): 015004. arXiv:2101.08448. Bibcode:2022RvMP...94a5004B. doi:10.1103/revmodphys.94.015004. ISSN 0034-6861.
- ^ Grant, Edward; Benedetti, Marcello; Cao, Shuxiang; Hallam, Andrew; Lockhart, Joshua; Stojevic, Vid; Green, Andrew G.; Severini, Simone (בדצמבר 2018). "Hierarchical quantum classifiers". npj Quantum Information. 4 (1): 65. arXiv:1804.03680. Bibcode:2018npjQI...4...65G. doi:10.1038/s41534-018-0116-9.
{{cite journal}}: (עזרה) - ^ Zhao, Chen; Gao, Xiao-Shan (2021-06-04). "Analyzing the barren plateau phenomenon in training quantum neural networks with the ZX-calculus". Quantum. 5: 466. arXiv:2102.01828. Bibcode:2021Quant...5..466Z. doi:10.22331/q-2021-06-04-466. ISSN 2521-327X.
- ^ Hur, Tak; Kim, Leeseok; Park, Daniel K. (2022-02-10). "Quantum convolutional neural network for classical data classification". Quantum Machine Intelligence. 4 (1): 3. arXiv:2108.00661. doi:10.1007/s42484-021-00061-x. ISSN 2524-4906.
- ^ Ostaszewski, Mateusz; Grant, Edward; Benedetti, Marcello (2021-01-28). "Structure optimization for parameterized quantum circuits". Quantum. 5: 391. arXiv:1905.09692. Bibcode:2021Quant...5..391O. doi:10.22331/q-2021-01-28-391. ISSN 2521-327X.
- ^ J., Sharma, Kunal Cerezo, M. Cincio, Lukasz Coles, Patrick (2020-05-25). Trainability of Dissipative Perceptron-Based Quantum Neural Networks. OCLC 1228410830.
- ^ Clark, Lewis A.; Huang W., Wei; Barlow, Thomas H.; Beige, Almut (2015). "Hidden Quantum Markov Models and Open Quantum Systems with Instantaneous Feedback". In Sanayei, Ali; Rössler, Otto E.; Zelinka, Ivan (eds.). ISCS 2014: Interdisciplinary Symposium on Complex Systems. Emergence, Complexity and Computation. Vol. 14. pp. 131–151. CiteSeerX 10.1.1.749.3332. doi:10.1007/978-3-319-10759-2_16. ISBN 978-3-319-10759-2.
- ^ 1 2 3 Srinivasan, Siddarth; Gordon, Geoff; Boots, Byron (2018). "Learning Hidden Quantum Markov Models" (PDF). Aistats.
- ^ Sentís, Gael; Guţă, Mădălin; Adesso, Gerardo (9 ביולי 2015). "Quantum learning of coherent states". EPJ Quantum Technology. 2 (1). arXiv:1410.8700. doi:10.1140/epjqt/s40507-015-0030-4.
{{cite journal}}: (עזרה) - ^ Sasaki, Masahide; Carlini, Alberto (6 באוגוסט 2002). "Quantum learning and universal quantum matching machine". Physical Review A. 66 (2): 022303. arXiv:quant-ph/0202173. Bibcode:2002PhRvA..66b2303S. doi:10.1103/PhysRevA.66.022303.
{{cite journal}}: (עזרה) - ^ Bisio, Alessandro; Chiribella, Giulio; D’Ariano, Giacomo Mauro; Facchini, Stefano; Perinotti, Paolo (25 במרץ 2010). "Optimal quantum learning of a unitary transformation". Physical Review A. 81 (3): 032324. arXiv:0903.0543. Bibcode:2010PhRvA..81c2324B. doi:10.1103/PhysRevA.81.032324.
{{cite journal}}: (עזרה) - ^ Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (1 בינואר 2007). "Quantum clustering algorithms". Proceedings of the 24th international conference on Machine learning. pp. 1–8. CiteSeerX 10.1.1.80.9513. doi:10.1145/1273496.1273497. ISBN 978-1-59593-793-3.
{{cite book}}: (עזרה) - ^ Molnar, Christoph. Interpretable Machine Learning.
- ^ Schuld, Maria; Killoran, Nathan (2 במרץ 2022). "Is Quantum Advantage the Right Goal for Quantum Machine Learning?". PRX Quantum. 3 (3): 030101. arXiv:2203.01340. Bibcode:2022PRXQ....3c0101S. doi:10.1103/PRXQuantum.3.030101.
{{cite journal}}: (עזרה) - ^ Mercaldo, F.; Ciaramella, G.; Iadarola, G.; Storto, M.; Martinelli, F.; Santone, A.o (2022). "Towards Explainable Quantum Machine Learning for Mobile Malware Detection and Classification". Applied Sciences (באנגלית). 12: 12025. doi:10.3390/app122312025.
- ^ שגיאת ציטוט: תג
<ref>לא תקין; לא נכתב טקסט עבור הערות השוליים בשםxqml2023 - ^ Ribeiro, Marco Tulio; Singh, Sameer; Guestrin, Carlos (2016-08-09), "Why Should I Trust You?": Explaining the Predictions of Any Classifier, arXiv:1602.04938
- ^ Pira, Lirandë; Ferrie, Chris (2024-04-18), On the Interpretability of Quantum Neural Networks, arXiv:2308.11098
- ^ Cory, D. G.; Wiebe, Nathan; Ferrie, Christopher; Granade, Christopher E. (2012-07-06). "Robust Online Hamiltonian Learning". New Journal of Physics (באנגלית). 14 (10): 103013. arXiv:1207.1655. Bibcode:2012NJPh...14j3013G. doi:10.1088/1367-2630/14/10/103013.
- ^ Arunachalam. "A Survey of Quantum Learning Theory". arXiv:1701.06806.
- ^ 1 2 3 Servedio, Rocco A.; Gortler, Steven J. (2004). "Equivalences and Separations Between Quantum and Classical Learnability". SIAM Journal on Computing. 33 (5): 1067–1092. CiteSeerX 10.1.1.69.6555. doi:10.1137/S0097539704412910.
- ^ Arunachalam. "Optimal Quantum Sample Complexity of Learning Algorithms". arXiv:1607.00932.
- ^ Nader, Bshouty H.; Jeffrey, Jackson C. (1999). "Learning DNF over the Uniform Distribution Using a Quantum Example Oracle". SIAM Journal on Computing. 28 (3): 1136–1153. CiteSeerX 10.1.1.23.5709. doi:10.1137/S0097539795293123.
- ^ Monràs, Alex; Sentís, Gael; Wittek, Peter (2017). "Inductive supervised quantum learning". Physical Review Letters. 118 (19): 190503. arXiv:1605.07541. Bibcode:2017PhRvL.118s0503M. doi:10.1103/PhysRevLett.118.190503. PMID 28548536.
- ^ "NIPS 2009 Demonstration: Binary Classification using Hardware Implementation of Quantum Annealing" (PDF). Static.googleusercontent.com. נבדק ב-26 בנובמבר 2014.
{{cite web}}: (עזרה) - ^ Neigovzen, Rodion; Neves, Jorge L.; Sollacher, Rudolf; Glaser, Steffen J. (2009). "Quantum pattern recognition with liquid-state nuclear magnetic resonance". Physical Review A. 79 (4): 042321. arXiv:0802.1592. Bibcode:2009PhRvA..79d2321N. doi:10.1103/PhysRevA.79.042321.
- ^ Li, Zhaokai; Liu, Xiaomei; Xu, Nanyang; Du, Jiangfeng (2015). "Experimental Realization of a Quantum Support Vector Machine". Physical Review Letters. 114 (14): 140504. arXiv:1410.1054. Bibcode:2015PhRvL.114n0504L. doi:10.1103/PhysRevLett.114.140504. PMID 25910101.
- ^ Wan, Kwok-Ho; Dahlsten, Oscar; Kristjansson, Hler; Gardner, Robert; Kim, Myungshik (2017). "Quantum generalisation of feedforward neural networks". npj Quantum Information. 3 (36): 36. arXiv:1612.01045. Bibcode:2017npjQI...3...36W. doi:10.1038/s41534-017-0032-4.
- ^ Brunner, Daniel; Soriano, Miguel C.; Mirasso, Claudio R.; Fischer, Ingo (2013). "Parallel photonic information processing at gigabyte per second data rates using transient states". Nature Communications. 4: 1364. Bibcode:2013NatCo...4.1364B. doi:10.1038/ncomms2368. PMC 3562454. PMID 23322052.
- ^ Tezak, Nikolas; Mabuchi, Hideo (2015). "A coherent perceptron for all-optical learning". EPJ Quantum Technology. 2. arXiv:1501.01608. Bibcode:2015arXiv150101608T. doi:10.1140/epjqt/s40507-015-0023-3.
- ^ Cai, X.-D.; Wu, D.; Su, Z.-E.; Chen, M.-C.; Wang, X.-L.; Li, Li; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. (2015). "Entanglement-Based Machine Learning on a Quantum Computer". Physical Review Letters. 114 (11): 110504. arXiv:1409.7770. Bibcode:2015PhRvL.114k0504C. doi:10.1103/PhysRevLett.114.110504. PMID 25839250.
- ^ Pfeiffer, P.; Egusquiza, I. L.; Di Ventra, M.; Sanz, M.; Solano, E. (2016). "Quantum memristors". Scientific Reports. 6 (2016): 29507. arXiv:1511.02192. Bibcode:2016NatSR...629507P. doi:10.1038/srep29507. PMC 4933948. PMID 27381511.
- ^ Salmilehto, J.; Deppe, F.; Di Ventra, M.; Sanz, M.; Solano, E. (2017). "Quantum Memristors with Superconducting Circuits". Scientific Reports. 7 (42044): 42044. arXiv:1603.04487. Bibcode:2017NatSR...742044S. doi:10.1038/srep42044. PMC 5307327. PMID 28195193.
- ^ Li, Ying; Holloway, Gregory W.; Benjamin, Simon C.; Briggs, G. Andrew D.; Baugh, Jonathan; Mol, Jan A. (2017). "A simple and robust quantum memristor". Physical Review B. 96 (7): 075446. arXiv:1612.08409. Bibcode:2017PhRvB..96g5446L. doi:10.1103/PhysRevB.96.075446.
- ^ Bird, Jordan J.; Ekárt, Anikó; Faria, Diego R. (2019-10-28). "On the effects of pseudorandom and quantum-random number generators in soft computing". Soft Computing. Springer Science and Business Media LLC. 24 (12): 9243–9256. doi:10.1007/s00500-019-04450-0. ISSN 1432-7643.
- ^ Heese, Raoul; Wolter, Moritz; Mücke, Sascha; Franken, Lukas; Piatkowski, Nico (2024). "On the effects of biased quantum random numbers on the initialization of artificial neural networks". Machine Learning. 113 (3): 1189–1217. arXiv:2108.13329. doi:10.1007/s10994-023-06490-y.
- ^ "A quantum trick with photons gives machine learning a speed boost". New Scientist (באנגלית). נבדק ב-31 באוגוסט 2021.
{{cite news}}: (עזרה) - ^ "Can quantum machine learning move beyond its own hype?". Protocol (באנגלית). 2020-05-04. נבדק ב-2020-10-27.
- ^ "Can quantum machine learning move beyond its own hype?". quantamagazine.org (באנגלית). 2018-01-22.












