משתמש:Ariel1024/צבר מיקרוקנוני
מינוח מדוייק
[עריכת קוד מקור | עריכה]הביטוי המתמטי המדויק להרכב סטטיסטי תלוי בסוג המכניקה הנבדקת – קוונטית או קלאסית – מאחר שהרעיון של "מיקרו־מצב" שונה במידה ניכרת בשני מקרים אלה. במכניקת הקוואנטים, לכסון מספק קבוצה בדידה של מיקרומצבים עם אנרגיות ספציפיות. ואילו במקרה המכני הקלאסי יש לבצע אינטגרל על מרחב המצבים הקנוני ("מרחב הפזה", "phase space"), ואת גודל המיקרומצבים (העידון החלוקה) במרחב המצבים ניתן לבחור באופן שרירותי במקצת.
לשם בניית הצבר המיקרוקנוני, בכל אחת משתי המכניקות, יש להגדיר תחילה את טווח האנרגיה. בביטוי מטה הפונקציה (פונקציה של H, בעלת קיצון ב־Eעם רוחב ω)תשמש לייצוג טווח האנרגיה בו יכללו המצבים. An דוגמה לפונקציה מעין זו תהיה [1]
או פונקציה חלקה יותר,
המכניקה קוונטית
[עריכת קוד מקור | עריכה]במכניקת הקוונטים צברים מיוצגים על ידי מטריצת צפיפות, מסומנת על ידי . צבר מיקרוקנוני יכול להיכתב בסימון דיראק, בעזרת המצבים העצמיים של האנגיה והאנרגיות העצמיות במערכת. בהינתן בסיס שלם של מצבי־אנרגיה־עצמיים , הסדור לפי מפתח i, הצבר המיקרוקנוני ייוצג על ידי:[דרוש מקור]
כאשר Hi הן האנרגיות העצמיות הנקבעות על ידי (כאן Ĥ היא אופרטור האנרגיה הכוללת במערכת, כלומר אופרטור ההמילטוניאן). הערך של נקבע על פי הדרישה כי היא מטריצת צפיפות מנורמלת, כך ש־
פונקציית נפח המצבים (המשמשת לחישוב האנטרופיה) ניתנת על ידי
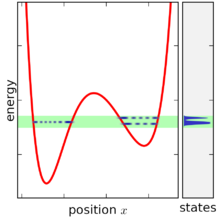
הצבר המיקרוקנוני מוגדר על ידי לקיחת הגבול של מטריצת הצפיפות כשרוחב טווח האנרגיה הולך לאפס, אולם מצב בעייתי מתרחש כאשר רוחב טווח האנרגיה הופך צר יותר המרווח בין רמות האנרגיה. עבור רוחב אנרגיה צר מאוד, הצבר איננו קיים כלל עבור רוב הערכים של E, שכן אין מצבים שמוכלים בטווח. כאשר הצבר כן קיים, הוא לרוב מכיל מצב אחד (או שניים), מאחר שבמערכת מורכבת רמות האנרגיה שוות אחת לשנייה רק באופן מקרי (ראו תורת המטריצות אקראיות, , לדיון נוסף בנושא זה). יותר מכך, העלייה של פונקציית נפח המצבים היא בדידה ולא רציפה ולכן ערכי הנגזרת שלה הם רק אפס או "אינסוף", מה שמקשה על הגדרת צפיפות המצבים. ניתן לפתור בעיה זו על ידי המנעות מלקיחת רוחב טווח האנרגיה לאפס באופן מוחלט והחלקה של פונקציית נפח המצבים, ברם זה הופך את הגדרת הצבר למסובכת עוד יותר, שכן זה מחייב לציין ולהתחשב ברוחב טווח האנרגיה בנוסף למשתנים אחרים (יחד: "צבר ").
במכניקה הקלאסית
[עריכת קוד מקור | עריכה]במכניקה קלסית, צבר מיוצג על ידי פונקצית צפיפות־הסתברות משותפת המוגדרת על מרחב הפזה של המערכת.[1] במרחב הפזה יש n קואורדינטות מוכללות המסומנות ב־, ו־n משתני התנע הצמודים־קנונית שלהן, . פונקצית צפיפות הסתברות של הצבר המקרוקנוני היא:
כאשר
- היא האנרגיה הכוללת (ההמילטוניאנית) של המערכת, פונקציה של המצב (הפזה)
- הוא קבוע שרירותי בעל יחידות של זמן×אנרגיה, setting the extent of one microstate and providing correct dimensions to .[note 1]
- is an overcounting correction factor, often used for particle systems where identical particles are able to change place with each other.[note 2]
Again, the value of is determined by demanding that is a normalized probability density function:
This integral is taken over the entire phase space. The state volume function (used to calculate entropy) is defined by
As the energy width ω is taken to zero, the value of decreases in proportion to ω as W = ω (dv/dE).
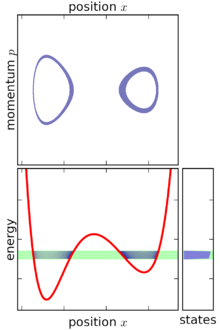
Based on the above definition, the microcanonical ensemble can be visualized as an infinitesimally thin shell in phase space, centered on a constant-energy surface. Although the microcanonical ensemble is confined to this surface, it is not necessarily uniformly distributed over that surface: if the gradient of energy in phase space varies, then the microcanonical ensemble is "thicker" (more concentrated) in some parts of the surface than others. This feature is an unavoidable consequence of requiring that the microcanonical ensemble is a steady-state ensemble.
שגיאת ציטוט: קיימים תגי <ref> עבור קבוצה בשם "note", אך לא נמצא תג <references group="note"/> מתאים.