משתמש:גלעד ניר/דף טיוטה
בלוגיקה ובלוגיקה מתמטית, תחשיב פרדיקטים מסדר ראשון הוא מערכת אקסיומטית המאפשרת לטפל בפסוקים שהמבנה הבסיסי שלהן כולל נשואים (פרדיקטים) החלים על אובייקטים, או על משתנים שערכיהם הם אובייקטים. הפרדיקטים עצמם הם פונקציות המחזירות ערך אמת (אמיתי או שקרי) עבור אובייקטים מסויימים או עבור משתנים מסויימים.
פסוקים יסודיים בתחשיב הפרדיקטים
[עריכת קוד מקור | עריכה]בתחשיב הפרדיקטים הטענה האטומית היא בעלת שני חלקים בלבד, פרדיקט ואובייקט, החוברים זה לזה כפי שפונקציה חלה על משתנים. למשל, את המשפט "דני הוא חכם", מצרינים (מביע באופן צורני) כך:
כאשר P מציין את הפרדיקט חכם, ו-a מציין את שמו של האובייקט, דני. תחשיב הפרדיקטים מאפשר גם להביע יחסים בין שני אובייקטים או יותר באמצעות פרדיקטים דו מקומיים, המקבלים שני אובייקטים. למשל כדי לומר שדני (a) הוא חבר של רני (b), תוך ציון יחס החברות באמצעות האות R, נקבל את הנוסחה הבאה:
תחשיב הפרדיקטים מסדר ראשון כולל גם שני אמצעי הכימות (קוונטיפיקציה). את הכמת ניתן להבין כפונקציה מסדר גבוה יותר החלה על הפרדיקט ועל המשתנה שלו. למשל, כך מובעת בתחשיב הפרדיקטים צורתה של הטענה "כל דבר הוא חכם":
וכך מובעת את הטענה "יש דבר אחד לפחות שהוא חכם":
כוחו של תחשיב הפרדיקטים ניכר ביכולתו להביע את קשרי ההיסק הלוגיים בין טענות שונות. למשל, ניתן להראות באמצעותו כי הטיעון הבא הוא תקף:
- סוקרטס הוא פילוסוף
- אפלטון הוא פילוסוף
- לכן: יש לפחות שני פילוסופים
בתחשיב הפרדיקטים הכמתים מופיעים כחלק מן המבנה הפנימי של הטענה, ובאמצעות כך ניתן כעת לנסח בו טענות שיש בהם כימות מרובה של מספר משתנים בעת ובעונה אחת. טכניקות אלו מעניקות ללוגיקה כוח להביע עובדות וקשרים שאינם ניתנים להבעה באמצעות תחשיב הפסוקים או בלוגיקה האריסטוטלית. למשל הוא מאפשר לתת תיאור מדויק של מושג האינסוף או למושג הגבול באנליזה המתימטית של פונקציות, שכן לשם הבעת מושגים אלו יש צורך בטענה מרובת כמתים מן הצורה "לכל ε קיים δ כך ש...". דוגמה פשוטה יחסית לאופן בו נעשה שימוש כזה בכמתים היא ההצרנה של הטענה "לכל אחד יש חבר", כאשר נציין את היחס בין חברים שוב כפרדיקט דו-מקומי, F:
בתחשיב הפרדיקטים נעשה גם שימוש בכל הקשרים הלוגיים הסטנדרטיים המוכרים מתחשיב הפסוקים (או בחלק מהם, ובלבד שתיווצר קבוצה שלמה של קשרים באמצעותה ניתן להביע כל פעולה בוליאנית):
תחביר של תחשיב הפרדיקטים
[עריכת קוד מקור | עריכה]הסמלים של תחשיב הפרדיקטים מציינים משתנים (מצויינים באותיות x,y,z עם או בלי אינדקס ממוספר), קבועים (שמות, המצויינים באותיות a,b,c וכו') ופרדיקטים (מצויינים באותיות גדולות Px, Rxy, וכו'), וכן קבועים לוגים (הקשרים והכמתים) וסימני פיסוק (סוגריים). לעתים כוללים את יחס הזהות בסימני התחשיב וכך נעשה להלן.
את הנוסחאות הבנויות היטב של התחשיב ניתן להגדיר באינדוקציה ע"פ חמשת הכללים הבאים:
- אם P הוא פרדיקט המקבל n ארגומנטים, (P(t1,...,tn היא נוסחה בנויה היטב
- אם t1 ו-t2 הם שמות או משתנים, אז t1 = t2 היא נוסחה בנויה היטב
- אם φ נוסחה בנויה היטב, אזי φ היא נוסחה בנויה היטב
- אם φ ו-ψ נוסחאות בנויות היטב, אז לכל קשר כך ש , הרי ש (ψφ) היא נוסחה בנויה היטב (דהיינו עבור כל שני פסוקים אטומים, הצבתו של אחד מן הקשרים הבינריים ביניהם יוצרת נוסחה בנויה היטב).
- אם φ היא נוסחה ו-x הוא משתנה, φ ו- φ הם נוסחאות בנויות היטב
תפקידם של הסוגריים למנוע דו-משמעות בקריאה של המשפטים. עם זאת מקובל להשמיט את הסוגריים החיצוניים ביותר. כאשר בנוסחה כל המשתנים הם קשורים, דהיינו כאשר כל משתנה מצוי בטווח של כמת מתאים, הנוסחה נחשבת כפסוק (או טענה). או אז ניתן ליחס לה ערך אמת, בהתבסס על ערך האמת של הפסוקים האטומים, כלומר בתלות בפירוש שהסמנטיקה נותנת לפרדיקטים ולתחום האובייקטים (ר' להלן).
דוגמאות
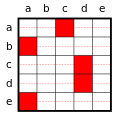
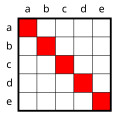
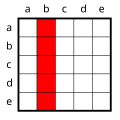
[עריכת קוד מקור | עריכה]כדוגמה נבחן את עשר הנוסחאות שניתן ליצור מן היחס "אוהב את" או לחילופין "נאהב על ידי", המקבל שני ארגומנטים, בצירופים שונים של שני הכמתים. בתור סמנטיקה נניח שמדובר בעולם בעל חמישה אובייקטים, a,b,c,d,e, ונראה אילו פירושים שונים יכולים להינתן בעולם כזה עבור היחס "אוהב את", וכיצד הטענה המכומתת יכולה לבטא פירושים אלו.
|
|
|
 | ||||||||||||
| |||||||||||||||
סמנטיקה של תחשיב הפרדיקטים
[עריכת קוד מקור | עריכה]פירוש של שפה מסדר ראשון, כמו תחשיב הפרדיקטים, מעניק מובן לכל אחד מן הקבועים הלא לוגים (השמות והפרדיקטים) וקובע את תחום-הדיון אשר על פיו נקבע הטווח של הכמתים. תכלית הפירוש היא כי לכל פסוק יינתן ערך אמת. לדוגמה:
- תחום הדיון D הוא קבוצת האובייקטים {דני, רני, יוני}
- השמות a ו-b מייצגים את דני ורני בהתאמה
- הפרדיקט החד-מקומי "חכם" מצויין על ידי P, ומקבל ערך אמת עבור האובייקטים {דני, רני}
- הפרדיקט הדו-מקומי "חבר של" מצויין על ידי R והקבוצה של האובייקטים המשוייכת אליו היא הקבוצה הריקה {}.
כעת ניתן להעריך את ערך האמת של הפסוקים הבאים בפירוש הנ"ל:
- (אמת)
- שהוא שקול ל: (אמת)
- (אמת)