משפט חוצה הזווית
ערך מחפש מקורות
| ||
| ערך מחפש מקורות | |
בגאומטריה, משפט חוצה הזווית קובע שחוצה זווית במשולש (זווית פנימית או זווית חיצונית), מחלק את הצלע בה הוא פוגע (או המשכה) ביחס שווה ליחס בין שוקי הזווית.
למשל, בתמונה שבצד, AD חוצה את זווית וחותך את BC ב-D, ולכן,
המשפט מכליל את הטענה שחוצה זווית במשולש שווה-שוקיים הוא תיכון.
המשפט ההפוך נכון גם הוא: אם ישר יוצא מקודקוד של משולש לעבר הצלע ממול ומחלק אותה ביחס שווה ליחס בין הצלעות, אז אותו ישר הוא חוצה זווית.
הוכחת המשפט
[עריכת קוד מקור | עריכה]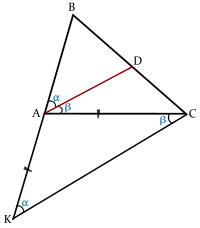
נסמן באותיות יווניות את שני חלקי הזווית החצויה: ב- את החלק הקרוב לישר AB וב- את החלק הקרוב לישר AC.
נסמן נקודה K על AB (או על המשכה), כך ש-
נקבל, על פי משפט תאלס,
מכיוון ש-, נקבל (כי זוויות מתאימות בין מקבילים שוות זו לזו) וגם (כי זוויות מתחלפות בין מקבילים שוות זו לזו)
מכיוון ש- (כי AD חוצה זווית), נקבל, על פי כלל המעבר,
מכיוון שבמשולש, מול זוויות שוות נמצאות צלעות שוות, AK=AC
נציב תוצאה זו, ונקבל
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- משפט חוצה הזווית, באתר MathWorld (באנגלית)











