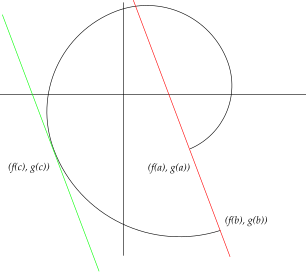
 המחשה גאומטרית של משפט הערך הממוצע של קושי: קיים משיק למסילה
המחשה גאומטרית של משפט הערך הממוצע של קושי: קיים משיק למסילה  שמקביל לישר המחבר את
שמקביל לישר המחבר את  עם
עם  .
.
בחשבון אינפיניטסימלי, משפט הערך הממוצע של קושי הוא הכללה של משפט הערך הממוצע של לגראנז' עבור זוג פונקציות. למשפט מספר שימושים מועילים, דוגמת הוכחת כלל לופיטל.
תהיינה  ו-
ו- פונקציות רציפות בקטע
פונקציות רציפות בקטע ![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa) וגזירות בקטע
וגזירות בקטע  . נניח שהנגזרת של
. נניח שהנגזרת של  לכל
לכל  . אזי קיימת נקודה
. אזי קיימת נקודה  כך שמתקיים
כך שמתקיים  .
.
הערה: מכך שהנגזרת אינה מתאפסת בקטע  ומקונטרה פוזיטיב למשפט רול מתקבל
ומקונטרה פוזיטיב למשפט רול מתקבל  ולכן אין חלוקה באפס.
ולכן אין חלוקה באפס.
משפט הערך הממוצע של לגראנז' הוא מקרה פרטי של משפט הערך הממוצע של קושי, עבור  .
.
ראשית נשים לב כי אם  אז על פי משפט רול קיימת נקודה
אז על פי משפט רול קיימת נקודה  כך ש-
כך ש- , וזאת בסתירה להנחה. לכן בהכרח
, וזאת בסתירה להנחה. לכן בהכרח  .
.
כעת נגדיר פונקציה חדשה:  פונקציה זו נבנית מהפונקציות
פונקציה זו נבנית מהפונקציות  באמצעות פעולות אלמנטריות של חיבור, חיסור, וכפל, ולכן, כמו
באמצעות פעולות אלמנטריות של חיבור, חיסור, וכפל, ולכן, כמו  , היא רציפה בקטע
, היא רציפה בקטע ![{\displaystyle \ [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c40bbeaa2f59e60b6259cebe2479bc24396f0) וגזירה בקטע
וגזירה בקטע  .
.
אם נציב, נקבל את השוויון  . לכן F מקיימת את תנאי משפט רול, ומכאן שקיימת נקודה
. לכן F מקיימת את תנאי משפט רול, ומכאן שקיימת נקודה  כך ש-
כך ש- .
.
אבל  . ולכן:
. ולכן:  .
.
על פי הנתון,  ולכן ניתן לחלק, ולקבל
ולכן ניתן לחלק, ולקבל  , כמבוקש.
, כמבוקש.







![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)













![{\displaystyle \ [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c40bbeaa2f59e60b6259cebe2479bc24396f0)







