מקדם אריזה אטומית

בקריסטלוגרפיה, מקדם אריזה אטומית (באנגלית: Atomic Packing Factor; בראשי תיבות: APF) או שבר אריזה (באנגלית: Packing Fraction) הוא החלק בנפח של מבנה גבישי הממולא באטומים. ערכו של ה־APF תמיד קטן מ-1 והוא חסר-ממדים פיזיקליים משום שהוא יחס בין נפחים.

באופן מעשי, APF נקבע על פי ההנחה שהאטומים הם מעין כדורים נוקשים. הרדיוס של כדורים אלה מקבל ערך מקסימלי באופן כזה שהאטומים אינם חופפים זה לזה. בגבישים בעלי רכיב יחיד (גבישים המכילים רק סוג אחד של אטומים), ניתן לחשב את ה־APF מתמטית באמצעות הנוסחה:

$\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {unit\_cell} }}}$

כאשר $N_{\mathrm {atoms} }$, הוא מספר האטומים בתא יחידה, $V_{\mathrm {atom} }$ הוא הנפח של האטום ו־$V_{\mathrm {unit\_cell} }$ הוא נפח תא היחידה. הוכח באופן מתמטי שבמבנים בעלי רכיב יחיד, לסידור הצפוף ביותר של אטומים יש APF של 0.74 בקירוב. במציאות, מספר זה יכול להיות גבוה יותר בשל גורמים בין-מולקולריים ספציפיים. במבנים מרובי-רכיבים, APF יכול להיות גדול מ-0.74.

מבנים חד-רכיביים

במערכת הגבישית הקובייתית

ערך מורחב – המערכת הגבישית הקובייתית

קובייתי פשוט

תא יחידה קובייתי פשוט

עבור מארז קובייתי פשוט, מספר האטומים לתא יחידה הוא 1. אורך מקצוע תא היחידה הוא $2r$, כאשר $r$ הוא רדיוס אטום.

${\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {1\cdot {\frac {4}{3}}\pi r^{3}}{\left(2r\right)^{3}}}\\[10pt]&={\frac {\pi }{6}}\approx 0.5236\end{aligned}}$

קובייתי ממורכז פאה (FCC)

מבנה FCC

עבור תא יחידה קובייתי ממורכז פאה, מספר האטומים הוא 4. ניתן למתוח קו בין הפינה העליונה של הקובייה באופן אלכסוני לבין הפינה התחתונה שממולה, שאורכו הוא $4r$. באמצעות משפט פיתגורס ניתן לבטא את $a$ כך:

$a=2{\sqrt {2}}\ r$

באמצעות נוסחה זו והנוסחה לנפח כדור, ניתן לחשב את ה־APF כך:

${\begin{aligned}\mathrm {APF} &={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\text{unit cell}}}}={\frac {4\cdot {\frac {4}{3}}\pi r^{3}}{\left(2{\sqrt {2}}\ r\right)^{3}}}\\[10pt]&={\frac {\pi {\sqrt {2}}}{6}}\approx 0.74048\end{aligned}}$

קובייתי ממרוכז גוף (BCC)

מבנה BCC

תא היחידה הפרימיטיבי עבור מבנה גבישי קובייתי ממרוכז גוף (BCC) כולל כמה מקטעים שמקורם בכמה אטומים – אטום אחד בכל פינה של הקובייה ואטום נוסף במרכזה. מאחר שנפחו של כל אטום פינה משותף ל־8 תאי יחידה, הרי שכל תא BCC מכיל שני אטומים. כל אטום פינה נוגע באטום המרכזי. בשרטוט קו העובר מפינה אחת של הקובייה דרך מרכזה ועד לפינה האחרת, יעשה הקו דרך של $4r$, כאשר $r$ הוא רדיוס האטום. בהתבסס על הגאומטריה, אורך האלכסון הוא $a{\sqrt {3}}$, ועל כן אורך כל פאה במבנה BCC זה תלוי ברדיוס האטום, לפי הנוסחה להלן:

$a={\frac {4r}{\sqrt {3}}}$

מנוסחה זאת ומהנוסחה לנפח כדור ($V=4\pi r^{3}/3$), ניתן לחשב את APF באמצעות הנוסחה:

$\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {crystal} }}}={\frac {2(4/3)\pi r^{3}}{(4r/{\sqrt {3}})^{3}}}$

$={\frac {\pi {\sqrt {3}}}{8}}\approx 0.68\,\!$

מארז הקסגונלי צפוף (HCP)

מבנה HCP

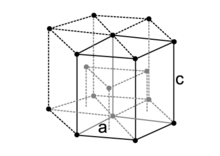
במבנה הקסגונלי (Hexagonal, שישָּני) צפוף צורת החישוב דומה. אורך כל צלע צדדית של ההקסגון הוא גובה ההקסגון, ויסומן באות $C$. מאחר שקיים:

$a=2r$

נקבל:

$c={\sqrt {\frac {2}{3}}}(4r)$

כעת ניתן לחשב את APF באמצעות הנוסחה:

$\mathrm {APF} ={\frac {N_{\mathrm {atoms} }V_{\mathrm {atom} }}{V_{\mathrm {crystal} }}}={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2](a^{2})(c)}}$

$={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2](2r)^{2}({\sqrt {\frac {2}{3}}})(4r)}}={\frac {6(4/3)\pi r^{3}}{[(3{\sqrt {3}})/2]({\sqrt {\frac {2}{3}}})(16r^{3})}}$

$={\frac {\pi }{\sqrt {18}}}\approx 0.74$

APF במבנים נפוצים

בעזרת הליכים דומים, ניתן למצוא את מקדמי האריזה האטומית האידיאליים של מבנים גבישיים שונים. אלה הנפוצים נאספו כאן בתור ערכי ייחוס, כשהם מעוגלים למאית הקרובה ביותר.

• 0.52 – מבנה קובייתי פשוט
• 0.68 – מבנה קובייתי ממרוכז גוף
• 0.74 – מבנה הקסגונלי צפוף
• 0.74 – מבנה קובייתי ממרוכז פאה
• 0.34 – מבנה קובייתי דמוי יהלום

ראו גם

• גביש

לקריאה נוספת

• Schaffer, Saxena, Antolovich, Sanders, and Warner (1999). The Science and Design of Engineering Materials (Second ed.). New York: WCB/McGraw-Hill. pp. 81–88.{{cite book}}: תחזוקה - ציטוט: multiple names: authors list (link)
• Callister, W. (2002). Materials Science and Engineering (Sixth ed.). San Francisco: John Wiley and Sons. pp. 105–114.