מספר קוונטי
מספר קוונטי (Quantum number) הוא ערך מספרי המתאר כמות נשמרת של גודל פיזיקלי בדינמיקה של מערכת קוונטית – מערכת של חלקיקים קוונטיים, אחד או יותר.
היבט חשוב של הפיזיקה הקוונטית הוא הקוונטיזציה של כמויות נצפות, הנובעת מכך שמספרים קוונטיים הם קבוצות בנות מנייה של סט דיסקרטי של מספרים שלמים, חצי שלמים או שליש שלמים. הקוונטיזציה היא אחד ההבדלים החשובים בין מכניקת הקוונטים לבין המכניקה הקלאסית, בה הערכים המאפיינים את גודלי המערכת רציפים ולא בדידים. מספרים קוונטיים רבים הם גודל חסר מימד. לעומת זאת, חלק מהמספרים הקוונטיים הם ממדיים, כגון מטען חשמלי, הנמדד ביחידות של מטען יסודי, או ספין, הנמדד ביחידות של קבוע פלאנק המצומצם.
כל התהליכים הפיזיקליים מקיימים חוקי שימור: לאחר שחלקיק, או מערכת של חלקיקים, הופכים לחלקיקים אחרים, סכומם של חלק מהמספרים הקוונטיים, שאפיינו את החלקיקים הנכנסים, זהה לסכום אותם מספרים קוונטיים המאפיינים את החלקיקים היוצאים. לדוגמה, אם אלקטרון (בעל מטען חשמלי של מינוס 1) ופוזיטרון (בעל מטען חשמלי של 1) מאיינים זה את זה, סכום המטענים החשמליים של החלקיקים היוצאים מהאירוע חייב להיות 0. אכן, תוצאה שכיחה של התנגשות אלקטרון-פוזיטרון היא שני פוטונים, שמטענם החשמלי הוא 0. לעומת זאת, אפשר שמקצת המספרים הקוונטיים של החלקיקים הנכנסים יהיו שונים מאלו של החלקיקים היוצאים, כלומר, יופר חוק שימור. דוגמה לתהליך כזה היא המרה של קווארקים מסוימים לקווארקים אחרים, כפי שעושה למשל דעיכת בטא, הגורמת לכך שהאיזוספין של החלקיק היוצא יהיה שונה מזה של החלקיק הנכנס. תהליכים אלו מתווכים על ידי הכוח החלש. לפי משפט נתר, חוקי שימור קשורים לסימטריה. לכן, תהליכים המפירים חוק שימור הם דוגמה לשבירת סימטריה, כגון שבירת סימטריה ספונטנית.
עבור כל מערכת קוונטית, קיים מספר קוונטי אחד או יותר המתאר אותה. לכן, קשה למנות את כל המספרים הקוונטיים האפשריים. המספרים הקוונטיים נחלקים לשתי משפחות עיקריות. הראשונה היא מספרים קוונטיים כלליים, העשויים לתאר כל חלקיק קוונטי. רבים מאלו הם מספרים קוונטיים של טעם (flavor quantum numbers), הקובעים את סוג החלקיק. השימוש במספרים אלו נפוץ בתחום פיזיקת החלקיקים. המשפחה השנייה היא מספרים קוונטיים אלקטרוניים, המתארים את רמות האנרגיה של אלקטרונים באטומים. מספרים אלו מוגדרים כ"סט של ערכים מספריים אשר נותנים פתרונות מקובלים של משוואת הגלים של שרדינגר עבור אטום המימן". השימוש במספרים אלו נפוץ בתחום פיזיקת הקוונטים.
מספרים קוונטיים כלליים
[עריכת קוד מקור | עריכה]מטען חשמלי
[עריכת קוד מקור | עריכה] ערך מורחב – מטען חשמלי
ערך מורחב – מטען חשמלי
מטען חשמלי הוא מספר קוונטי הקובע את אופן ההתנהגות של חלקיקים תחת השפעת הכוח האלקטרומגנטי. מטען חשמלי מסומן Q. מושג המטען החשמלי היה מוכר זמן רב לפני פיתוח התאוריה הקוונטית. למעשה, המטען החשמלי הוא אחת התופעות החשובות ביותר בפיזיקה הקלאסית. בה בעת, הוא מאפיין מרכזי של מערכות קוונטיות – אלו מביניהן הטעונות חשמלית. החלקיקים הידועים ביותר, הנושאים מספר קוונטי זה, הם הפרוטון והאלקטרון, בעלי מטענים חשמליים של 1 ומינוס 1, בהתאמה.
קווארקים נושאים מטען חשמלי שאינו מספר שלם, אלא כפולה של 1⁄3. הקווארקים למעלה, קסום ועליון הם בעלי מטען חשמלי של 2⁄3, בעוד הקווארקים למטה, מוזר ותחתון הם בעלי מטען חשמלי של מינוס 1⁄3. האנטיקווארקים של כל אחד מאלו נושאים את המטען החשמלי הנגדי. קווארקים תמיד מחוברים לכדי חלקיקים מורכבים, האדרונים, שהמטען החשמלי שלהם הוא תמיד מספר שלם. כך, לדוגמה, שני קווארקי למעלה ועוד קווארק למטה מרכיבים את הפרוטון, שמטענו החשמלי 1 (דהיינו, 2⁄3 ועוד 2⁄3 מינוס 1⁄3). שני קווארקי למטה ועוד קווארק למעלה מרכיבים את הנייטרון, שמטענו החשמלי 0 (דהיינו, מינוס 1⁄3 מינוס 1⁄3 ועוד 2⁄3). שני קווארקי אנטי-למעלה ועוד קווארק אנטי-למטה מרכיבים את האנטיפרוטון, שמטענו החשמלי מינוס 1 (דהיינו, מינוס 2⁄3 מינוס 2⁄3 ועוד 1⁄3). קווארק למעלה וקווארק אנטי-למטה מרכיבים את הפאיון החיובי, שמטענו החשמלי 1; האנטי-חלקיקים שלהם מרכיבים את הפאיון השלילי; קווארק למעלה וקווארק אנטי-למעלה, או קווארק למטה וקווארק אנטי-למטה, מרכיבים את הפאיון הנייטרלי.
הפוטון נושא את הכוח האלקטרומגנטי, הפועל בין חלקיקים בעלי מטען חשמלי. לפוטון עצמו יש מטען חשמלי של 0.
לפי חוק שימור המטען החשמלי, שהוא דוגמה לשימור מדויק (exact conservation), המטען החשמלי הוא מספר קוונטי הנשמר תמיד, כלומר, אף תהליך פיזיקלי מוכר אינו משנה את סכום המטענים החשמליים משני צדי התהליך.
ספין
[עריכת קוד מקור | עריכה] ערך מורחב – ספין (פיזיקה)
ערך מורחב – ספין (פיזיקה)
ספין או תנע זוויתי פנימי (spin או intrinsic angular momentum), המסומן s, הוא מספר קוונטי המתאר ערך עצמי של אופרטור תנע זוויתי פנימי, S, באופן הבא:
הספין של חלקיק קובע האם החלקיק הוא בוזון או פרמיון. כאשר הספין הוא מספר שלם, החלקיק הוא בוזון. כאשר הספין הוא מספר חצי שלם, החלקיק הוא פרמיון. פרמיונים מצייתים לעקרון האיסור של פאולי, הקובע ששני פרמיונים אינם יכולים להימצא באותו מצב קוונטי בו זמנית.
ספין אינו מספר קוונטי חיבורי (additive quantum number), כלומר, הספין הוא תמיד חיובי או אפס. כתוצאה מכך, סכום הספינים לפני ואחרי תהליך פיזיקלי אינו בהכרח שווה.
מספר באריוני
[עריכת קוד מקור | עריכה] ערך מורחב – מספר באריוני
ערך מורחב – מספר באריוני
מספר באריוני (baryon number) הוא מספר קוונטי המתאר את שליש ההפרש בין כמות הקווארקים לכמות האנטיקווארקים המצויים בחלקיק. מספר באריוני מסומן B.
המספר הבאריוני של כל באריון הוא 1, בעוד המספר הבאריוני של כל אנטי-באריון הוא מינוס 1. לדוגמה, לפרוטון ולנייטרון יש מספר באריוני של 1, בעוד לאנטיפרוטון ולאנטינייטרון יש מספר באריוני של מינוס 1. לכל קווארק יש מספר באריוני של 1⁄3. לכל אנטיקווארק יש מספר באריוני של מינוס 1⁄3. לחלקיקים שאינם באריונים או קווארקים יש מספר באריוני של 0. בהתאם, למזונים – האדרונים המורכבים מקווארק ואנטיקווארק – יש מספר באריוני של 0, זאת ולו מהסיבה הפשוטה שהמספר הבאריוני של הקווארק מבטל את המספר הבאריוני של האנטיקווארק.
בתחום ההאדרונים האקזוטיים, חישוב המספר הבאריוני מאפשר להבחין בין באריונים אקזוטיים, להם מספר באריוני של 1, למזונים אקזוטיים, להם מספר באריוני של 0.
מספר לפטוני
[עריכת קוד מקור | עריכה]מספר לפטוני (lepton number) הוא מספר קוונטי המתאר את ההפרש בין כמות הלפטונים לכמות האנטילפטונים המצויים בחלקיק. מספר לפטוני מסומן L.
לאלקטרון, למואון ולטאו יש מספר לפטוני של 1. לאנטי-חלקיקים שלהם – פוזיטרון, אנטימואון ואנטיטאו – יש מספר לפטוני של מינוס 1. לניוטרינו יש מספר לפטוני של 1, בעוד לאנטיניוטרינו יש מספר לפטוני של מינוס 1. לחלקיקים שאינם לפטוניים יש מספר לפטוני של 0.
בדעיכת בטא מינוס או פלוס, נפלט יחד עם האלקטרון או הפוזיטרון גם אנטיניוטרינו או ניוטרינו, בהתאמה. הסיבה לכך היא שדעיכת בטא משמרת את המספר הלפטוני. סכום המספרים הלפטוניים של האנטיניוטרינו והאלקטרון, או של הניוטרינו והפוזיטרון, הוא 0, בדיוק כמו המספר הלפטוני של החלקיק הנכנס, שהוא נייטרון או פרוטון.
איזוספין חלש
[עריכת קוד מקור | עריכה]איזוספין חלש (weak isospin) הוא מספר קוונטי הקובע את אופן ההתנהגות של חלקיקים תחת השפעת הכוח החלש. ניתן לתאר את האיזוספין החלש כ"מטען הכוח החלש" של חלקיק. הדיון על האיזוספין החלש להלן מתייחס לרכיב השלישי של האיזוספין החלש (third component of weak isospin), המסומן T3.
מבין הבוזונים הנושאים את הכוח החלש, האיזוספין החלש של בוזון W+ הוא 1, של בוזון W- הוא מינוס 1 ושל בוזון Z הוא 0. לכל הפרמיונים היסודיים יש איזוספין חלש של 1⁄2 או מינוס 1⁄2. לגבי קווארקי למעלה ולמטה, הרכיב השלישי של האיזוספין שווה לאיזוספין החלש, כלומר I3=T3. לקווארקים שמטענם החשמלי חיובי (למעלה, קסום, עליון) יש איזוספין חלש של 1⁄2. לקווארקים שמטענם החשמלי שלילי (למטה, מוזר, תחתון) יש איזוספין חלש של מינוס 1⁄2. ללפטונים הטעונים שלילית יש איזוספין חלש של מינוס 1⁄2. ללפטונים הנייטרליים, כלומר, חלקיקי ניוטרינו, יש איזוספין חלש של 1⁄2. לאנטי-חלקיקים של כל אחד מאלו יש את הערך הנגדי.
כל ערכי האיזוספין החלש הנזכרים לעיל מתייחסים לחלקיקים בעלי כיראליות שמאלית, או ימנית עבור אנטי-חלקיקים. האיזוספין החלש חווה שבירת סימטריה כיראלית בין שמאלית (left-handed chirality) לימנית (right-handed chirality). תחת כיראליות ימנית, או שמאלית עבור אנטי-חלקיקים, האיזוספין החלש הוא 0. פרמיונים עם כיראליות ימנית, כמו אנטיפרמיונים עם כיראליות שמאלית, אינם משתתפים בתהליכים של הכוח החלש.
לחלקיקים שאינם יסודיים, כלומר, האדרונים, אין כלל ערך של איזוספין חלש. זאת, מכיוון שהאדרונים הם תוצאה של תהליך של הכוח החזק, שאינו משמר את האיזוספין החלש.
היפרמטען חלש
[עריכת קוד מקור | עריכה]היפרמטען חלש (weak hypercharge) הוא מספר קוונטי המקשר בין המטען החשמלי, Q, לבין האיזוספין החלש, T3, של חלקיק. ההיפרמטען החלש הוא המספר הקוונטי המאפיין את הכוח האלקטרו-חלש. הוא קשור לסימטריית הכיול U(1). היפרמטען חלש מסומן YW.
ההיפרמטען החלש מתאר סימטריה שהתקיימה בעידן האלקטרו-חלש, השלב של המפץ הגדול שלאחר ההיפרדות בין הלפטונים לקווארקים, אך טרם הפיצול של הלפטונים והקווארקים לטעמים ולדורות שונים. לכן, לכל הלפטונים יש ערך זהה של היפרמטען חלש, מינוס 1; לכל האנטילפטונים יש היפרמטען חלש של 1; לכל הקווארקים יש היפרמטען חלש של 1⁄3 ולכל האנטיקווארקים יש היפרמטען חלש של מינוס 1⁄3. לגבי קווארקים, ההיפרמטען החלש שווה למספר הבאריוני. לגבי לפטונים, ההיפרמטען החלש נגדי למספר הלפטוני. נתונים אלו מתייחסים לחלקיקים בעלי כיראליות שמאלית ולאנטי-חלקיקים בעלי כיראליות ימנית.
כדי שלחלקיק יהיה ערך של היפרמטען חלש, נדרש שיהיה לו ערך של איזוספין חלש – ולהפך. על כן, נתון זה קיים רק עבור חלקיקים יסודיים. להאדרונים אין כלל ערך של היפרמטען חלש.
איזוספין
[עריכת קוד מקור | עריכה]איזוספין (isospin) הוא מספר קוונטי המתאר את כמות קווארקי למעלה וקווארקי למטה, או האנטיקווארקים שלהם, המצויים בחלקיק. הרכיב השלישי של האיזוספין, המתואר להלן, נקבע לפי הנוסחה:
האיזוספין כשלעצמו, המסומן I, נושא ערך שיכול להיות רק חיובי או אפס. כך, לדוגמה, הן לקווארק למעלה והן לקווארק למטה יש איזוספין של 1⁄2. נתון משמעותי יותר הוא הרכיב השלישי של האיזוספין (third component of isospin), המסומן I3 או Iz ומהווה השלכה (projection) של האיזוספין, המאפשרת ערך חיובי, שלילי או אפסי. כך, לדוגמה, לקווארק למעלה יש I3 של 1⁄2, לקווארק למטה יש I3 של מינוס 1⁄2, לפרוטון יש I3 של 1⁄2, לנייטרון יש I3 של מינוס 1⁄2, לפאיון החיובי יש I3 של 1, לפאיון השלילי יש I3 של מינוס 1 ולפאיון הנייטרלי יש I3 של 0.
ניתן לראות את המספר הקוונטי I3 כמשלב לתוכו את המספר למעליות (upness) ואת המספר למטיות (downness), שאינם מוכרים כמספרים קוונטיים כשלעצמם, בניגוד למוזרות, קסם, תחתיות ועליוניות. הרכיב השלישי של האיזוספין הוא מחצית סכום הלמעליות והלמטיות של חלקיק.
לחלקיקים שאינם מהווים או כוללים קווארקי למעלה או למטה, או את האנטיקווארקים שלהם, יש איזוספין של 0.
קסם
[עריכת קוד מקור | עריכה]קסם (charm) הוא מספר קוונטי המתאר את ההפרש בין כמות קווארקי קסום לכמות קווארקי אנטי-קסום המצויים בחלקיק. הקסם של קווארק קסום הוא 1 ושל קווארק אנטי-קסום הוא מינוס 1. קסם מסומן C.
מוזרות
[עריכת קוד מקור | עריכה]מוזרות (strangeness) היא מספר קוונטי המתאר את ההפרש בין כמות קווארקי אנטי-מוזר לכמות קווארקי מוזר המצויים בחלקיק. המוזרות של קווארק מוזר היא מינוס 1 ושל קווארק אנטי-מוזר היא 1. מוזרות מסומנת S.
עליוניות
[עריכת קוד מקור | עריכה]עליוניות (topness) היא מספר קוונטי המתאר את ההפרש בין כמות קווארקי עליון לכמות קווארקי אנטי-עליון המצויים בחלקיק. העליוניות של קווארק עליון היא 1 ושל קווארק אנטי-עליון היא מינוס 1. עליוניות מסומנת T.
קווארקי עליון אינם עוברים תהליך של האדרוניזציה (hadronization), עקב אורך החיים הקצר שלהם, כך שהם אינם יכולים להוות מרכיב של חלקיקים מורכבים כלשהם אותם המספר עליוניות יהיה עשוי לתאר. על כן, העליוניות של כל ההאדרונים היא 0.
תחתיות
[עריכת קוד מקור | עריכה]תחתיות (bottomness) היא מספר קוונטי המתאר את ההפרש בין כמות קווארקי אנטי-תחתון לכמות קווארקי תחתון המצויים בחלקיק. התחתיות של קווארק תחתון היא מינוס 1 ושל קווארק אנטי-תחתון היא 1. תחתיות מסומנת B'.
היפרמטען
[עריכת קוד מקור | עריכה]היפרמטען (hypercharge) הוא מספר קוונטי המשלב את המספרים הקוונטיים של הטעם הקשורים לכוח החזק. היפרמטען מסומן Y.
כך, לדוגמה, לפרוטון ולנייטרון יש היפרמטען של 1, מכיוון שמספר הבאריון שלהם הוא 1 ואילו מספרי הקסם, מוזרות, עליוניות ותחתיות שלהם הם 0.
ההיפרמטען אינו נשמר תמיד. תהליכים של הכוח החלש עשויים להפר אותו, אם כי הוא נשמר בחלק מהם, לרבות דעיכת בטא.
נוסחת גל-מן-נישיג'ימה (Gell-Mann–Nishijima formula) מקשרת בין היפרמטען, איזוספין ומטען חשמלי של קווארקים והאדרונים:
טבלת מספרים קוונטיים של חלקיקים
[עריכת קוד מקור | עריכה]הטבלה להלן מפרטת חלק מהמספרים הקוונטיים של חלקיקים אחדים, לרבות כל החלקיקים היסודיים.
| חלקיק | סמל | Q | s | B | L | T3 | YW | I3 | C | S | T | B' | Y | קווארקי ערכיות |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| פוטון | γ | 0 | 1 | 0 | 0 | 0, 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| גלואון | g | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| בוזון W+ | W+ | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| בוזון W- | W- | -1 | 1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| בוזון Z | Z0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| בוזון היגס | H0 | 0 | 0 | 0 | 0 | -1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אלקטרון | e- | -1 | 1⁄2 | 0 | 1 | -1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטיאלקטרון / פוזיטרון | e+ | 1 | 1⁄2 | 0 | -1 | 1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ניוטרינו אלקטרוני | νe | 0 | 1⁄2 | 0 | 1 | 1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטיניוטרינו אלקטרוני | νe | 0 | 1⁄2 | 0 | -1 | -1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| מואון | μ- | -1 | 1⁄2 | 0 | 1 | -1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטימואון | μ+ | 1 | 1⁄2 | 0 | -1 | 1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ניוטרינו מואוני | νμ | 0 | 1⁄2 | 0 | 1 | 1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטיניוטרינו מואוני | νμ | 0 | 1⁄2 | 0 | -1 | -1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| טאו | τ- | -1 | 1⁄2 | 0 | 1 | -1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטיטאו | τ+ | 1 | 1⁄2 | 0 | -1 | 1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| ניוטרינו טאואוני | ντ | 0 | 1⁄2 | 0 | 1 | 1⁄2 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| אנטיניוטרינו טאואוני | ντ | 0 | 1⁄2 | 0 | -1 | -1⁄2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| קווארק למעלה | u | 2⁄3 | 1⁄2 | 1⁄3 | 0 | 1⁄2 | 1⁄3 | 1⁄2 | 0 | 0 | 0 | 0 | 1⁄3 | |
| אנטיקווארק למעלה | u | -2⁄3 | 1⁄2 | -1⁄3 | 0 | -1⁄2 | -1⁄3 | -1⁄2 | 0 | 0 | 0 | 0 | -1⁄3 | |
| קווארק למטה | d | -1⁄3 | 1⁄2 | 1⁄3 | 0 | -1⁄2 | 1⁄3 | -1⁄2 | 0 | 0 | 0 | 0 | 1⁄3 | |
| אנטיקווארק למטה | d | 1⁄3 | 1⁄2 | -1⁄3 | 0 | 1⁄2 | -1⁄3 | 1⁄2 | 0 | 0 | 0 | 0 | -1⁄3 | |
| קווארק קסום | c | 2⁄3 | 1⁄2 | 1⁄3 | 0 | 1⁄2 | 1⁄3 | 0 | 1 | 0 | 0 | 0 | 4⁄3 | |
| אנטיקווארק קסום | c | -2⁄3 | 1⁄2 | -1⁄3 | 0 | -1⁄2 | -1⁄3 | 0 | -1 | 0 | 0 | 0 | -4⁄3 | |
| קווארק מוזר | s | -1⁄3 | 1⁄2 | 1⁄3 | 0 | -1⁄2 | 1⁄3 | 0 | 0 | -1 | 0 | 0 | -2⁄3 | |
| אנטיקווארק מוזר | s | 1⁄3 | 1⁄2 | -1⁄3 | 0 | 1⁄2 | -1⁄3 | 0 | 0 | 1 | 0 | 0 | 2⁄3 | |
| קווארק עליון | t | 2⁄3 | 1⁄2 | 1⁄3 | 0 | 1⁄2 | 1⁄3 | 0 | 0 | 0 | 1 | 0 | 4⁄3 | |
| אנטיקווארק עליון | t | -2⁄3 | 1⁄2 | -1⁄3 | 0 | -1⁄2 | -1⁄3 | 0 | 0 | 0 | -1 | 0 | -4⁄3 | |
| קווארק תחתון | b | -1⁄3 | 1⁄2 | 1⁄3 | 0 | -1⁄2 | 1⁄3 | 0 | 0 | 0 | 0 | -1 | -2⁄3 | |
| אנטיקווארק תחתון | b | 1⁄3 | 1⁄2 | -1⁄3 | 0 | 1⁄2 | -1⁄3 | 0 | 0 | 0 | 0 | 1 | 2⁄3 | |
| פרוטון | p | 1 | 1⁄2 | 1 | 0 | – | – | 1⁄2 | 0 | 0 | 0 | 0 | 1 | uud |
| אנטיפרוטון | p | -1 | 1⁄2 | -1 | 0 | – | – | -1⁄2 | 0 | 0 | 0 | 0 | -1 | uud |
| נייטרון | n | 0 | 1⁄2 | 1 | 0 | – | – | -1⁄2 | 0 | 0 | 0 | 0 | 1 | udd |
| אנטינייטרון | n | 0 | 1⁄2 | -1 | 0 | – | – | 1⁄2 | 0 | 0 | 0 | 0 | -1 | udd |
| פאיון / פאיון חיובי | π+ | 1 | 0 | 0 | 0 | – | – | 1 | 0 | 0 | 0 | 0 | 0 | ud |
| אנטיפאיון / פאיון שלילי | π- | -1 | 0 | 0 | 0 | – | – | -1 | 0 | 0 | 0 | 0 | 0 | du |
| פאיון נייטרלי | π0 | 0 | 0 | 0 | 0 | – | – | 0 | 0 | 0 | 0 | 0 | 0 | uu - dd2√ |
| אטא | η0 | 0 | 0 | 0 | 0 | – | – | 0 | 0 | 0 | 0 | 0 | 0 | uu + dd - 2ss6√ |
| מזון D / מזון D חיובי | D+ | 1 | 0 | 0 | 0 | – | – | 1⁄2 | 1 | 0 | 0 | 0 | 1 | cd |
| אנטימזון D / מזון D שלילי | D- | -1 | 0 | 0 | 0 | – | – | -1⁄2 | -1 | 0 | 0 | 0 | -1 | dc |
| מזון D נייטרלי | D0 | 0 | 0 | 0 | 0 | – | – | -1⁄2 | 1 | 0 | 0 | 0 | 1 | cu |
| אנטימזון D נייטרלי | D0 | 0 | 0 | 0 | 0 | – | – | 1⁄2 | -1 | 0 | 0 | 0 | -1 | uc |
| קאון / קאון חיובי | K+ | 1 | 0 | 0 | 0 | – | – | 1⁄2 | 0 | 1 | 0 | 0 | 1 | us |
| אנטיקאון / קאון שלילי | K- | -1 | 0 | 0 | 0 | – | – | -1⁄2 | 0 | -1 | 0 | 0 | -1 | su |
| קאון נייטרלי | K0 | 0 | 0 | 0 | 0 | – | – | -1⁄2 | 0 | 1 | 0 | 0 | 1 | ds |
| אנטיקאון נייטרלי | K0 | 0 | 0 | 0 | 0 | – | – | 1⁄2 | 0 | -1 | 0 | 0 | -1 | sd |
| מזון B / מזון B חיובי | B+ | 1 | 0 | 0 | 0 | – | – | 1⁄2 | 0 | 0 | 0 | 1 | 1 | ub |
| אנטימזון B / מזון B שלילי | B- | -1 | 0 | 0 | 0 | – | – | -1⁄2 | 0 | 0 | 0 | -1 | -1 | bu |
| מזון B נייטרלי | B0 | 0 | 0 | 0 | 0 | – | – | -1⁄2 | 0 | 0 | 0 | 1 | 1 | db |
| אנטימזון B נייטרלי | B0 | 0 | 0 | 0 | 0 | – | – | 1⁄2 | 0 | 0 | 0 | -1 | -1 | bd |
| J/psi | J/ψ | 0 | 1 | 0 | 0 | – | – | 0 | 0 | 0 | 0 | 0 | 0 | cc |
| פי | Φ0 | 0 | 1 | 0 | 0 | – | – | 0 | 0 | 0 | 0 | 0 | 0 | ss |
| אופסילון | Υ0 | 0 | 1 | 0 | 0 | – | – | 0 | 0 | 0 | 0 | 0 | 0 | bb |
מספרים קוונטיים אלקטרוניים
[עריכת קוד מקור | עריכה]המספרים הקוונטיים האלקטרוניים הם ארבעה מספרים קוונטיים, המתארים באופן חד-חד-ערכי כל אלקטרון הקיים באטום מסוים. חלק מהמספרים הקוונטיים האלקטרוניים עשויים להיות זהים עבור שני אלקטרונים באותו אטום, אך לא ייתכן שכל הארבעה יהיו זהים. מספרים אלו מרכיבים פתרון שלם ומלא של משוואת שרדינגר עבור אטום המימן.
ארבעת המספרים הקוונטיים האלקטרוניים הם:
- מספר קוונטי יסודי (principal quantum number), שסימנו .
- מספר קוונטי זוויתי (azimuthal quantum number), שסימנו .
- מספר קוונטי מגנטי (magnetic quantum number), שסימנו או .
- מספר קוונטי ספיני שניוני (secondary spin quantum number), שסימנו .
אינטראקציית אורביטל-ספין (אנ') יוצרת יחס בין מספרים אלה. לפיכך, תיאור מלא של המערכת יכול להינתן גם עם פחות מ-4 מספרים קוונטיים, אם נעשות בחירות אורתוגונליות מתאימות עבור וקטורי הבסיס.
נומנקלטורה של אלקטרון באטום
[עריכת קוד מקור | עריכה]מודלים רבים ושונים הוצעו לאורך ההיסטוריה של מכניקת הקוואנטים, אך מערכת הנומנקלטורה החשובה ביותר נוצרה מהתאוריה האורביטלית מולקולרית של פרידריך הונד ורוברט מוליקן ומתרומותיהם של שרדינגר, סלייטר (אנ') וג'ון לנרד ג'ונס (אנ'). מערכת זו של נומנקלטורה משלבת את מודל רמות האנרגיה של בוהר, התאוריה האורביטלית של הונד-מוליקן ותצפיות על ספין האלקטרון המבוססות על ספקטרוסקופיה וכללי הונד.[1]
מודל זה מתאר קליפות אלקטרונים באמצעות ארבעה מספרים קוונטיים, כדלקמן. זהו גם המינוח המשותף בתיאור הקלאסי של קליפות חלקיקים גרעיניים (פרוטונים ונייטרונים). תיאור קוונטי של אורביטל מולקולרי דורש מספרים קוונטיים שונים, בגלל ההמילטוניאן והסימטריות השונות שלו (קשרי סיגמא, פאי, דלתא, פי).
מספר קוונטי יסודי
[עריכת קוד מקור | עריכה] ערך מורחב – מספר קוונטי יסודי
ערך מורחב – מספר קוונטי יסודי
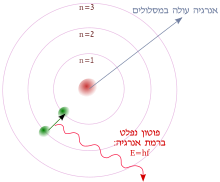
מתאר את הקליפה, או רמת האנרגיה של אלקטרון. ערכו של נע במרווחים שלמים בין 1 לבין מספרה של הקליפה החיצונית ביותר באטום אשר מכילה את אלקטרוני הערכיות:[2]

לדוגמה: עבור צסיום (Cs) אלקטרון הערכיות החיצוני ביותר נמצא ברמת אנרגיה מספר 6 ולכן אלקטרון צסיום מתואר על ידי ערכי בטווח .
עבור חלקיקים בפוטנציאל לא תלוי זמן (ראה משוואת שרדינגר), מספר זה מציין את הערך העצמי ה--י של ההמילטוניאן (H), דהיינו האנרגיה, E ללא התרומה של התנע הזוויתי ().
לכן, למספר זה יש תלות רק במרחק בין האלקטרון לבין הגרעין (הקואורדינטה הרדיאלית, r). מרחק זה גדל עם n, ולכן מצבים קוונטיים עם מספרים קוונטיים יסודיים שונים משויכים לקליפות שונות.
מספר קוונטי זוויתי
[עריכת קוד מקור | עריכה] ערך מורחב – מספר קוונטי זוויתי
ערך מורחב – מספר קוונטי זוויתי

ידוע גם כמספר קוונטי אורביטלי, מתאר תת-קליפה אלקטרונית ומבטא את הגודל של התנע הזוויתי (מסומן כאופרטור התנע הזוויתי האורביטלי ) דרך היחס הבא: בכימיה ובספקטרוסקופיה, מסומן כאורביטל , מסומן כאורביטל , מסומן כאורביטל ו - מסומן כאורביטל .
ערכי משתנים בטווח במרווחים שלמים[3] מאחר שהרמה הראשונה מכילה רק אורביטל , הרמה השנייה מכילה בנוסף ל- גם אורביטל , השלישית מכילה בנוסף ל- ו- גם אורביטל וכן הלאה:[4]
למספר זה יש חשיבות רבה בכימיה שכן הוא מגדיר את האורביטל האטומי ומשפיע על הקשר הכימי ועל זווית הקשר.
מספר קוונטי מגנטי
[עריכת קוד מקור | עריכה] ערך מורחב – מספר קוונטי מגנטי
ערך מורחב – מספר קוונטי מגנטי

מתאר אורביטל מסוים (או "ענן") בתוך תת-קליפה אלקטרונית ומבטא את היטל התנע הזוויתי של האורביטל לאורך ציר מוגדר:
ערכי משתנים בטווח במרווחים שלמים:
תת קליפת מכילה רק אורביטל אחד ולכן המספר הקוונטי המגנטי של אלקטרון ברמה זו, , תמיד יהיה שווה ל-אפס.
לעומת זאת, תת-קליפת מכילה 3 אורביטלים ולכן המספר הקוונטי המגנטי של אלקטרון ברמה זו, , יכול לקבל את אחד מ-3 הערכים:
בתת קליפה ישנם 5 אורביטלים ולכן המספר הקוונטי המגנטי של אלקטרון ברמה זו, , יכול לקבל אחד מ-5 הערכים:
מספר קוונטי ספיני שניוני
[עריכת קוד מקור | עריכה] ערך מורחב – מספר קוונטי ספיני שניוני
ערך מורחב – מספר קוונטי ספיני שניוני
מכונה גם מספר קוונטי ספיני היטלי, מתאר את , הספין (תנע זוויתי פנימי) של האלקטרון בתוך האורביטל ומבטא את היטלו לאורך ציר :
ערכי משתנים בטווח במרווחים שלמים:[5]
לאלקטרון בודד יש מספר ספין וכתוצאה מכך המספר הקוונטי הספיני השניוני שלו הוא שמשמעותו פיצול לרמות אנרגיה או למצבים עצמיים:
- ספין "מעלה" ("spin up") - מתאים לערך
- ספין "מטה" ("spin down") - מתאים לערך
עקב עיקרון האיסור של פאולי, האלקטרונים המאכלסים אורביטל יחיד חייבים להיות במצבים קוונטיים שונים זה מזה. לכן, כל אורביטל יכול להכיל רק 2 אלקטרונים (עם מצבים עצמיים שונים) לכל היותר.
כללי 4 המספרים מסוכמים בטבלה הבאה:
| שם | סימול | משמעות מרחבית | טווח הערכים | דוגמאות לערכים |
|---|---|---|---|---|
| מספר קוונטי יסודי | קליפת אלקטרונים | |||
| מספר קוונטי זוויתי | תת קליפת אלקטרונים | עבור : | ||
| מספר קוונטי מגנטי | אורביטל בודד בתוך תת קליפת אלקטרונים | עבור :
| ||
| מספר קוונטי ספיני שניוני | היטל או כיוון הספין של האלקטרונים בתוך אורביטל בודד - ספין "מעלה" או ספין "מטה" | עבור אלקטרון ולכן |
דוגמה: המספרים הקוונטיים של אלקטרוני הערכיות בשכבה החיצונית ביותר של אטום הפחמן (C), הנמצאים באורביטל , הם: - הקליפה האלקטרונית השנייה, - תת-קליפה אלקטרונית , אחת מ-3 האפשרויות: ו- - עבור ספינים מקבילים.
תוצאות ספקטרוסקופיה מראות כי אורביטל אטומי יכול לאכלס עד שני אלקטרונים. עם זאת, על פי כללי הונד, אשר כוללים בתוכם גם את עקרון האיסור של פאולי, שני אלקטרונים לא יכולים להיות באותו מצב קוונטי בדיוק ולא באותה קבוצה של מספרים קוונטיים. הנחת אד הוק הייתה כי למספר הקוונטי הרביעי יש רק שני ערכים אפשריים. הנחה זו אומתה מאוחר יותר על ידי ניסוי שטרן-גרלך ומכניקת הקוונטים היחסותית.
מספרים קוונטיים של תנע זוויתי כולל
[עריכת קוד מקור | עריכה]כאשר נלקחת בחשבון אינטראקציית אורביטל-ספין (Spin–orbit interaction), האופרטורים ו- כבר לא קומוטטיביים עם ההמילטוניאן ולכן ערכיהם העצמיים משתנים עם הזמן.
במקרה זה, מספרים קוונטיים אחרים משמשים לתיאור התנע הזוויתי:[6][7]
- מספר קוונטי זוויתי כולל (total angular momentum quantum number), שסימנו .
- היטל תנע זוויתי כולל (projection of the total angular momentum), שסימנו .
- שיקוף (parity), שסימנו
מספר קוונטי זוויתי כולל
[עריכת קוד מקור | עריכה]מבטא את הגודל של התנע הזוויתי הכולל (המסומן כאופרטור ) דרך היחס הבא:
מאחר ש- ערכי משתנים במרווחים שלמים בטווח הבא:
היטל תנע זוויתי כולל
[עריכת קוד מקור | עריכה]מבטא את היטל התנע הזוויתי הכולל לאורך ציר מוגדר:
ערכי משתנים בטווח במרווחים שלמים:
כאשר ניתן לבטא זאת באנלוגיה גם כך:
שיקוף
[עריכת קוד מקור | עריכה] ערך מורחב – סימטריית CPT
ערך מורחב – סימטריית CPT
סימטריית שיקוף (parity) מציינת את היפוך הקואורדינטות של המרחב בדומה לשיקוף במראה:
המספר הקוונטי מבטא את הערך העצמי של סימטריה זו:
כאשר:
- עבור מצבים קוונטיים שמקורם בתנע זוויתי, , זוגי, השיקוף חיובי ונקרא זוגי .
- עבור מצבים קוונטיים שמקורם בתנע זוויתי, , אי-זוגי, השיקוף שלילי ונקרא אי-זוגי .
לדוגמה:
| # | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1. | 2 | 1 | 1 | 1/2 | 1/2 | 3/2 | 3/2 | ||
| 2. | 2 | 1 | 1 | 1/2 | 1/2− | 3/2 | 1/2 | 1/2 | |
| 3. | 2 | 1 | 0 | 1/2 | 1/2 | 3/2 | 1/2 | 1/2 | |
| 4. | 2 | 1 | 0 | 1/2 | 1/2− | 3/2 | 1/2 | 1/2− | |
| 5. | 2 | 1 | 1− | 1/2 | 1/2 | 3/2 | 1/2 | 1/2− | |
| 6. | 2 | 1 | 1− | 1/2 | 1/2− | 3/2 | 3/2− | ||
| 7. | 2 | 0 | 0 | 1/2 | 1/2 | 1/2 | 1/2- | 1/2 | |
| 8. | 2 | 0 | 0 | 1/2 | 1/2− | 1/2 | 1/2- | 1/2− |
המצבים הקוונטיים במערכת זו ניתנים לתיאור כקומבינציה ליניארית של 8 המצבים שלעיל. אך, בנוכחות של אינטראקציית אורביטל-ספין, המערכת מתוארת על ידי 8 מצבים חדשים אחרים המהווים ערכים עצמיים של ההמילטוניאן ומקורם במצבים הישנים:
| # | מצבים ישנים | |||
|---|---|---|---|---|
| 1. | 3/2 | 3/2 | אי-זוגי | 1 |
| 2. | 3/2 | 1/2 | אי-זוגי | 2,3 |
| 3. | 3/2 | 1/2− | אי-זוגי | 4,5 |
| 4. | 3/2 | 3/2- | אי-זוגי | 6 |
| 5. | 1/2 | 1/2 | אי-זוגי | 2,3 |
| 6. | 1/2 | 1/2− | אי-זוגי | 4,5 |
| 7. | 1/2 | 1/2 | זוגי | 7 |
| 8. | 1/2 | 1/2− | זוגי | 8 |
ראו גם
[עריכת קוד מקור | עריכה]- פיזיקת חלקיקים
- המודל הסטנדרטי
- מכניקת הקוונטים
- משוואת שרדינגר
- קונפיגורציה אלקטרונית
- אורביטל אטומי
- רמת אנרגיה
- קליפת אלקטרונים
- מודל האטום של בוהר
- פיזיקה אטומית
לקריאה נוספת
[עריכת קוד מקור | עריכה]- Dirac, Paul A.M. (1982). Principles of quantum mechanics. Oxford University Press. ISBN 0-19-852011-5.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Halzen, Francis & Martin, Alan D. (1984). QUARKS AND LEPTONS: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2
- The Particle Data Group
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- מספר קוונטי, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים
[עריכת קוד מקור | עריכה]- ^ Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN 0-19-855148-7
- ^ Concepts of Modern Physics (4th Edition), A. Beiser, Physics, McGraw-Hill (International), 1987, ISBN 0-07-100144-1
- ^ Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd Edition), R. Eisberg, R. Resnick, John Wiley & Sons, 1985, ISBN 978-0-471-87373-0
- ^ Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry (Volume 1), P.W. Atkins, Oxford University Press, 1977, ISBN 0-19-855129-0
- ^ Quantum Mechanics (2nd edition), Y. Peleg, R. Pnini, E. Zaarur, E. Hecht, Schuam's Outlines, McGraw Hill (USA), 2010, ISBN 978-0-07-162358-2
- ^ Molecular Quantum Mechanics Parts I and II: An Introduction to QUANTUM CHEMISTRY (Volume 1), P. W. Atkins, Oxford University Press, 1977, ISBN 0-19-855129-0
- ^ Molecular Quantum Mechanics Part III: An Introduction to QUANTUM CHEMISTRY (Volume 2), P. W. Atkins, Oxford University Press, 1977





![{\displaystyle I_{\mathrm {3} }={\frac {1}{2}}\left[\left(n_{\mathrm {u} }-n_{\mathrm {\bar {u}} })-(n_{\mathrm {d} }-n_{\mathrm {\bar {d}} }\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7d30a972f39268c712a210450a733022041797a)















































































