יחס מיקוד
יחס מיקוד (או מספר f.[1], באנגלית: f-number, f/#, F-number, F Stop Number, F-stop או F#) הוא פרמטר חסר ממדים המתאר את יכולת איסוף האור של מערכת אופטית, כגון עדשת מצלמה. הוא מוגדר בתור היחס בין אורך המוקד של מערכת לקוטר אישון הכניסה שלה[2][3][4], ומהווה גורם עיקרי בקביעת עומק השדה, בעקיפה ובחשיפה של תמונה.[5]
ניתן להסתכל על יחס מיקוד כעל הערך ההופכי של המפתח היחסי (קוטר אישון הכניסה חלקי אורך המוקד)[6] המציין כמה אור יכול לעבור דרך מערכת בעלת אורך מוקד מסוים. יחס מיקוד קטן יותר משמעותו מפתח יחסי גדול יותר, כלומר כמות גדולה יותר של אור נכנסת למערכת, ולהפך.
יחס המיקוד קשור למפתח הנומרי של המערכת, המתאר את זווית איסוף האור לתוך רכיב אופטי. המפתח הנומרי לוקח בחשבון גם את מקדם השבירה של המרחב בו המערכת פעילה, בעוד שיחס המיקוד אינו לוקח גודל זה בחשבון.
הגדרה
[עריכת קוד מקור | עריכה]יחס המיקוד מוגדר באופן הבא: כאשר אורך המוקד, קוטר אישון הכניסה (המפתח האפקטיבי) ו־ הוא יחס המיקוד, או מספר ה־f.
נהוג לציין מספרי f כשלפניהם הסימן "f/", מה שגורם לסימון להיראות כמו ביטוי מתמטי עבור קוטר אישון הכניסה כתלות באורך המוקד [2]. למשל, עבור עדשה בעלת אורך מוקד של 10 מ"מ וקוטר של 5 מ"מ, יחס המיקוד יהיה שווה ל־2 ויסומן כ־"f/2", כאשר בסימון זה נרמז כי הקוטר שווה למחצית אורך המוקד.
לרוב העדשות יש צמצם מתכוונן המאפשר למשתמש לשנות את יחס המיקוד בהתאם לצרכיו. בהזנחת יעילות העברת האור, עדשה בעלת יחס מיקוד גדול יותר תעביר פחות אור ותקרין תמונות כהות יותר. עוצמת ההארה של התמונה עומדת ביחס הפוך לריבוע של יחס המיקוד ביחס לבהיקות (אנ') הדמות בשדה הראייה של העדשה.
לדוגמה, לעדשת f/4 עם אורך מוקד של 100 מ"מ יהיה קוטר של 25 מ"מ, בעוד שלעדשת f/2 בעלת אורך מוקד זהה יהיה קוטר של 50 מ"מ. מכיוון שהשטח מתכונתי לריבוע של קוטר העדשה[7], כמות האור הנכנסת לעדשת f/2 גדולה פי ארבעה מכמות האור הנכנסת לעדשת f/4. על מנת לקבל חשיפת צילום זהה עבור שתי העדשות, יש להפחית פי ארבעה את זמן החשיפה של עדשת ה־f/2.
לעומת זאת, לעדשת f/4 עם אורך מוקד של 200 מ"מ יהיה קוטר של 50 מ"מ. עדשה זו בעלת שטח גדול פי ארבעה מעדשת ה־f/4 בעלת אורך מוקד של 100 מ"מ (כי קוטרה 25 מ"מ), ולכן כמות האור שנאספת על ידי עדשה זו גדולה גם היא פי ארבעה. אולם נשים לב שעדשת ה־200 מ"מ גם מקרינה תמונה גבוהה פי שניים ורחבה פי שניים מהתמונה שמקרינה עדשת ה־100 מ"מ, ולכן עוצמות ההארה במישור המוקד של שתי העדשות תהיינה זהות עבור אותה התמונה – בהתאמה לכך שלשתיהן אותו יחס מיקוד.
יחס המיקוד מתאר את כמות האור שמגיע אל מפתח העדשה, אך כדי לדעת כמה אור מגיע בפועל אל מישור המוקד יש להתחשב בהעברה של המערכת (כלומר, איזה חלק מהאור לא מוחזר או נבלע על ידי הרכיבים האופטיים). לשם כך מקובל להגדיר את ה־T-stop, מקבילה של יחס המיקוד הלוקחת בחשבון את נצילות העברת האור.
מגבלות על יחס המיקוד
[עריכת קוד מקור | עריכה]
על מנת לטשטש את הרקע בתמונה כדי להבליט את האובייקט, מה שנקרא בוקה, נהוג להשתמש בעדשות עם יחס מוקד של 2.8 או אפילו 1.4. לעיתים קרובות מוצאים עדשות זום שלהן מיפתח אפקטיבי קטן יותר בצילומי תקריב (zoom-in) מאשר ב־zoom-out. זו הסיבה שלעיתים מוצאים עדשות עם יחס מיקוד שונה לכל אורך מוקד, לדוגמה: 18-55mm f/3.5-5.6 (עדשה לה מיפתח של כ־5 מ"מ באורך מוקד של 18 מ"מ (תקריב) לעומת מפתח של 9.8 מ"מ באורך מוקד של 55 מ"מ).[8]
יחס המיקוד הנמוך ביותר הזמין (נכון ל־2022) הוא f/0.7, בעדשה שנקראת Zeiss Planar 50mm (אנ'), עדשה ששימשה את נאס"א לצילום הירח ואת סטנלי קיובריק לצילום סרט לאור נרות. רוב העדשות המסחריות מגיעות ל־f/2, מיעוטן מגיעות ל־f/1.4 ומעטות מאוד מגיעות ל־f/0.95.[8]
יחס המיקוד הגבוה ביותר הוא f/45 והוא שייך לעדשת מאקרו בעלת עומק מוקד גדול במיוחד: Sigma 105mm f/2.8 EX DG Macro. יחס מוקד של f/40 זמין בעדשה בשם Itorex 50mm. מרבית העדשות המסחריות מגיעות ללא יותר מ־f/32 או f/16.[8]
קונבנציית f-stop וחשיפה
[עריכת קוד מקור | עריכה]
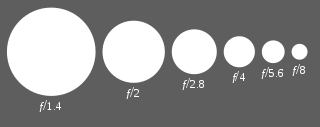
בצילום, המונח סטופ (stop, בעברית "מעצור") הוא יחידת מידה לכימות יחסים של חשיפה או אור, כאשר כל סטופ שמתווסף תורם פקטור של שתיים וכל סטופ שמופחת תורם פקטור של חצי. סטופ של 1 ידוע גם בתור יחידת EV (Exposure Value – ערך החשיפה). באופן מסורתי, הגדרת הצמצם במצלמה נעשית בצעדים בדידים המכונים f-stops. כל סטופ מסומן ביחס המיקוד התואם לו ומייצג מחצית מעוצמת האור של הסטופ הקודם, כלומר חצייה של שטח אישון הכניסה. מכיוון שאישון הכניסה מעגלי, חצייה של שטחו שקולה להקטנת קוטרו פי (כ־0.7071). ברוב העדשות המודרניות קיימת סקלת f-stops סטנדרטית המבוססת על סדרה הנדסית של חזקות של שורש 2: f/1, f/1.4, f/2, f/2.8, f/4, f/5.6 וכן הלאה, כאשר כל איבר בסדרה נמוך בסטופ אחד מהקודם לו משמאל וגבוה בסטופ אחד מהעוקב לו מימין. הסדרה לעיל מתקבלת מעיגול איברי הסדרה ההנדסית למספרים רציונליים (על מנת להקל על כתיבתם): באותו אופן שבו f-stop אחד תואם לפקטור של שניים בעוצמת האור, מהירויות התריס מסודרות כך שכל מהירות שונה פי שניים משכנתה. הרחבת העדשה בסטופ בודד מאפשרת לכמות כפולה של אור לפגוע בסרט הצילום בפרק זמן נתון. כדי לקבל חשיפה זהה בצמצם הגדול יותר, התריס ייפתח למחצית מזמן זה, כלומר מהירותו גדלה פי 2. לרוב הסרט יגיב באופן דומה בשני המקרים עקב תכונת ההדדיות (זה לא מתקיים בזמני חשיפה ארוכים או קצרים במיוחד בהם יש כשל בתכונה זו). קיים קשר בין הצמצם, מהירות התריס ורגישות סרט הצילום: עבור בהיקות קבועה, הכפלת שטח הצמצם, הקטנת מהירות התריס פי שניים או שימוש בסרט בעל רגישות כפולה כולם בעלי אפקט זהה על התמונה החשופה. למטרות מעשיות דיוק מוחלט אינו נדרש (מהירויות תריס מכניות ידועות כלא מדויקות עקב בלאי, אך ההשפעה על החשיפה זניחה). אין זה משמעותי שמהירויות התריס ושטחי הצמצם לא משתנים בפקטור של שניים בדיוק. לעיתים צלמים מתייחסים ליחסי חשיפה אחרים כאל סטופים. תוך התעלמות מסימני מספרי ה־f, ה־f-stops יוצרים סולם לוגריתמי של עוצמת החשיפה. במוחים הללו, ניתן לבצע מחצית של צעד בסולם כדי לקבל הבדל של חצי סטופ בחשיפה.
סטופים חלקיים
[עריכת קוד מקור | עריכה]לרוב המצלמות במאה העשרים היה מפתח בעל גודל משתנה באופן רציף עם סימונים של סטופים שלמים. בשנות ה־60 נכנס לשימוש צמצם עצור לחיצה שהשמיע קליק בכל מחצית סטופ ובכל סטופ שלם. במצלמות מודרניות, יחס המיקוד לרוב מחולק לחלקים רבים יותר מסטופ בודד. צעדים של שליש סטופ (1/3 EV) הם הנפוצים ביותר, מכיוון שהם תואמים את מערכת ה־ISO של מהירות סרט. במצלמות מסוימות נעשה שימוש בצעדים של חצי סטופ. לרוב הסטופים השלמים מסומנים ועצירות הביניים משמיעות קליק. לדוגמה, המפתח הקטן בשליש סטופ מ־f/2.8 הוא f/3.2, המפתח הקטן בשליש נוסף הוא f/3.5 והמפתח הקטן בסטופ שלם הוא f/4. ה־f-stops הבאים בסדרה זו הם: חישוב הצעדים בסטופ שלם (1 EV) נעשה באופן הבא: חישוב הצעדים בחצי סטופ (EV 1/2): חישוב הצעדים בשליש סטופ (1/3 EV): כמו בסטנדרטי מהירויות הסרט בעבר (DIN ו־ASA), מהירות ה־ISO מוגדרת במרווחים של שליש סטופ בלבד, ומהירויות הצמצם של מצלמות דיגיטליות לרוב בעלת סקאלה דומה של שניות הופכיות. הסדרה הבאה היא חלק מטווח ה־ISO: כאשר השניות ההופכיות בעלות מספר הבדלים בערכיהן (1/15, 1/30 ו־1/60 שניות במקום 1/16, 1/32 ו־1/64) מטעמי קונבנציה. בפועל, גודל המפתח המקסימלי של עדשה אינו בחזקת מספר שלם אלא בחזקת חצי או שני שלישים. עדשות מתחלפות חשמליות הקיימות במצלמות SLR הן בעלות מרווחים פנימיים של 1/8 סטופ, כך שהגדרת ה־1/3 סטופ של המצלמה ממוקמת סביב ה־1/8 הקרוב ביותר של העדשה.
סקאלה סטנדרטית של מספרי f עם סטופים שלמים
[עריכת קוד מקור | עריכה]נסמן: כאשר הוא גודל המפתח. מספרי f קונבנציונליים מחושבים בסדרת סטופים שלמים:
| AV | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.5 | 0.7 | 1.0 | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 | 45 | 64 | 90 | 128 | 180 | 256 |
| calculated | 0.5 | 0.707... | 1.0 | 1.414... | 2.0 | 2.828... | 4.0 | 5.657... | 8.0 | 11.31... | 16.0 | 22.62... | 32.0 | 45.25... | 64.0 | 90.51... | 128.0 | 181.02... | 256.0 |
סקאלה טיפוסית של מספרי f עם חצאי סטופים
[עריכת קוד מקור | עריכה]| AV | 1- | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 1.0 | 1.2 | 1.4 | 1.7 | 2 | 2.4 | 2.8 | 3.3 | 4 | 4.8 | 5.6 | 6.7 | 8 | 9.5 | 11 | 13 | 16 | 19 | 22 | 27 | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 107 | 128 |
סקאלה טיפוסית של מספרי f עם שלישי סטופים
[עריכת קוד מקור | עריכה]| AV | 1- | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 | 36 | 40 | 45 | 51 | 57 | 64 | 72 | 80 | 90 |
לעיתים אותו המספר קיים במספר סקאלות שונות, למשל נעשה שימוש במפתח של f/1.2 גם במערכת של חצי סטופ[9] וגם במערכת של שליש סטופ[10]. [8] לעיתים נעשה שימוש ב־f/1.3, f/3.2 ובערכים נוספים בסקאלת השליש סטופ.[11]
סקאלה טיפוסית של מספרי f עם רבעי סטופים
[עריכת קוד מקור | עריכה]| AV | 0 | 1 | 2 | 3 | 4 | 5 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.7 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3.1 | 3.3 | 3.7 | 4 | 4.4 | 4.8 | 5.2 | 5.6 |
| AV | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 5.6 | 6.2 | 6.7 | 7.3 | 8 | 8.7 | 9.5 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 |
H-Stop
[עריכת קוד מקור | עריכה]H-סטופ (H מהמילה hole, חור באנגלית) הוא השקול ליחס המיקוד עבור חשיפה אפקטיבית, המבוסס על השטח המכוסה בחורים בדיסקי דיפוזיה או במפתחי מסננת הנמצאים בעדשות Rodenstock Imagon (אנ).
T-Stop
[עריכת קוד מקור | עריכה]T-סטופ (T מהמילה transmission, העברה באנגלית), הוא יחס המיקוד המותאם לנצילות העברת האור. עדשה בעלת T-סטופ בגודל N מקרינה תמונה בעלת בהירות זהה לעדשה אידיאלית בעלת העברה של 100% ויחס מיקוד בגודל N. T-סטופ מחושב על ידי חילוק יחס המיקוד בשורש נצילות העברת האור של העדשה: לדוגמה, f/2.0 של עדשה עם נצילות העברת אור של 75% תהיה בעלת T-stop של 2.3: מכיוון שלעדשות לא אידיאליות יש נצילות העברת אור של פחות מ־100%, ה־T סטופ של עדשה תמיד גדול יותר מיחס המיקוד שלה.[12] עם הפסדים של 8% במשטחי זכוכית-אוויר בעדשות ללא ציפוי, ציפוי רב שכבתי הוא המפתח להפחתת הפסדי העברת האור בתכנון עדשות.[13][14] לעיתים נעשה שימוש ב־T סטופים במקום במספרי f כדי לייצג חשיפה, במיוחד כאשר נעשה שימוש במדדי אור חיצוניים.[15]נצילות העברת אור בעדשות טיפוסיות נעה לרוב בין 60% ל־90%.[16] בעולם הקולנוע לרוב נעשה שימוש ב־T סטופים, כאשר תמונות רבות מוצגות בזו אחר זו וכל הבדל מזערי בחשיפה עשוי להיות משמעותי. עדשות של מצלמות קולנוע לרוב מותאמות ל־T סטופים ולא למספרי f.[15] בצילום סטילס אין צורך בעקביות מוחלטת בין עדשות המצלמה ולכן הבדלי חשיפה קטנים נוטים להיות פחות משמעותיים. יחד עם זאת, בעדשות מיוחדות כמו Smooth Trans Focus של חברות מינולטה וסוני עדיין נעשה שימוש ב־T סטופים.
יחס מיקוד תלוי תדר
[עריכת קוד מקור | עריכה]בצילום, יחס המיקוד הוא בעל ערכים קבועים. לעומת זאת, במצבים מסוימים ישנה עדיפות לשימוש במספרי f תלויי תדר; בעולם האולטרסאונד מספרי f קבועים ממזערים את האונות המשניות בהדמיה שנעשית באמצעות פולסים מהירים של גלי קול, אך מייצרים תת-מפתחים דינאמיים שגודלם משתנה יחד עם נקודות המוקד. תת-המפתחים הללו מתעלמים מרכיבי התדר הנמוך של גלי ה־RF, מה שמקטין את הרזולוציה הרוחבית. מספרי f התלויים בתדר מצמצמים את תופעה זו: בתדרים גבוהים הם מקטינים את תת-המפתחים הנוצרים, מה שמוביל להסרה של רכיבי RF בעלי דגימה מרחבית נמוכה ומזעור האונות המשניות. בתדרים נמוכים, מספרי ה־f מגדילים את תת-המפתחים מה שמאפשר שימוש בכל הרכיבים של גלי ה־RF ושימור הרזולוציה המרחבית.[17] יחס המיקוד תלוי התדר מחושב באופן הבא: כאשר יחס המיקוד, הוא אורך המוקד בתדר f ו־A הוא קוטר תת-המפתח התלוי ב־.
כלל סאני 16
[עריכת קוד מקור | עריכה]כלל סאני 16 (sunny 16 rule) הוא דוגמה לשימוש במספרי f בעולם הצילום: חשיפה מדויקת כמעט לחלוטין תתקבל כאשר משתמשים בצמצם בעל f/16 ומהירות תריס קרובה לאחד חלקי מהירות ה־ISO של הסרט ביום שמשי. למשל, אם נשתמש ב־ISO בגודל 200, בצמצם בעל f/16 ומהירות תריס של 1/200 תתקבל חשיפה מדויקת בקירוב. עבור תאורה נמוכה יותר ניתן להקטין את יחס המיקוד ש"יפתח" את העדשה (הגדלה של יחס המיקוד "תסגור" את העדשה, בהתאמה).
השפעה על חדות התמונה
[עריכת קוד מקור | עריכה]

עומק השדה גדל יחד עם יחס המיקוד. תמונות שצולמו עם יחס מיקוד נמוך (מפתח גדול יותר) נוטות להתמקד באובייקט במרחק מסוים, כאשר יתר התמונה מטושטשת. לרוב נעשה שימוש באפקט זה בצילומי טבע ובצילומי דיוקן מכיוון שטשטוש הרקע מבליט את האובייקט הרצוי, מה שמייצר תמונה אסתטית יותר. בהינתן יחס מיקוד מסוים, עומק השדה של תמונה תלוי במספר פרמטרים נוספים, לרבות אורך המוקד, מרחק הדמות ופורמט הסרט או הגלאי בו התמונה נקלטת. עומק השדה ניתן לתיאור גם בעזרת זווית הראייה, מרחק הדמות וקוטר אישון הכניסה. כתוצאה מכך, עבור ערכים זהים של יחסי מיקוד, זוויות ראייה ואורכי מוקד, פורמט סרט קטן יותר יהיה בעל יהיה בעל שדה עמוק יותר מאשר פורמט סרט גדול יותר. זאת משום שעבור נתונים אלה פורמט סרט קטן יותר זקוק לאורך מוקד קצר יותר (זווית עדשה רחבה יותר) כדי לקבל את אותה זווית ראייה, ועומק השדה גדל כאשר אורך המוקד קטן. מכאן שעל מנת להקטין תופעות עומק שדה יש להשתמש ביחסי מיקוד קטנים יותר (וייתכן שבאופטיקה מורכבת יותר) במצלמות בעלות פורמט סרט קטן מאשר במצלמות עם פורמט סרט גדול יותר. בנוסף לפוקוס, חדות התמונה קשורה ליחסי מיקוד בשני סוגים של אפקטים אופטיים: אברציות, שנגרמות כתוצאה מתכנון לקוי של עדשה, ודיפרקציה, שנובעת מההתנהגות הגלית של אור.[18] מכאן שיחס המיקוד האופטימלי תלוי בתכנון העדשה. עבור עדשות מודרניות סטנדרטיות המורכבות מ־6 או 7 חלקים, התמונה החדה ביותר לרוב מתקבלת סביב f/5.6-f/8, לעומת זאת, בעדשות ישנות יותר בעלות 4 חלקים בלבד (משוואת Tessar), התמונה החדה ביותר תתקבל עבור f/11. ככל שעדשה מודרנית מורכבת מיותר אלמנטים, כך ניתן להקטין את האברציות ולקבל תמונה חדה יותר עבור מספרי f קטנים. עבור מפתחים קטנים, ניתן לשפר את עומק השדה ואת האברציות אך הדיפרקציה תיצור פיזור גדול יותר של אור שמייצר טשטוש. בהירות התמונה מושפעת גם היא מיחס המיקוד, עבור עדשות בעלות זוויות ראייה רחבות ומפתח גדול יתקבלו קצוות תמונה חשוכים יותר (ויגנט). בפועל, אין צורך לדייק מאוד בפרטים הטכניים בצילום באור יום. ברוב מצבי התאורה, f/8 (עבור פורמט סרט של 35 מ"מ או יותר) מייצר עומק שדה ומהירות עדשה טובים עבור חשיפה בסיסית מספקת.[19]
העין האנושית
[עריכת קוד מקור | עריכה]על מנת לחשב את יחס המיקוד של העין האנושית יש למצוא את המפתח הפיזיקלי ואת אורך המוקד שלה. קוטר האישון יכול להגיע ל־6–7 מ"מ כאשר הוא פתוח לרווחה, וזהו המפתח המקסימלי. יחס המיקוד של העין האנושית נע בין f/8.3 במקום מואר ל־f/2.1 בחושך.[20] על מנת לחשב את אורך המוקד יש לקחת בחשבון את תכונות שבירת האור של נוזלי העין, לכן לא ניתן להתייחס לעין כאל מצלמה מלאה באוויר עם עדשה אידיאלית.
היחס הפוקאלי בטלסקופ
[עריכת קוד מקור | עריכה]
באסטרונומיה, יחס המיקוד מכונה לרוב בתור יחס פוקאלי (f-ratio) ומסומן ב־N. הוא עדיין מוגדר בתור היחס בין אורך המוקד f לקוטר העדשה D: למרות שתכונות היחס הפוקלי נשמרות, המצבים בהם משתמשים בו עשויים להשתנות. בצילום, היחס הפוקלי משנה את ההארה של המרחב הפוקלי (או את ההספק האופטי ליחידת שטח של התמונה) ומשמש לשליטה במשתנים כגון עומק השדה. כאשר משתמשים בטלסקופ אופטי באסטרונומיה, אין משמעות לעומק השדה והבהירות של גורמי שמיים נקודתיים במונחים של הספק אופטי כולל (לא מחולק ליחידת שטח) היא פונקציה של שטח המפתח בלבד, ללא תלות באורך המוקד. אורך המוקד משפיע על שדה הראייה של המכשיר ועל הסקאלה של התמונה שמוקרנת במרחב הפוקוס. לדוגמה, טלסקופ מסוג SOAR באורך 4 מטרים בעל שדה ראייה קטן (כ־f/16) ושימושי למחקרי כוכבים. טלסקופ מסוג LSST באורך 8.4 מטרים המסוגל לכסות את השמיים בשלמותם בכל שלושה ימים הוא בעל שדה ראייה רחב ביותר ואורך מוקד קצר מאוד של 10.3 מטרים (f/1.2), המתאפשר של ידי מערכת תיקון שגיאות.[21]
משוואת המצלמה (#G)
[עריכת קוד מקור | עריכה]משוואת המצלמה (או #G) היא היחס בין הקרינה המגיעה לחיישן המצלמה לבין הקרינה במישור המוקד של עדשת המצלמה:[22] כאשר τ הוא מקדם ההעברה של העדשה והיחידות הן בסטרדיאן (sr−1).
יחס מיקוד אפקטיבי
[עריכת קוד מקור | עריכה]יחס המיקוד מייצג את יכולת איסוף האור של עדשה באופן מדויק רק כאשר האובייקט נמצא במרחק אינסופי.[23] בצילום לרוב מתעלמים ממגבלה זו ונעשה שימוש ביחס המיקוד למרות מרחק האובייקט. בתכנון אופטי, לרוב יש צורך באלטרנטיבה עבור מערכות בהן האובייקט קרוב לעדשה. במקרים הללו נעשה שימוש ב־Nw, יחס מיקוד אפקטיבי:[23] כאשר N הוא יחס המיקוד, NAi הוא המפתח הנומרי במישור התמונה של העדשה, הוא הערך המוחלט של ההגדלה של העדשה עבור אובייקט הנמצא במרחק מסוים ו־P הוא ההגדלה של האישון. מאחר שהגדלת האישון לרוב אינה ידועה, בדרך כלל מניחים שערך זה שווה ל־1 (הערך של P בכל עדשה סימטרית). בצילום המשמעות היא שככל שמתמקדים קרוב יותר, המפתח האפקטיבי של המצלמה קטן מה שמכהה את החשיפה. יחס המיקוד האפקטיבי לרוב מתואר בצילום כיחס המיקוד המתוקן של הארכת העדשה על ידי פקטור בלוז (Bellows factor), אשר בעל חשיבות בצילום מאקרו.
היסטוריה
[עריכת קוד מקור | עריכה]מערכת מספרי ה־f לתיאור מפתחים יחסיים התפתחה בשלהי המאה ה־19, יחד עם מספר מערכות נוספות.
מקורות של מפתחים יחסיים
[עריכת קוד מקור | עריכה]בשנת 1867, "יחס המפתח" הוגדר על ידי סאטון ודוסון באופן הדדי ליחס המיקוד המודרני. בציטוט הבא, "יחס מפתח" של 1/24 מחושב בתור היחס בין 150 מ"מ (6 אינץ') ל־6.4 מ"מ (0.25 אינץ'), התואם ל־f/24:
בכל עדשה קיים, בהתאמה ליחס מפתח נתון (כלומר, היחס בין קוטר המעצור לאורך המוקד), מרחק מסוים של עצם קרוב ממנו, שבינו לבין האינסוף כל העצמים בפוקוס זהה. למשל, בעדשה בעלת אורך מוקד של 6 אינץ' וסטופ של 1/4 אינץ' (יחס מפתח של אחד חלקי עשרים וארבע), כל העצמים הממוקמים במרחקים בין 20 רגל מהעדשה למרחק אינסופי ממנה (כוכב במיקום קבוע, למשל) נמצאים בפוקוס טוב באותה המידה. עשרים רגל נקרא אפוא 'טווח המוקד' של העדשה עבור הסטופ הנ"ל. לכן, טווח הפוקוס הוא המרחק בין האובייקט הקרוב ביותר הנמצא במיקוד טוב כאשר זכוכית הקרקע מותאמת לעצם רחוק מאוד. עבור אותה העדשה, טווח הפוקוס יהיה תלוי בגודל הדיאפרגמה בה נעשה שימוש, כאשר בעדשות שונות בעלות יחס מפתח זהה, טווחי הפוקוס יתרחקו ככל שאורך מוקד העדשה יוגדל. הביטויים 'יחס המפתח' ו'טווח פוקוס' טרם נכנסו לשימוש רווח, אך רצוי מאוד שזה יקרה, על מנת למנוע עמימות בהתייחסות לתכונות של עדשות צילום.[24]
בשנת 1874, ג'ון הנרי דלמייר קרא ליחס "יחס העוצמה" של עדשה:
המהירות של עדשה תלויה ביחס בין המפתח למוקד השקול. על מנת לוודא זאת, יש לחלק את המוקד השקול בקוטר של המפתח האפקטיבי של העדשה המדוברת; ולכתוב את המנה בתור המכנה עם 1, או יחידה, עבור המונה. לכן למציאת היחס בין עדשה בעלת קוטר של 2 אינצ'ים ומוקד של 6 אינצ'ים, יש לחלק את המוקד במפתח, או 6 חלקי 2 שווה 3; מכאן, 1/3 הוא יחס העוצמה. [25]
למרות שטרם נחשף לתאוריית המעצורים והאישונים של ארנסט אבה[26] שפורסמה לקהל הרחב על ידי זיגפריד צ'פסקי ב־1893[27], דלמייר הבחין בין המפתח האפקטיבי שהגדיר וקוטר המפתח:
יש לשים לב, שכדי למצוא את יחס העוצמה האמיתי, יש לוודא את הקוטר של המפתח האפקטיבי. ניתן לבצע זאת בקלות במקרה של עדשה יחידה או עדשות כפולות שלובות בעלות פתח מלא, אלו דורשות יישום של זוג מצפנים; אולם בשימוש בעדשות בשילוב כפול או משולש, בהכנסת מעצורים בין השילובים, זה מעט יותר בעייתי; ברור שבמקרה זה הקוטר של המעצור המוכנס אינו מייצג את קרן האור המועברת על ידי הצירוף הקדמי. על מנת לוודא זאת, יש למקד אובייקט רחוק, להסיר את המסך הממקד ולהחליפו בשקף קולודיון, כאשר הפלטה המוכנה הוחלפה לפני כן בחתיכת קרטון. יש לחורר חור קטן ועגול במרכז הקרטון ולהעביר את המערכת לחדר חשוך. יש להדליק נר על יד החור ולצפות באזור המואר הנראה בקדמת המערכת; קוטרו של מעגל זה, הנמדד בקפידה, הוא המפתח האפקטיבי האמיתי של העדשה עבור המעצור הנ"ל.[25]
נקודה זו הודגשה על ידי צ'פסקי בשנת 1983.[27] לפי סקירה באנגלית שנעשתה לספרו ב־1894, "יש לבצע הפרדה ברורה בין מפתח אפקטיבי וקוטרו של מעצור פיזי".[28] בנו של ג. ה. דלמייר, תומאס רודולפוס דלמייר, ממציא עדשת הטלפוטו, המשיך את השימוש בביטוי יחס העוצמה ב־1899.[29]
מערכות מספור מפתחים
[עריכת קוד מקור | עריכה]
במקביל, פותחו מספר מערכות למספור מפתחים במטרה לקבוע זמני חשיפה ביחס פרופורציונלי (ישיר או הופכי) למפתח, במקום לריבוע יחס המיקוד או לריבוע ההופכי של יחס המפתח או יחס העוצמה. אולם, המערכות הללו כללו קבוע כלשהו, בניגוד ליחס הפשוט בין אורך המוקד לקוטר המפתח. לדוגמה, המערכת האחידה (Uniform System – U.S) של מפתחים נקבעה בתור סטנדרט על ידי אחוות הצילום של בריטניה בשנות ה־1880. לדברי בות'למיי "הסטופים של כל היצרנים כעת מסודרים לפי מערכת זו" (1891).[30] U.S. של 16 הוא מפתח זהה ל־f/16, אולם במפתחים גדולים או קטנים בסטופ מלא נעשית הכפלה פי 2 או פי חצי של מספר ה־U.S., למשל ערכו של f/11 ב־U.S. הוא 8, וערכו של f/8 ב־U.S. הוא 4. זמן החשיפה הנדרש פרופורציונלי באופן ישיר למספר ה־U.S.. איסטמן קודאק השתמשו במערכת ה־U.S. במצלמות רבות עד לשנות ה־20 של המאה הקודמת. עד 1895, הודג'ס סתר את בות'למיי ולדבריו מערכת מספרי ה־f החליפה את מערכת ה־U.S.: "זו נקראת מערכת ה־f/x, והדיאפרגמות של כל העדשות המודרניות המיוצרות היטב מסומנות כך".[31] להלן טבלת השוואות בין מספרי דיאפרגמות מ־1899:
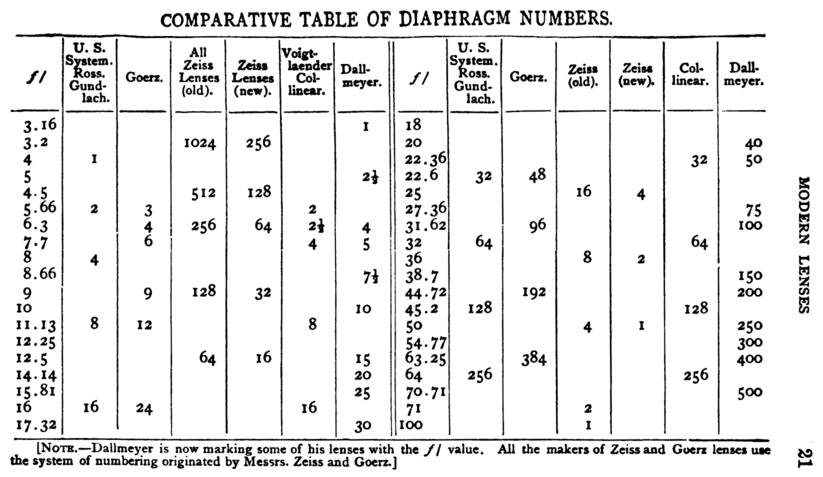
ב־1901[32] פייפר דן בחמש מערכות שונות של סימון מפתחים: מערכות צייס ישנות וחדשות המבוססות על העוצמה בפועל (פרופורציונלית לריבוע ההופכי של יחס המיקוד); ומערכות ה־U.S., C.I. ודלמייר המבוססות על חשיפה (פרופורציונליות לריבוע יחס המיקוד). הוא קרא למספר ה־f "מספר היחס", "מספר יחס המפתח" ו"יחס המפתח". הוא קרא לביטויים כמו f/8 "הקוטר החלקי" של המפתח, למרות שהוא שקול לחלוטין ל"קוטר המוחלט" שהוא מבדיל עם ביטוי שונה. הוא לעיתים השתמש בביטוים כמו "מפתח של f 8 ", ללא סימן החלוקה. ב־1902 בק ואנדרוס דנו בסטנדרט של f/4, f/5.6, f/8, f/11.3 וכו'[33] של אחוות הצילום המלכותית (Royal Photographic Society – R.P.S). R.P.S שינו את שמם ועברו להשתמש במערכת ה־U.S. בין השנים 1895 ו־1902.
סטנדרטיזציה טיפוגרפית
[עריכת קוד מקור | עריכה]

עד 1920 הביטוי f-number הופיע בספרות הן כ־F number והן כ־f/number. בפרסומים מודרניים, התצורות f-number ו־f number נפוצות יותר, אך לעיתים ניתן לפגוש בביטויים ישנים יותר.[34] בתחילת המאה ה־20 הסימונים ליחסי מיקוד נטו להיות מגוונים וכללו בין היתר אות גדולה F,[35] נקודה במקום הקו הנטוי[36] ולעיתים הופיעו בתצורת שבר אנכי.[37] סטנדרט ה־ASA משנת 1961, PH2. 12-1961 (סטנדרט אמריקאי כלל שימושי למטרי חשיפה צילומית), מצין ש"הסימון למפתחים יחסיים יהיה f/ או f: שלאחריו יופיע יחס המיקוד האפקטיבי".
ראו גם
[עריכת קוד מקור | עריכה]הערות שוליים
[עריכת קוד מקור | עריכה]- ^ f number, באתר האקדמיה ללשון העברית
- ^ 1 2 Smith, Warren ‘‘Modern Optical Engineering’’, 4th Ed., 2007 McGraw-Hill Professional, p. 183.
- ^ Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. p. 152. ISBN 0-201-11609-X.
- ^ Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. Bellingham, Wash: SPIE. p. 29. ISBN 9780819452948. OCLC 53896720.
- ^ Smith, Warren ‘‘Modern Lens Design’’ 2005 McGraw-Hill.
- ^ ISO, Photography—Apertures and related properties pertaining to photographic lenses—Designations and measurements, ISO 517:2008
- ^ ראה שטח מעגל.
- ^ 1 2 3 Suzee Skwiot, What Is F-Stop & How to Use It for Photography - Adorama, Adorama.com, 2021-03-11 (באנגלית אמריקאית)
- ^ Harry C. Box (2003). Set lighting technician's handbook: film lighting equipment, practice, and electrical distribution (3rd ed.). Focal Press. ISBN 978-0-240-80495-8.
- ^ Paul Kay (2003). Underwater photography. Guild of Master Craftsman. ISBN 978-1-86108-322-7.
- ^ David W. Samuelson (1998). Manual for cinematographers (2nd ed.). Focal Press. ISBN 978-0-240-51480-2.
- ^ Transmission, light transmission (אורכב 08.05.2021 בארכיון Wayback Machine), DxOMark
- ^ Sigma 85mm F1.4 Art lens review: New benchmark (אורכב 04.01.2018 בארכיון Wayback Machine), DxOMark
- ^ Colour rendering in binoculars and lenses - Colours and transmission (אורכב 04.01.2018 בארכיון Wayback Machine), LensTip.com
- ^ 1 2 "Kodak Motion Picture Camera Films". Eastman Kodak. בנובמבר 2000. אורכב מ-המקור ב-2002-10-02. נבדק ב-2 בספטמבר 2007.
{{cite web}}: (עזרה) - ^ "Marianne Oelund, "Lens T-stops", dpreview.com, 2009". ארכיון מ-2012-11-10. נבדק ב-2013-01-11.
- ^ Schniffer, Martin F. and Smith, George. 2021 IEEE Int. Ultrasonics Symp. (IUS), Xi’an, China, Sep. 2021, pp. 1–4. DOI: 10.1109/IUS52206.2021.9593488 [1]
- ^ Michael John Langford (2000). Basic Photography. Focal Press. ISBN 0-240-51592-7.
- ^ Levy, Michael (2001). Selecting and Using Classic Cameras: A User's Guide to Evaluating Features, Condition & Usability of Classic Cameras. Amherst Media, Inc. p. 163. ISBN 978-1-58428-054-5.
- ^ Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 0-201-11609-X. Sect. 5.7.1
- ^ Charles F. Claver; et al. (19 במרץ 2007). "LSST Reference Design" (PDF). LSST Corporation: 45–50. אורכב מ-המקור (PDF) ב-6 במרץ 2009. נבדק ב-10 בינואר 2011.
{{cite journal}}: (עזרה); Cite journal requires|journal=(עזרה) - ^ Driggers, Ronald G. (2003). Encyclopedia of Optical Engineering: Pho-Z, pages 2049-3050 (באנגלית). CRC Press. ISBN 978-0-8247-4252-2. נבדק ב-18 ביוני 2020.
{{cite book}}: (עזרה) - ^ 1 2 Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 0-8194-5294-7. p. 29.
- ^ Thomas Sutton and George Dawson, A Dictionary of Photography, London: Sampson Low, Son & Marston, 1867, (p. 122).
- ^ 1 2 John Henry Dallmeyer, Photographic Lenses: On Their Choice and Use – Special Edition Edited for American Photographers, pamphlet, 1874.
- ^ Southall, James Powell Cocke (1910). "The principles and methods of geometrical optics: Especially as applied to the theory of optical instruments". Macmillan: 537.
theory-of-stops.
{{cite journal}}: Cite journal requires|journal=(עזרה) - ^ 1 2 Siegfried Czapski, Theorie der optischen Instrumente, nach Abbe, Breslau: Trewendt, 1893.
- ^ Henry Crew, "Theory of Optical Instruments by Dr. Czapski," in Astronomy and Astro-physics XIII pp. 241–243, 1894.
- ^ Thomas R. Dallmeyer, Telephotography: An elementary treatise on the construction and application of the telephotographic lens, London: Heinemann, 1899.
- ^ C. H. Bothamley, Ilford Manual of Photography, London: Britannia Works Co. Ltd., 1891.
- ^ John A. Hodges, Photographic Lenses: How to Choose, and How to Use, Bradford: Percy Lund & Co., 1895.
- ^ C. Welborne Piper, A First Book of the Lens: An Elementary Treatise on the Action and Use of the Photographic Lens, London: Hazell, Watson, and Viney, Ltd., 1901.
- ^ Conrad Beck and Herbert Andrews, Photographic Lenses: A Simple Treatise, second edition, London: R. & J. Beck Ltd., c. 1902.
- ^ חיפוש בגוגל
- ^ Ives, Herbert Eugene (1920). Airplane Photography (Google). Philadelphia: J. B. Lippincott. p. 61. ISBN 9780598722225. נבדק ב-12 במרץ 2007.
{{cite book}}: (עזרה) - ^ Mees, Charles Edward Kenneth (1920). The Fundamentals of Photography. Eastman Kodak. p. 28. נבדק ב-12 במרץ 2007.
{{cite book}}: (עזרה) - ^ Derr, Louis (1906). Photography for Students of Physics and Chemistry (Google). London: Macmillan. p. 83. נבדק ב-12 במרץ 2007.
{{cite book}}: (עזרה)























































































