פונקציית הערך השלם

בערך זה
נעשה שימוש
בסימנים מוסכמים
מתחום המתמטיקה.
להבהרת הסימנים
ראו סימון מתמטי.

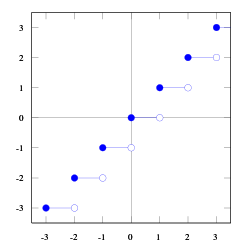
במתמטיקה, פונקציית הערך השלם (נקראת גם פונקציית רִצפה) היא פונקציה המחזירה לכל מספר ממשי x את המספר השלם הגדול ביותר שקטן או שווה ל-x (מעגלת כלפי מטה). פונקציה זו מסומנת $\lfloor x\rfloor$ , $\ [x]$ או (x)‏floor. דוגמאות: $\lfloor 2.7\rfloor =2$ , $\lfloor -2.1\rfloor =-3$ , $\lfloor -2\rfloor =-2$ .

סימון

פונקציית הערך השלם הוגדרה לראשונה בשנת 1798 על ידי המתמטיקאי הצרפתי אדריאן-מארי לז'נדר, בהוכחתו לנוסחת לז'נדר. קרל פרידריך גאוס הציג את הסימון $\ [x]$ בהוכחתו השלישית, משנת 1808, למשפט ההדדיות הריבועית. זה נותר הסימון המקובל עד שבשנת 1962 הציג קנת אייברסון, בספרו A Programming Language (על שפת התכנות APL), את הסימון $\lfloor x\rfloor$ ואת השם "רצפה" (floor) לפונקציה זו (ולצדם את הסימון $\lceil x\rceil$ והשם "תקרה" לפונקציית תקרה). מאז מקובלים הסימונים של גאוס ושל אייברסון. יש המשתמשים לפונקציית הערך השלם בסימון $[[x]]$ .^[1]

תכונות

לכל x ממשי הפונקציה מקיימת:

\lfloor x\rfloor \leq x<\lfloor x\rfloor +1

כאשר השוויון באגף שמאל מתקיים אם ורק אם x שלם.

הפונקציה היא אידמפוטנטית: $\lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor$
לכל x ממשי ולכל n שלם מתקיים:

\lfloor x+n\rfloor =\lfloor x\rfloor +n

עיגול למספר השלם הקרוב ביותר ל-x ניתן על ידי הנוסחה $\lfloor x+0.5\rfloor$ .

פונקציות דומות

פונקציית תקרה

ערך מורחב – פונקציית תקרה

פונקציית התקרה מחזירה לכל מספר ממשי x את המספר השלם הקטן ביותר שגדול או שווה ל-x. הפונקציה מסומנת $\lceil x\rceil$ או (x)‏ceiling. ניתן לתאר את פונקציה התקרה כך:

\lceil x\rceil =\min \,\{n\in \mathbb {Z} \mid n\geq x\}

דוגמאות: $\lceil 2.7\rceil =3$ , $\lceil -2.1\rceil =-2$ , $\lceil -2\rceil =-2$ .

הקשר בין פונקציית הרצפה לבין פונקציית התקרה ניתן על ידי הנוסחה $\lceil x\rceil =-\lfloor -x\rfloor$ .

לכל k שלם מתקיים: $\lfloor k\rfloor =\lceil k\rceil =\lfloor k/2\rfloor +\lceil k/2\rceil =k$

לכל k מספר ממשי מתקיים: $\lfloor k\rfloor \leq k\leq \lceil k\rceil$ .

פונקציית Trunc

ערך מורחב – פונקציית קיטום

במדעי המחשב מוכרת פונקציה בשם Trunc, קיצור של Truncate. רמז לתיאור הציורי שלה כפונקציה שלוקחת מספר ממשי ו"מקצצת" את החלק השברי שלו ומשאירה רק את החלק השלם. פונקציה זו מתנהגת כמו פונקציית רצפה עבור מספרים חיוביים, וכפונקציית תקרה עבור שליליים. שלוש הפונקציות מקבלות ערך שווה עבור כל המספרים השלמים.

מוגדרות היטב

פונקציית הערך השלם (פונקציית הרצפה) מוגדרת היטב, במובן שלכל $x$ ממשי אכן קיים מספר שלם $n$ גדול ביותר שמקיים $n\leq x$ (ואז נוכל להגדיר $\lfloor x\rfloor :=n$ ). הקיום של מספר שלם כזה $n$ נובע משילוב של שתי תכונות של קבוצת המספרים השלמים: ראשית, הקבוצה הזו אינה חסומה מלמטה, ושנית, בכל תת-קבוצה חסומה מלמעלה של מספרים שלמים יש איבר גדול ביותר. לכן, התכונה הראשונה מובילה לכך שהקבוצה $A:=\{n\in \mathbb {Z} :n\leq x\}$ של כל המספרים השלמים שקטנים או שווים ל $x$ היא קבוצה לא ריקה, והתכונה השנייה מובילה לכך שיש בקבוצה $A$ איבר גדול ביותר. האיבר הזה הוא בדיוק הערך השלם של $x$ . באופן דומה ניתן להראות שפונקציית התקרה מוגדרת היטב, בהתבסס על כך שקבוצת המספרים השלמים אינה חסומה מלמעלה, ובכל תת-קבוצה חסומה מלמטה של מספרים שלמים יש איבר קטן ביותר.