חיבור בטור ובמקביל
במעגל חשמלי, חיבור הרכיבים יכול להתבצע באינספור דרכים שונות. הדרכים הפשוטות ביותר הן חיבור בטור או חיבור במקביל. בחיבור בטור כל הרכיבים מקבלים אותו זרם חשמלי, ולעומת זאת, בחיבור במקביל כל הרכיבים מקבלים אותו מתח חשמלי.
את המתח והזרם במעגל מחשבים בדרך כלל דרך רכיב שקול, שהוא רכיב שיכול להחליף כמה אחרים יחד, תוך שהמעגל כולו נשאר זהה. החוקים המשמשים לחישוב המתח, הזרם והרכיב השקול, נובעים מחוקי קירכהוף למעגלים חשמליים.
ברכיבים פשוטים כגון נגד, סליל השראה, קבל או מקור מתח, יש שתי אפשרויות לחוקי החיבור: הרכיב השקול שווה לסכום ערכם של הרכיבים, או שווה להופכי של סכום אחד חלקי הערכים הבודדים (ראו בהמשך). אם הערכים מחוברים בהופכי, הערך השקול קטן מערך כל הערכים הבודדים, בניגוד לחיבור ערכים שבו הערך השקול גדול מכל אחד מהערכים הבודדים. לדוגמה, עבור נגדים המחוברים במקביל, הנגד השקול יהיה קטן מכל אחד מהנגדים הבודדים.
חוקים נוספים:
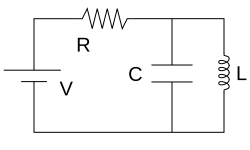
- במעגל מורכב יותר, שאינו כולו בטור או במקביל, ניתן לעיתים לבנות בשלבים את הרכיב השקול: לדוגמה באיור למעלה, הקבל והסליל מחוברים במקביל זה לזה, ושניהם יחד מחוברים בטור לנגד ולמקור המתח.
- במעגל שבו שני רכיבים בלבד, הם מחוברים גם בטור וגם במקביל.
- קיימים גם מעגלים חשמליים שלא ניתנים לפירוק בטור ובמקביל. גשר ויטסטון הוא דוגמה למעגל פשוט מסוג זה.
בתחומי פיזיקה אחרים גם ניתן לחבר במקביל או בטור אלמנטים, לדוגמה קפיצים במכניקה, או צינורות בזרימה.
מעגל טורי
[עריכת קוד מקור | עריכה]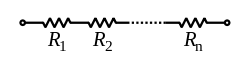

בחיבור טורי הזרם בכל האלמנטים שווה, והמתח הכולל בהדקים הקיצוניים שווה לסכום המתחים על כל אלמנט בנפרד. מתוך שיקולים אלה ניתן לחשב את האלמנט השקול עבור סוגים שונים של רכיבים.
דוגמה למעגל טורי: 4 סוללות של 1.5 וולט המחוברות בטור, ויחד נותנות מתח של 6 וולט. דוגמה נוספת: 10 נורות קטנות המחוברות בשרשרת - המתח על כל נורה יהיה 220 וולט חלקי 10, כלומר 22 וולט, והזרם בכולן יהיה שווה.
כאשר מספר רכיבים מחוברים בטור, נתק בכל אחד מהם יגרום לנתק בכולם. לדוגמה: אם כמה נורות מחוברות בטור, ואחת מהן נשרפת, כולן מפסיקות לפעול (אבל לא נשרפות).
בחיבור נגדים בטור, ההתנגדות השקולה שווה לסכום ההתנגדויות הבודדות[1]:
בחיבור משרנים בטור, ההשראות השקולה שווה לסכום ההשראויות הבודדות:
בחיבור מקורות מתח בטור, המתח השקול שווה לסכום המתחים הבודדים, אך צריך לחבר או להחסיר על פי כוון המתח.
בחיבור קבלים בטור, הקיבול השקול שווה להופכי של סכום ההופכיים של הקיבולים הבודדים[2]:
- .
מעגל מקבילי
[עריכת קוד מקור | עריכה]

בחיבור מקבילי המתח על כל האלמנטים שווה, והזרם הכולל בהדקים הקיצוניים שווה לסכום הזרמים בכל אלמנט בנפרד. מתוך שיקולים אלה ניתן לחשב את האלמנט השקול עבור סוגים שונים של רכיבים.
דוגמה למעגל מקבילי: מערכת החשמל בבית פרטי בנויה באופן מקבילי, כך שכל השקעים מקבלים מתח 220 וולט ישירות מרשת החשמל. הזרם שרושם מד-הזרם בבית מתחלק על כל הצרכנים (מכשירי החשמל) בבית.
במעגל מקבילי קצר של אחד הרכיבים יגרום לקצר בכל המעגל. לדוגמה: במעגל בבית, קצר בקומקום החשמלי (או בכל מכשיר אחר) יגרום לקפיצת המאמ"ת (מפסק אוטומטי מגנטי תרמי) בלוח החשמל. אם היה קצר להארקה יופעל מפסק פחת, מכיוון נוצרת זליגת זרם להארקה מצב המדמה התחשמלות.
בחיבור קבלים במקביל, הקיבול השקול שווה לסכום הקיבולים הבודדים[3]:
- .
בחיבור נגדים במקביל, ההתנגדות השקולה שווה להופכי של סכום אחד חלקי ההתנגדויות הבודדות[4]:
- .
בחיבור משרנים במקביל, ההשראות השקולה שווה להופכי של סכום אחד חלקי ההשראויות הבודדות:
- .
חיבור מקורות מתח במקביל לא אמור להתבצע שכן הוא יגרום לפריקה של אחד מהם. אפשר למצוא רכיב שקול למעגל שבו מקורות מחוברים במקביל רק כאשר יש גם התנגדויות למקורות, כלומר נוסף נגד למעגל.
רכיבים אחרים
[עריכת קוד מקור | עריכה]חיבורים בטור ובמקביל של רכיבים חשמליים אחרים, יכולים לתת תוצאות נוספות בעלות שימושים.
- מקורות מתח - חיבורם בטור שקול למקור מתח אחד בעל סכום המתחים.
- מקורות זרם - חיבורם במקביל שקול למקור זרם אחד בעל סכום הזרמים.
- מתגים חשמליים - חיבורם במקביל מממש שער לוגי מסוג OR, וחיבורם בטור מממש שער לוגי מסוג AND. כיום מתגים ממומשים לרוב באמצעות טרנזיסטורים, וחיבורם באופן כזה מהווה טכניקה יסודית בבנייתם של מעבד ומחשב.
ראו גם
[עריכת קוד מקור | עריכה]קישורים חיצוניים
[עריכת קוד מקור | עריכה]הערות שוליים
[עריכת קוד מקור | עריכה]- ^ ההוכחה לכך היא שלפי חוק אוהם (המתח חלקי הזרם), ומכיוון שבטור הזרם שווה על כל אחד מהנגדים והמתח מתחלק ביניהם יוצא ש:
- ^ ההוכחה לכך היא שלפי הגדרת הקיבול (המטען החשמלי על הקבל חלקי המתח עליו), ומכיוון שבטור הזרם שווה על כל אחד מהנגדים וכמוהו גם המטען החשמלי שמושפע מהזרם, ואילו המתח מתחלק ביניהם יוצא ש:
- ^ ההוכחה לכך היא שלפי הגדרת הקיבול (המטען החשמלי על הקבל חלקי המתח עליו), ומכיוון שבמקביל הזרם מתפצל בין הקבלים וכמוהו גם המטען החשמלי שמושפע מהזרם, ואילו המתח שווה על כל אחד מהם יוצא ש:
- ^ ההוכחה לכך היא שלפי חוק אוהם (המתח חלקי הזרם), ומכיוון שבמקביל המתח שווה על כל אחד מהנגדים והזרם מתפצל ביניהם יוצא ש:












